モンティホール問題の解説で扉を増やすな
はじめに
モンティホール問題とは
プレーヤーの前に3つのドアがあって、1つのドアの後ろには当たりとしてヤギが、残りの2つのドアはハズレである。プレーヤーが1つドアを選択した後、司会のモンティが残りのドアのうちハズレのドアを開けて見せる。
ここでプレーヤーは、最初に選んだドアから残っている開けられていないドアに変更してもよいと言われる。プレーヤーはドアを変更すべきだろうか?
この場合ヤギがいるCのドアが当たりです

プレイヤーがドアを選ぶと

ハズレのドアが開かれ、ハズレであることが示されます

この時「選んだドアを変えてもいいですよ」と言われた場合、
プレイヤーは選んだドアを変えるべき?

というのがモンティ・ホール問題、モンティ・ホール・ジレンマ、モンティ・ホール・パラドックス
と呼ばれる問題です
直感的には
- 「どちらを選んでも変わらない」
- 確率が
1/3 1/2
といった解答がよくなされるが、いずれも間違いです
実際には
- 確率は
1/3 2/3
が正解であり
こういった直感と実際の数値の乖離からパラドックスなどと呼ばれるわけです
課題
このパラドックスを解消する方法として、
ドアが100個ある場合を考えてみましょう!
という説明がよくなされています
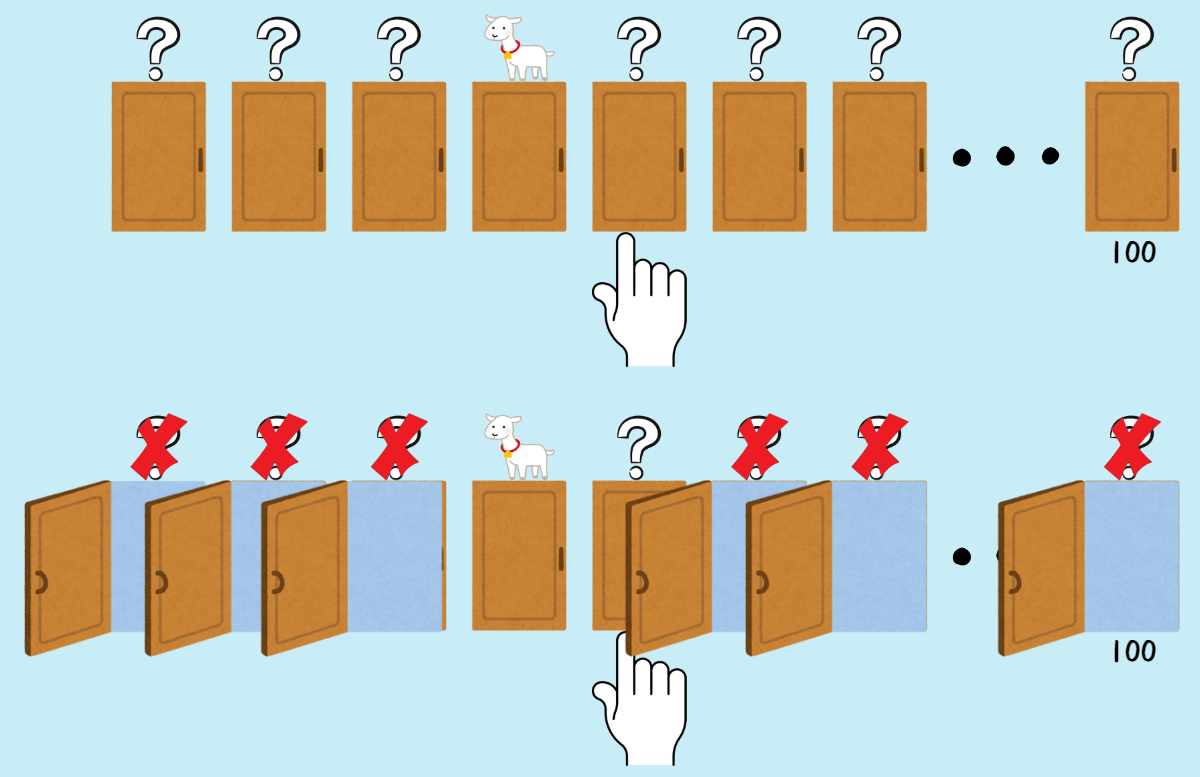
100個あるうちのハズレが98個開けられたら
どう考えても変えた方が良いって分かりますよね?!という説明です
確かにこの場合、変えた方が良さそうというのは直感的に分かるのですが、
ドアが2つの場合と100個の場合が同じ問題であるというのが全く直感的ではない
この説明が最も分かり易い説明かのように世にはびこっていることが許しがたい
解決
この問題に対する最も簡単で直感的な説明方法は
ドアを変更したときに損をするのは、初めに当たりを引いていた時だけ
これ以外にないです
以上
補足
いちおう補足しておくと、
最初に当たりを選んでいる確率は
最初にハズレを選んでいる確率は
残ったハズレを司会者が開いた後、ドアを変更した場合
結果的にハズレを選んでいる確率は、最初に当たりを選んでいた場合で
結果的に当たりを選んでいる確率は、最初にハズレを選んでいた場合で
なぜこんなシンプルなことを説明するためにドアを100個にする必要があるのか
さいごに
全然Tech系の記事じゃなくなってしまった
ダメかな…ダメだったらどこか別のところに……
Discussion
モンティホール問題については、こういう間違いだらけの説明が横行していて呆れる。
初めに当たりを引いている確率は1/3だから変更すべきと説明しているけど、最初の時点では残りの2つの扉のどちらも当たっている確率は1/3。だから、そんなのは説明になっていない。
最初の時点では残りの2つの扉のそれぞれが当たっている確率が1/3ずつである事は、説明になっていない事を説明できていないように感じました。
ちなみに私の説明ならこうなります。
3つの扉のそれぞれは 1/3 ずつ当たる確率を持っている。
最初に選んだ扉は 1/3 の確率で当たる。
残った二つの扉もそれぞれ 1/3 ずつの確率を持っているので二つ合わせると 2/3 の当たる確率を持っている。
(途中確認: つまり、最初に選んだ扉が外れである確率が 2/3 であるという事)
全体で 2/3 の確率を持っている二つの扉のうち、外れている片方を司会者が潰してくれるので、残った片方は 2/3 の確率で当たる可能性がある扉になるし、
この時に「全体で 2/3 の可能性を持っている二つのうちの絶対に外れている片方を潰す」話に関係してこない最初に選んだ扉の確率は変動しない。
この結果、最初に選んだ扉(1/3の確率で当たる扉)と残った扉(2/3の確率で当たる扉)のどちらを選ぶかという問題を出題されている事になり、選択を維持する時の勝率が 1/3 で、選択を変更する時の勝率が 2/3 になる。
私がモンティホール問題をコードで実装してどうやら実際に正しいらしいと確認した時の最大の疑問が、「なんで潰された 1/3 の確率が残り二つに等しく流入してそれぞれが 1/2 ずつにならないのか?」でした。
今、当時の自分に回答するなら『2/3 の確率を持っている二つの扉の中で話が完結しているから、関係ない最初に選んだ扉の確率は変動しない。』となると思います。
方針は近いですが、より丁寧に説明されていてかつ分かりやすさは損ねていない、とても良い説明だと思います
コメントありがとうございます
この説明が最も分かり易い説明かのように世にはびこっていることが許しがたい
とあなたの文をそのままコピペしました
分かりやすいも何も違いますので
他の方のコメントを見てもなお、気がつけない、それがモンティホール問題の面白いところです