Zenn
👻

連結リストの後半分を逆順にする方法

2024/04/05に公開
アルゴリズム
#
アルゴリズムとデータ構造
#
連結リスト
tech

問題文

下記はマサチューセッツ工科大学オープンコースウェア（MIT OCW）2010年度の「計算機科学のための数学」に出題する問題の要約：

近くの学校の生徒がアイスクリームトラックに殺到する。
一台では追いつけないため、生徒の列の最後にもう一台のトラックがくる。
だが、生徒たちは納得が行かない：これでは一番遅かった人が先にアイスクリームをもらう！
代わりに、列の後半に立つ生徒はみんな逆順になればいいと決断される。

「生徒を表す長さ2nの連結リストの後半分（n+1番目から）を逆順にせよ」と。

第一候補者

リストを最後まで渡り、それぞれn番目要素にN、n+1番目にP、そして最後の要素にlastポインターを設置する（lastはこのステップでしか使用しない）：

P以降のリストを真逆にする：

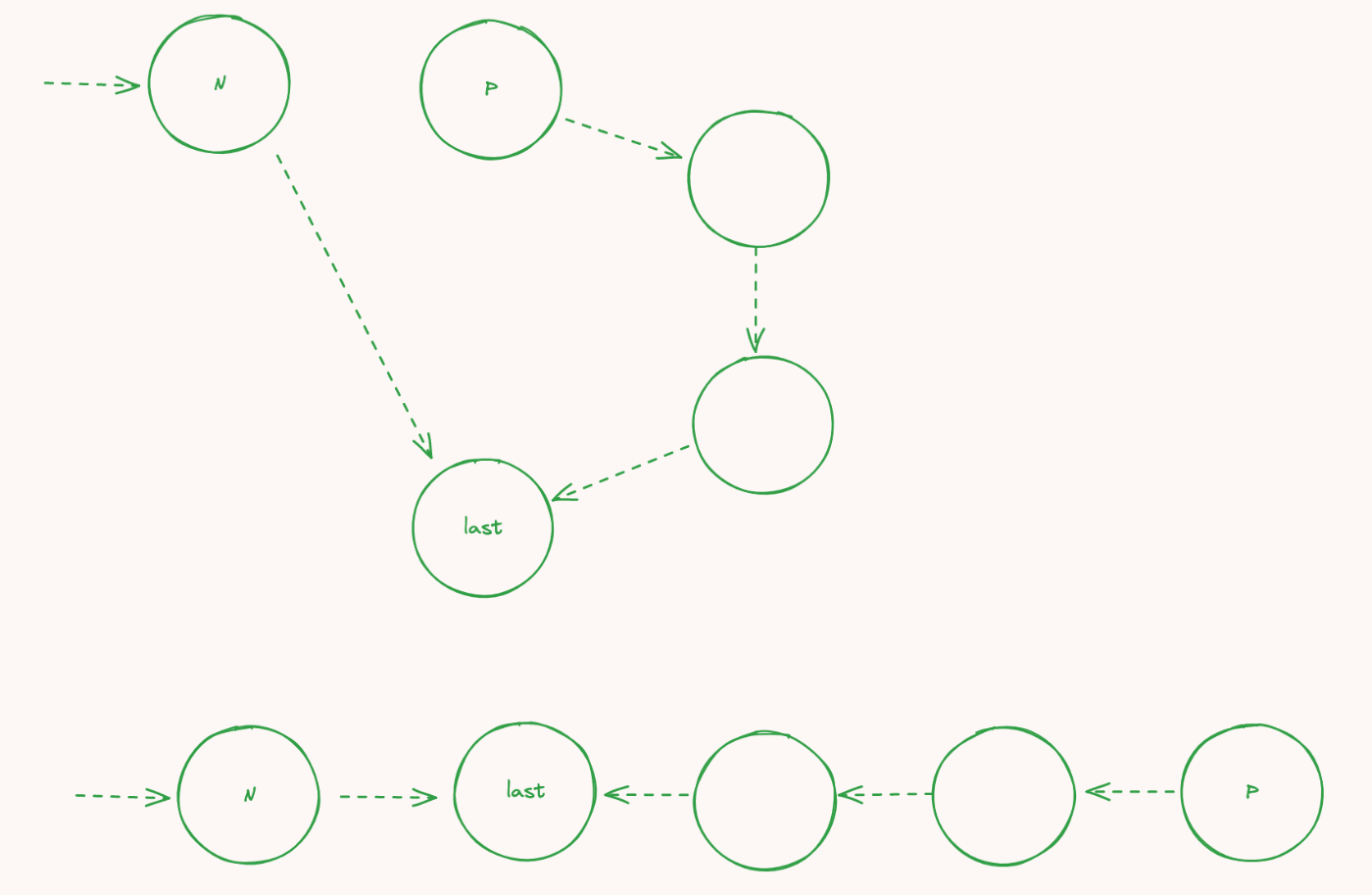
これでリストの後半分の順番は一見正しく見えるが、逆方向になっているのでこれではリストがlastで終わってしまう。

今度はPを使って連結方向を正す。

  1. まず、Pの後ろにくる要素への参照をP2に保存する：

  1. P2からPを参照：

  1. PからP2へのポインターを削除：

  1. PをP2にする：

ご覧の通り、最後の要素二つの方向の修正が完成した。同じ手順を次の要素に適用すれば正解が出るわけだが、ちょっとした問題点がある：ステップ２〜４でP2は同時にPと次の要素を指している。つまり、P2に二つ目のポインターを与えないといけない。

また、リストの後半分を二度も通ってしまう。

というわけで、より適切なアルゴリズムを見てみよう。

第二候補者

元のリスト：

「❌」は最後のnullノードを表す。

  1. まずn+1目要素への参照をPに代入する：

このPは一回しか代入しないので、これからNからだんだん離れていく。

  1. 次にn+1目要素へのポインタP2を作成。

Pと違ってP2いつもn+1目要素に割り当てていく。

  1. Nの次を1にする：

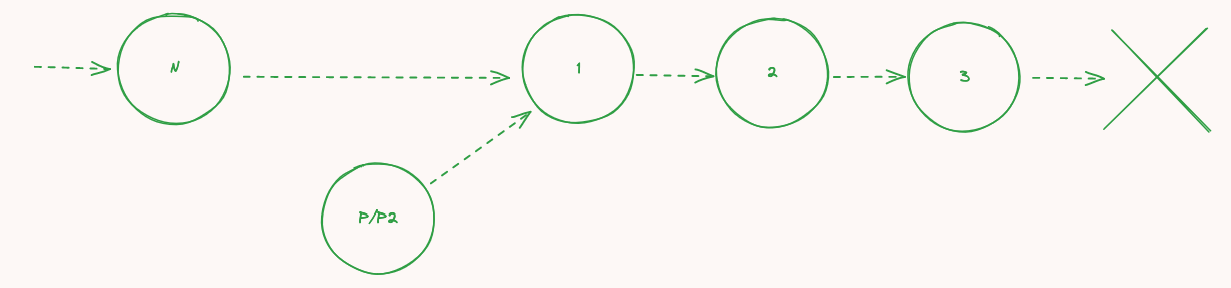
  1. Pの指しているノードの次を2にする：

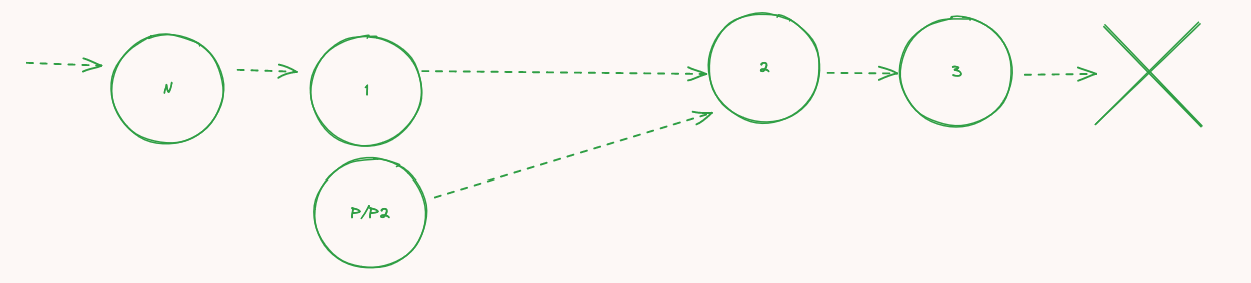
お気づきかと思いますが、「PとP2の次」ではなく、「Pの次」ですね。今、PとP2はたまたま一致しているわけだが、この状況は長く続かない。

  1. では、1の次をP2（Pではなく）にする：

そしてP2をn+1目要素にリセットする：

同じステップを繰り返すと：

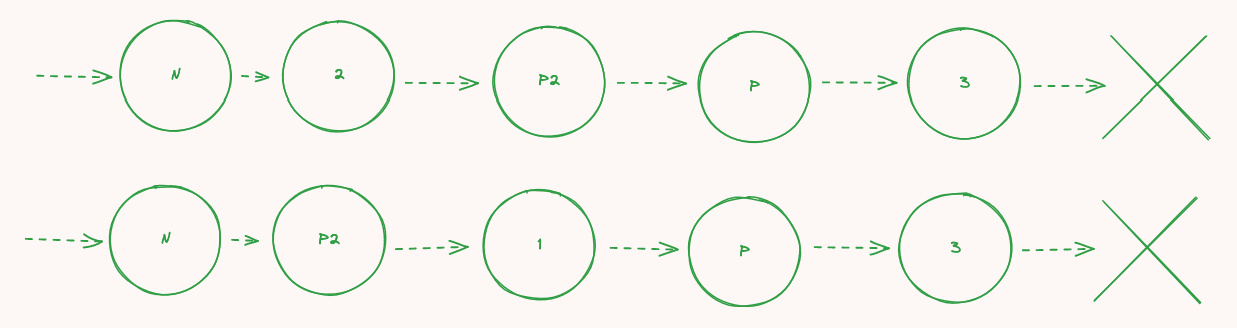
もう一回：

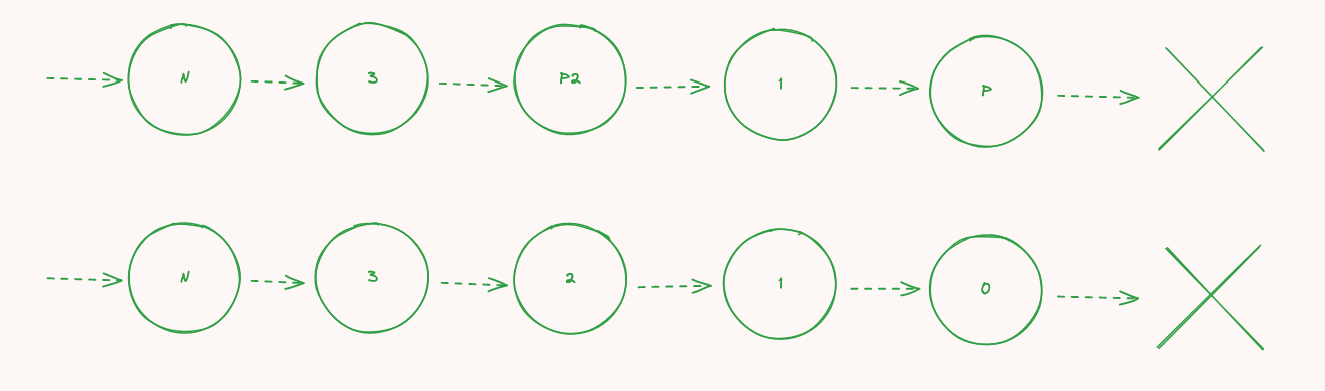
完成です。

比較

１番目：

  • リストの最後までいく：2n
  • n回：
    • P2作成
    • P2からPへの追加ポインタ
    • PからP2へのポインタ削除
    • P2をPに代入

合計：2n + 4n = 6n

２番目：

  • n番目までいく：n
  • n回：
    • P2作成
    • Nの次を変更
    • Pの次を変更
    • n+1の次をP2にする

合計：n + 4n = 5n

結論

二番目の方はちょっと早いかな。漸近式はいずれもO(n)だが、CPUサイクル数はどうだろう。

Discussion