diffコマンドのしくみ、知っていますか？

diffコマンドのしくみ、知っていますか？

はじめに

こんにちは。株式会社Elithの松山です。ElithではMachine Learning Research Engineerとして、お客様の課題をAIを駆使して解決しています。

ところでみなさん、「Git」を使いこなしていますか？私もさらなる理解を目指して、最近改めて勉強しています。普段何気なく使っているコマンドですが、その仕組みまで把握できている人は少ないのではないでしょうか。

そんな中、弊社CTO井上が書いた「実務レベルでわかる/使いこなせるようになるGit入門コマンドライン演習80」が非常に参考になります。この本を通じて、Gitコマンドの奥深い仕組みを学ぶことができました。

今回は、特にLinux/Gitのdiffコマンドについて、その仕組みを深掘りしていきたいと思います。

本記事内で使用している図は参考文献の論文から引用しています。

diffコマンドとは

diffコマンドは、Unix系オペレーティングシステムで広く使われているツールで、2つのテキストファイルを比較し、その違いを表示するものです。開発者にとっては、バージョン管理システムの一環として、変更点を確認するために非常に重要なコマンドです。

例えば、ソフトウェア開発において、あるファイルの異なるバージョンを比較することで、どの部分が変更されたのかを把握できます。このコマンドは、プログラムのデバッグや、共同開発の際の変更履歴の確認など、多岐にわたる用途で使用されます。

Gitでのdiff

Gitにもdiff コマンドは存在します。ファイル間の差分を確認するのはもちろん様々な状況下で差分を確認できます。

• コミット間の差分確認: Gitでは、2つのコミット間の差分を確認するためにgit diffを使用します。これにより、どのファイルがどのように変更されたかを詳細に把握できます。

  git diff commit1 commit2
  

• ワーキングディレクトリとインデックスの差分確認: ワーキングディレクトリ内で行われた変更と、インデックス（ステージングエリア）にある変更の差分を確認することもできます。

  git diff
  

• 特定のブランチ間の差分確認: ブランチ間の差分を確認することで、異なる作業ブランチがどのように分岐しているか、どの部分が異なるかを理解できます。

  git diff branch1 branch2
  

Gitでのdiffコマンドは、開発者がコードの変更を追跡し、レビューし、マージする際に不可欠なツールです。視覚的な差分表示やパッチファイルの生成など、多様な機能を持つため、効率的なコード管理をサポートします。

以下、文書間の差分を表示する役割のdiffコマンドに注目します。

diffコマンドの仕組み

diffコマンドは、2つのテキストファイルを比較し、違いを表示するツールです。この機能を実現するために、diffは主に2つのアルゴリズム的概念を利用しています。それが、LCS（Longest Common Subsequence）とSES（Shortest Edit Script）です。

LCS（Longest Common Subsequence）

LCSとは、2つのシーケンスの中で最も長い共通の部分シーケンスのことを指します。ここでシーケンスとは、文字列やリストなどを指します。また、部分シーケンスとは、元のシーケンスからいくつかの要素を削除したもので、残った要素の順序は元のシーケンスと同じである必要があります。LCSは、2つのシーケンスがどれだけ似ているかを測る指標として使われます。

例えば、"ABCBDAB"と"BDCAB"は、"AB"や"BB"を部分列として持ちます。両文字列に共通する部分文字列に"BCAB"があり、これが最長であるためLCSとなります。

"AB"：ABCBDAB、BDCAB
"BB"：ABCBDAB、BDCAB
"BCAB"：ABCBDAB、BDCAB

SES（Shortest Edit Script）

SESは、1つのシーケンスを別のシーケンスに変換するための最短編集スクリプトのことです。編集操作には、挿入、削除、置換の3つがあり、SESはこれらの操作の最小回数で変換を行う方法を示します。挿入はシーケンスの任意の位置に1つ要素を追加する、削除はシーケンスの任意の要素を1つ取り除く、置換はシーケンスのある1つの要素を別の要素に変える操作です。diffコマンドは、実際にはこのSESを計算して、2つのファイル間の違いを表示します。

SESはLCSを用いて計算できます。

ABCBDAB
→ BCBDAB　：A削除
→ BDCBDAB　：D追加
→ BDCDAB　：B削除
→ BDCAB　　：D削除

LCSの簡単な計算方法

LCSを計算するための基本的な方法は、動的計画法（Dynamic Programming, DP）です。この方法を使うことで、2つのシーケンス間のLCSを効率的に見つけることができます。

動的計画法(DP)

動的計画法は、問題をいくつかの部分問題に分割し、それらを解くことで全体の問題を解決する手法です。LCSの計算においては、次のようなDPテーブルを構築します。

1. 2次元配列dpを用意し、dp[i][j]をシーケンスAの先頭からi番目までとシーケンスBの先頭からj番目までのLCSの長さとする。
2. 初期条件として、dp[0][j] = 0およびdp[i][0] = 0とする。
3. 2つのシーケンスの要素を順に比較し、要素が一致する場合は、dp[i][j] = dp[i-1][j-1] + 1とする。要素が一致しない場合は、dp[i][j] = max(dp[i-1][j], dp[i][j-1])とする。

このようにしてDPテーブルを埋めることで、LCSの長さを求めることができます。

LCSの計算例

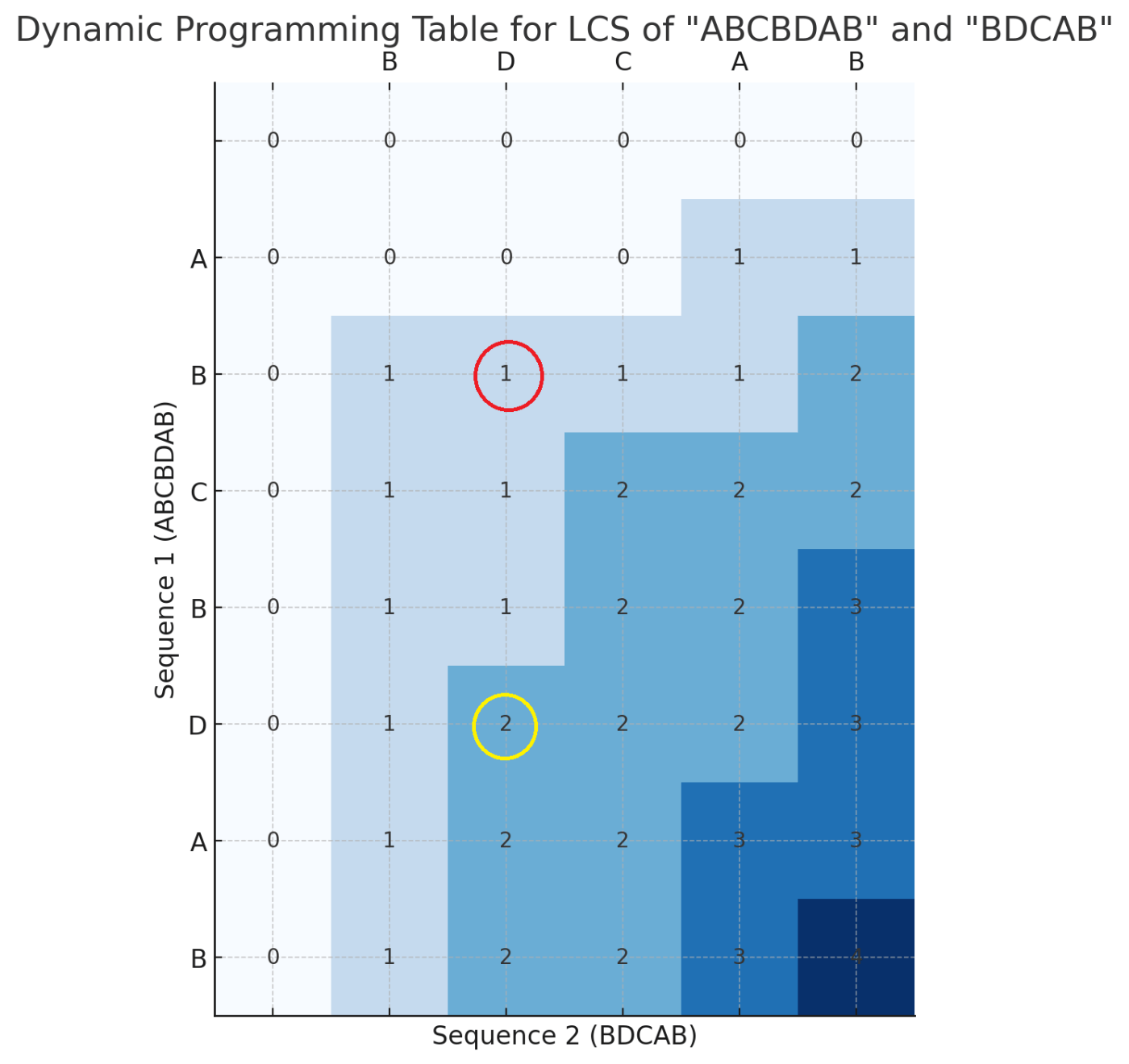
"ABCBDAB"と"BDCAB"のLCSを動的計画法で計算します。

まず、DP配列を用意します。7文字と5文字のLCSを求めるので、8×6のサイズの配列で十分です。

そして、配列の0行目と0列目を0に初期化します。これは、"ABCBDAB"の0文字目まで、すなわち空文字と"BDCAB"が共有する部分列は空文字しかないためです。

あとは、左上から配列を埋めていきます。赤丸の地点では、上と左が0と1であるので、大きい1を入れます。黄丸の部分は、"ABCBDAB"と"BDCAB"のDの部分に対応するため、左上のマスのLCSである"B"に"D"を追加でき、LCSは"BD"、LCS長は2となります。

実際の計算方法

動的計画法では、時間計算量は$O(|S|\cdot|T|)$となります。このため、ファイルの大きさが大きくなると実行に多くの時間がかかります。また、ファイル間の違いが少ない場合でも、$O(|S|\cdot|T|)$の時間がかかってしまいます。

そのため、diffコマンドにはより効率的なアルゴリズムが使用されることが多いです。その一つのアプローチとして、グラフ理論を用いたアルゴリズムがあります。

グラフ理論の適用

本アルゴリズムでは、LCSの問題をグラフ上の最短経路問題として捉えます。具体的には、シーケンス$S$と$T$の比較を以下のようにモデル化します。

edit graph

1. グラフの頂点数は、$(|S|+1)\cdot(|T|+1)$個あります。
2. 各頂点$(i,j)$から、次の頂点にコスト1の辺を張ります。
   • $(i+1,j)$
   • $(i,j+1)$
   • $(i+1,j+1)$（$S_{i+1}=T_{j+1}$の場合）

このグラフ上で、$(0,0)$から$(|S|,|T|)$への最短路を求めることで、$S$と$T$のLCS,SESを求めることができます。

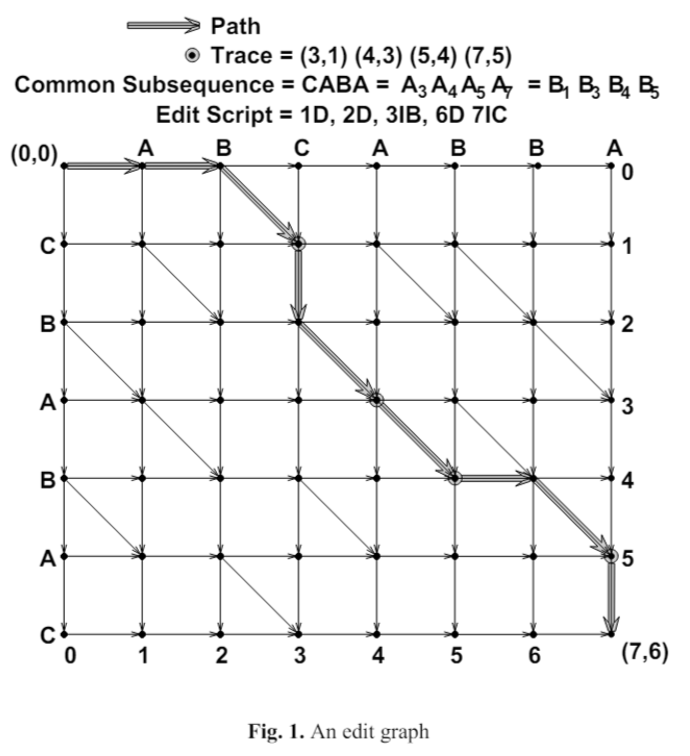
最短路の計算

単純に幅優先探索などを用いてこのグラフの最短路を求めると、時間計算量は$\Theta(|S|\cdot|T|)$となります。しかし、本アルゴリズムでは、DPを工夫してグラフを明示的に持たずに計算を行います。これにより、計算時間は$\Theta((|S|+|T|)\cdot\delta(S,T))$に短縮されます。ここで$\delta(S,T)$とはSESの長さです。すなわち、2ファイルの差分が小さいとき、先述の動的計画法よりも高速にLCSを計算できます。

DPの工夫

D-path

• D-pathは、edit graphにおける始点$(0,0)$から始まり、辺の重みの総和が$D$になるパスです。これは「共通でない文字を選んだ回数が$D$」や「edit scriptの長さが$D$」であるパスと解釈できます。

(D,k)-furthest path

• D-pathのうち、終端$(i,j)$が$k$-diagonalにあり、$i$が最大のものを(D,k)-furthest pathと呼びます。最小の$D$で(D,|T|−|S|)-furthest pathの終端が$(|S|,|T|)$になるときの$D$が$\delta(S,T)$です。
• 頂点 $(i,j)\in V$ のうち $j-i=k$ $(-|S|\leq k\leq |T|)$ を満たす部分集合を $k$-diagonal と呼びます。

注目ポイント

• (0,0)-furthest pathは、lcp(S,T)回だけ斜めの辺を辿り、終端は$(lcp(S,T), lcp(S,T))$です。
  • lcp(S,T)：文字列$S$, $T$に共通する最長の接頭辞の長さ
• (D,k)-furthest path($D>0$)は、以下の2つのパスのいずれかから得られます:
  • (D−1,k−1)-furthest pathから右向きの辺を1回辿り、そこからlcp(S[i…],T[j…])回だけ斜めの辺を辿ったパス
    • lcp(S,T)：文字列$S$, $T$に共通する最長の接頭辞の長さ
  • (D−1,k+1)-furthest pathから下向きの辺を1回辿り、そこからlcp(S[i…],T[j…])回だけ斜めの辺を辿ったパス
• よって|S|と|T|についての2重ループだったDPを、 D と k についての2重ループのDPとしてみることができるようになります！

疑似コード

For D ← 0 to S+T Do
  For k ← −D to D Do
    Find the endpoint of the furthest reaching D-path in diagonal k from DP[D-1][k-1] and DP[D-1][k+1].
    If (S,T) is the endpoint Then
      The D-path is an optimal solution.
      Stop

更なる高速化手法

さらに、高速化のためにサフィックスツリーやRMQ（Range Minimum Query）を活用することで、計算時間を$\Theta((|S|+|T|)\log(|S|+|T|)+\delta(S,T)^2)$に短縮できることが知られています。本稿では、長くなるため詳細は割愛します。

まとめ

diffコマンドは、LCS（Longest Common Subsequence）を用いたSES（Shortest Edit Script）の計算によって実現されています。

LCSは動的計画法を用いて計算できますが、実際にはグラフ理論を用いた、より効率的なアルゴリズムが使用されています。

動的計画法などの数理最適化の分野には、一般の人から見ると天才的な工夫が多く見られます。しかし、これらの工夫も経験豊富な専門家からすれば、ある種の一定の思考ルーチンから生み出されたものにすぎないでしょう。たくさんの論文やアイデアに触れることで、そうした思考力を身につけていきたいと強く感じています。

最後に宣伝となりますが、株式会社Elithは最先端のAI技術をビジネスに実装し、価値を生み出すテックカンパニーです。最近ではLLMの活用に関してさまざまな取り組みをしており、多数のイベントにも登壇しています。少しでも興味がある方は、X(旧Twitter)経由やElithのWebページ経由で、ぜひ気軽にお話を聞きにきてください。

参考文献

• An O(ND) Difference Algorithm and Its Variations (1986) - Eugene W. Myers