Information Retrieval | 06 Scoring, Term Weighting, and the Vector...
Scoring, term weighting and the vector space model
- 備忘:最終目的はクエリ用語と関連の強い文書を検索すること
-
クエリにマッチする文書をランク付けすることが必要
- 大規模な文書コレクションの場合、マッチする文書の数が大量となる。
- 検索エンジンはマッチする文書ごとに、手元のクエリに対するスコアを計算する。
- スコアが高い文書ほど、クエリ(=ユーザーが求める情報)にマッチする可能性が高い。
- このチャプターでは、クエリと文書のペアにスコアを割り当てる方法を整理
3つの主要なアイデア
- パラメトリックインデックスとゾーンインデックス
- パラメトリックインデックス:文書が記述されている言語などのメタデータによってインデックスを作成し文書を検索。
- ゾーンインデックス:クエリに応答して文書をスコアリング(それによってランキングする)
- 特定のクエリ用語がマッチング文書の特定の領域に出現するクエリを考える
- 用語の出現統計に基づいて、文書中の用語の重要度に重み付け
- フリーテキストクエリ:クエリ用語の相対的な順序、重要度、文書のどこに含まれるかを指定しない。関連する情報を幅広く収集できる。
- ベクトル空間スコアリング
- 各文書を重みのベクトルとみなすことで、クエリと各文書の間のスコアを計算
その他
- ベクトル空間モデルのための用語重み付けの方法にはいくつか種類がある。
- 第7章では、ベクトル空間スコアリングの計算的側面と関連するトピックを展開(次回以降に説明)。
Parametric and zone indexes
-
パラメトリックインデックス
- 文書のメタデータ毎にインデックスを作成し文書を検索。
- 辞書は固定された語彙から構成される。固定された集合。
- メタデータの例:言語、タイトル、著者、発行年
-
ゾーンインデックス
- 文書の特定のゾーン(=領域)毎にインデックスを作成し文書を検索。
- 特定のクエリ用語がマッチング文書の特定の領域(=ゾーン)に出現するかを判定して検索する。
- 辞書は限定されない量のテキストから構成される
- ゾーンの例:タイトル、著者、章の見出し、本文、画像、図、表

- 文書の特定のゾーン(=領域)毎にインデックスを作成し文書を検索。
-
ゾーンインデックスにおいて用語が出現するゾーンをpostingsで符号化するメリット
- 辞書のサイズを縮小できる
-
加重ゾーンスコアリングを用いた効率的なスコアリングが可能となる
- クエリに応答して文書をスコアリング(それによってランキングする)
Weighted zone scoring
Learning weights
The optimal weight g
Term frequency and weighting
妥当なスコアリングメカニズムとは
-> クエリに含まれる各クエリ語と文書とのマッチスコアの総和であるスコアを計算
-> クエリ用語の出現回数が多い文書やゾーンは、より高いスコアを獲得する。
-> 高いスコアを獲得した文書やゾーンは、そのクエリとの関連性が高い
クエリ用語の出現回数に応じた重み付け(term frequency)
- 文書
d t -
d t t d - the bag of words model(単語袋モデル)と呼ばれる。
- バッグの中身はは並べられずにゴチャゴチャのイメージ
- クエリ用語の順番を考慮せず、中身が一緒なら同じと考える。
- 順序を無視しても直感的には同じ内容(bag of words)とみなせる。
- 例えば以下の文章は逆の意味だが、同じ内容とみなしても問題なさそう。
- 'Mary is quicker than John'
- 'John is quicker than Mary'
本当にクエリ用語の出現回数のみを重視してよいか?
- No
- stop words(文書を特徴付ける用語ではない用語(例:I, You, Itなど))は無視する必要がある。stop wordsはインデックスに含めたくない。
- 関連性の低いクエリ用語の影響度を軽減するメカニズムが必要。
-> Inverse document frequencyを用いる。
Inverse document frequency
- 多くの文書に出現するクエリ用語は影響度を軽減したい(=重み付けを減らしたい)。
- コレクション全体で頻繁に出現する用語は、用語と文書の関連性の判断に意味を持たない用語だから。

| 記号 | 意味 |
|---|---|
| 逆文書頻度(Inverse document frequency)。クエリ用語(t)の影響度。すなわちあるクエリ用語がどれだけ文書を特徴付けるかを示す値。 | |
| コレクション内の文書の数 | |
| あるクエリ用語(t)が出現する文書の数(document frequency) |
- 稀な用語(=特定の文書にのみ出現する用語=文書と用語の関連性が強い)の場合、
{idf}_{t} - 頻度の高い用語(=多くの文書に出現する用語=文書と用語の関連性が弱い)の場合、
{idf}_{t}
-> クエリ用語が出現する文書数に応じてクエリ用語を重み付けできる。
なぜ{cf}_{t} {df}_{t}

- コレクション(全ての文書の集合)に含まれるクエリ用語の出現回数(=
{cf}_{t} {cf}_{t} - その場合、そのクエリ用語の影響度が小さいクエリ用語である、すなわちそのクエリ用語は文書を特徴付けるクエリ用語ではないと(誤って)判断してしまう。
- しかし、他の文書には出現しないがその文書に出現するのであれば、そのクエリ用語と文書は強い関連性を持つ。
- 「クエリ用語と関連の強い文書を検索する」ことを目的とした場合、「文書を特徴付けるクエリ用語は高く評価」した方が望ましい。
- したがって、「文書全体の出現回数」よりも「出現した文書の数」で評価する方が望ましい。
tf-idf weighting
TF-IDF(Term Frequency-Inverse Document Frequency)は、文書内の各単語の重要度を計算するための手法です。
| 記号 | 意味 |
|---|---|
| tf-idfウェイト。クエリ用語(t)の重み。ある文書(d)における用語(t)の重要性。クエリ用語(t)の出現回数とクエリ用語(t)の影響度の積で算出。 | |
| あるクエリ用語(t)のある特定の文書(d)における出現回数(term frequency in a paticular document) | |
|
|
{idf}_{t}
- クエリ用語(t)が少数の文書内で何度も発生する場合に希少性が最も高くなります(したがって、用語(t)が含まれる文書に識別力を与えられる)。
- クエリ用語(t)が多くの文書で出現する場合は、クエリ用語(t)の希少性は低くなります(したがって、用語(t)が含まれる文書に識別力を与えられない)。
- クエリ用語がすべての文書に出現する場合、最も低くなります(分母の
N log\frac{N}{{df}_{t}}
- クエリ用語がすべての文書に出現する場合、最も低くなります(分母の
スコアリングの計算式
- 文書(
d t d t - クエリにA、B、Cのクエリ用語が含まれている場合、A、B、Cそれぞれの
{tf\_idf}_{t,d}
- クエリにA、B、Cのクエリ用語が含まれている場合、A、B、Cそれぞれの
- 文書(
d t d t tf\_idf
The vector space model for scoring
- 全セクションで整理したように、各文書を重みのベクトルとして見ることによって(=
{tf\_idf}_{t} {tf\_idf}_{t} - ベクトル空間モデルとは、文書の集合(検索クエリや検索対象の文書)を共通のベクトル空間におけるベクトルとして表現すること。
- クエリを文書コレクションと同じベクトル空間におけるベクトルとして捉える
- クエリと文書コレクションを定量的に比較できるようになる
- ベクトル空間モデルは多くの情報検索操作の基本となる
- クエリに対する文書のスコアリング
- 文書の分類(classification)
- 文書のクラスタリング(clustering)
Dot products(ベクトルの内積)
- 文書
d \vec{V}(d) - ベクトルの成分は文書内の用語で構成される。
- ベクトルの各成分の値は
{tf\_idf}_{t}
- コレクション内の文書
d
コサイン類似度(Cosine simirality)
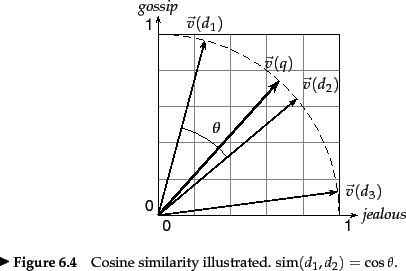
- 文書
d_1 d_2 - ベクトル空間における2つの文書間の類似度を定量化する方法
- コサイン類似度は
\vec{V}(d_1) \vec{V}(d_2)
-
2つのベクトル
\vec{x} \vec{y} \vec{x} \cdot \vec{y} \sum_{i=1}^Mx_iy_i -
文書
d \vec{V}(d) \vec{V}(d) M \vec{V}_1(d)\ldots \vec{V}_M(d) d \sqrt{\sum_{i=1}^M\vec{V}_i^2(d)} -
\vec{V}(d_1) \vec{V}(d_2) \vec{v}(d_1)=\frac{\vec{V}(d_1)}{|\vec{V}(d_1)|} \vec{v}(d_2)=\frac{\vec{V}(d_2)}{|\vec{V}(d_2)|} sim(d_1,d_2)=\vec{v}(d_1)\cdot\vec{v}(d_2)
コサイン類似度をどのように用いるのか?
- ある文書(コレクションに含まれる可能性のある文書)が与えられたとき、その文書に最も似ているコレクション内の文書を検索することを考える。
- このような検索は、ユーザーがある文書(例:検索クエリ)を特定し、その文書に似た他の文書(例:WEB上のあらゆるWebページ)を探すようなシステムで有用である。
- 最も似ている文書
d \vec{v}(d)\cdot \vec{v}(d_i) d_i -
\vec{v}(d) \vec{v}(d_1),\ldots,\vec{v}(d_N) sim(d,d_i)
なぜベクトル間のベクトル差で類似度を測定することはNGなのか?
-
2つの文書ベクトル間のベクトル差を類似度の尺度とする場合
- ベクトルの方向が同じ(=相対的には類似する用語)であっても、ベクトルの長さが異なると、差が大きくなる(=類似していないと判断される)
- よってベクトル間のベクトル差を用いて類似度を定量化することは不適切
->コサイン類似度で類似度を定量化すべし
Queries as vectors
- クエリと各ドキュメントのドット積を計算してスコアを算出
- クエリを「単語の集まり」と見なすことで、非常に短いドキュメントとして扱うことができる。
- 結果として、クエリベクトル
\vec{V}(q) \vec{V}(d) sim(q,d) - 結果のスコアを使用して、クエリに対して最高スコアのドキュメントを選択。
Computing vector scores
前提
- それぞれがベクトルで表されるドキュメントのコレクションがある。
- ベクトルで表されるフリーテキストクエリがある。
- 正の整数
K - 指定されたドキュメントコレクションから、クエリとのベクトル空間スコアが最も高い
K - 通常、これらの上位
K - 多くの検索エンジンは、上位
K=10
- 通常、これらの上位
アルゴリズムの概要
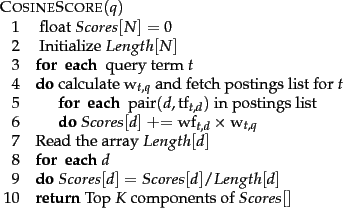
-
Step1:配列Lengthには各
N -
Step3:各クエリ語
t -
Step5:用語
t -
Step6~8:用語
t - このようにクエリ語の寄与を1つずつ加算していく処理は、term-at-time scoringまたはaccumulationと呼ばれることがあり、配列
Scores N - 一度に1つの文書のスコアを計算するdocument-at-a-time scoringもある。
- このようにクエリ語の寄与を1つずつ加算していく処理は、term-at-time scoringまたはaccumulationと呼ばれることがあり、配列
-
Step9:最終的にスコアが計算される
-
Step10:スコアの最も高い
K -
Step12:上位
K - 優先度キューデータ構造が必要で、多くの場合ヒープを使って実装される。
- このようなヒープは
2N O(◆log N) K
-
この目的のために、各投稿エントリに、文書
d t tmbox{wf}_{t,d}
-実際、この重みを保存するには浮動小数点数が必要になる可能性があるため、これは無駄である。このスペースの問題を軽減するのに役立つアイデアが2つある。第一に、逆文書頻度を使う場合、t N/mbox{df}_t mbox{tf}_{t,d}
Variant tf-idf functions
- 各文書内の各用語に重みを割り当てるために、
tf tf-idf - 以下の方法がある(詳細は割愛)
- Sublinear tf scaling
- Maximum tf normalization
- Document and query weighting schemes
- Pivoted normalized document length
Topics
Parametric and Zone indexes
パラメトリックおよびゾーンインデックスは、情報検索の分野で使用されるインデックス構造の一種です。パラメトリックインデックスは、検索対象の文書をパラメーターに基づいてインデックス化する方法です。一方、ゾーンインデックスは、文書内の特定の領域(ゾーン)ごとにインデックスを作成します。これにより、検索クエリが特定の領域に対して限定された場合に、効率的な検索が可能となります。
Weighted Zone Scoring
重み付けゾーンスコアリングは、情報検索において異なる部分(ゾーン)への重み付けを行い、それらを組み合わせて文書のランキングを行う手法です。各ゾーンへの重みは、そのゾーンがクエリにどれだけ関連性があるかを示します。これにより、文書内の異なる部分が異なる重要度を持つ場合に、より適切な検索結果を得ることができます。
Ranked Boolean Retrieval
ランク付けブール検索は、ブール演算子(AND、OR、NOTなど)を使用して検索クエリを行い、結果をランク付けして返す手法です。ブール検索では、クエリにマッチするか否かのみが考慮されますが、ランク付けブール検索では、マッチ度合いに応じて文書をランク付けし、より関連性の高い結果を上位に表示します。
Learning weights
重み学習は、検索モデルやランキング関数における重みパラメータを、訓練データから学習する手法です。機械学習アルゴリズムを用いて、クエリと文書の関連性や他の関連データを元に、各重みの最適な値を自動的に決定します。
The optimal weight g
最適な重みg は、情報検索の分野で用いられるランキング関数において、最適な結果を得るための重みパラメータです。これは通常、機械学習アルゴリズムによって学習され、検索システムのパフォーマンスを最適化するために使用されます。
Term frequency
用語の頻度は、文書内で特定の用語が出現する頻度を示す指標です。情報検索では、用語の頻度が高いほどその用語が重要であると見なされ、検索結果のランキングに影響を与えることがあります。
Tf-idf weighting
Tf-idf(Term frequency-inverse document frequency)重み付けは、情報検索において用いられる用語の重み付け手法の一つです。用語の頻度(tf)と逆文書頻度(idf)の積で計算され、特定の文書における用語の重要度を示します。高いtf-idf値を持つ用語ほど、文書内で重要であると考えられます。
Vector space model for scoring
ベクトル空間モデルは、情報検索における文書やクエリをベクトルとして表現し、ベクトル間の距離や類似度を計算する手法です。スコアリングのためのベクトル空間モデルでは、文書とクエリのベクトル表現を比較し、類似度や関連度をスコアとして算出します。
Cosine similarity
コサイン類似度は、ベクトル空間モデルにおいて用いられる類似度尺度の一つです。2つのベクトル間の角度(余弦)を計算し、その値が1に近いほどベクトルが類似していると見なされます。情報検索では、文書やクエリの類似度を評価するために広く使用されます。
Term-document matrix
用語-文書行列は、情報検索において用いられるデータ構造の一つであり、行が文書、列が用語で構成される行列です。各要素は、文書内の用語の出現回数やtf-idf値などで表され、情報検索のための特
参考文献
Christopher D. Manning, Prabhakar Raghavan and Hinrich Schütze, Introduction to Information Retrieval, Cambridge University Press. 2008.
Discussion