Information Retrieval | 05 Index Compression

Index compression（索引の圧縮）

• 3つのメリットがある。

1. 必要なディスク容量の削減
   • 75%を削減可能
2. キャッシュの利用増→処理スピードUP。より多くの情報をメインメモリに格納可
   • 解凍処理のコストを小さくすることが可能
3. ディスクからメモリへのデータ転送速度の高速化。入出力（I/O）時間を短縮。
   • 非圧縮データの転送時間　＞　データ圧縮時間　＋　圧縮データの転送時間　＋圧縮データの解凍時間
   • データ解凍処理が高速であることが前提

Lossy Compression（非可逆圧縮）

• 一部の情報が破棄される。
  • 手法例１：大文字小文字の折りたたみ、ステミング、ストップワードの除去
  • 手法例２：ベクトル空間モデル(第6章)や潜在的意味インデックス(第18章)のような次元削減技法
  • 使用例：MP3
• 可逆圧縮よりも高い圧縮効率が実現できる。

Statistical properties of terms in information retrieval（情報検索における用語の統計的性質）

• 用語数は辞書のサイズを決定する主な要因。
• 前処理により用語数を圧縮できる（terms、nonpositional postings、positional postingsのそれぞれで圧縮割合は変わる）。
  • No numbers（数字の削除）：2〜9%の圧縮
  • Case foldings（大文字と小文字の同一視）：0〜17%の圧縮
  • 30 stop words（上位30単語の削除）：0〜31%の圧縮
  • 150 stop words（上位150単語の削除）：0〜47%の圧縮
  • Stemming（語幹に揃える）：0〜17%の圧縮
• 非可逆圧縮を使用しても、効果が低下しない検索シナリオが存在
  • 非可逆圧縮において失われた情報が検索システムで使われる可能性が低い場合、非可逆圧縮は理にかなっている。
    • ウェブ検索について、ユーザーは結果の最初の数ページしか見ないという特徴がある。リストの下位にあるドキュメントのpostingを無視できる。
    • MP3において、多くの聞き手は削減された音に気付かない。

Heap's Low(ヒープの法則)

ヒープの法則によると、推定語彙サイズ（M）は、すべての文書から解析された用語の総数（T）、定数k、定数βを用いて以下の通り算定できる。

$$M = kT^ß$$

• M = 推定語彙サイズ
• T = 文書コレクションに含まれるトークンの数
• k = 定数（経験則に基づき、通常は10〜100の範囲）
• β = 定数（経験則に基づき、通常は0.4〜0.6の範囲）

ヒープの法則が示唆すること

1. 辞書のサイズはコレクション内の文書が増えるにつれて増加し続ける
2. 大規模なコレクションでは 辞書のサイズが非常に大きくなる

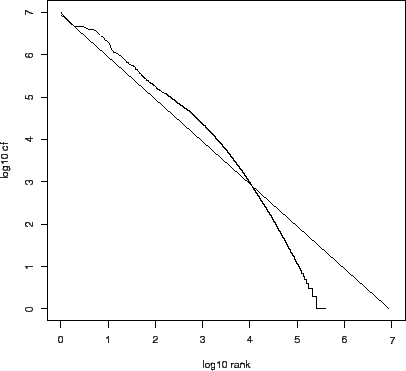
Zipf's law: Modeling the distribution of terms（Zipの法則:項の分布のモデル化）

• コレクション内の用語の分布の一般的なモデルは、Zipfの法則に従う。

• Zipfの法則によると、$t_1$が最も出現頻度の高い単語、$t_2$が２番目に出現頻度の高い単語、......と続くとすると、$i$番目に出現頻度が多い単語の出現頻度を$cf_i$とすると、$cf_i$は$\frac{1}{i}$に比例する。

$$cf_i \propto \frac{1}{i}$$

• つまり、最も頻度の高い単語の出現回数と比較して、2番目に頻度の高い用語の出現回数（$cf_2$）はその1/2、3番目に頻度の高い用語の出現回数（$cf_3$）はその1/3、というようになる。
• 直感的には、順位(rank)が上がるにつれて単語の出現頻度(cf)は急速に減少する。

Dictionary compression（辞書の圧縮）

• Question：なぜ辞書を圧縮する必要があるのか？
  • ディスクへのシーク回数を減らしたい。I/O処理は時間がかかる。
  • 辞書を圧縮すれば辞書をメインメモリ内に収めることができる。
    →ディスクへのシーク回数が減る。
  • 非圧縮の辞書がメモリに収まらない例
    • 大企業の検索サーバー。多くの異なる言語が存在するため容量が大きい。
    • 携帯電話や車載コンピュータ。メモリの容量が小さい。。
    • PC上の検索システム。複数のアプリケーション間でメモリを共有する必要性。

Dictionary as a string

Dictionary-as-a-string storage

• 辞書の最も単純なデータ構造
• 語彙を辞書順にソートし、固定幅エントリの配列に格納
  • Unicode表現を想定すると、用語自体に2 $\times$ 20バイト（英語では20文字以上の用語はほとんどないため）、文書頻度に4バイト、投稿リストへのポインタに4バイトを割り当てる
• 用語に固定幅を使うのは無駄。
  • 英単語の平均的な長さは約8文字なので、固定幅のスキームでは平均して12文字（または24バイト）を無駄にする。
• 固定幅に収まらない用語を格納できない。

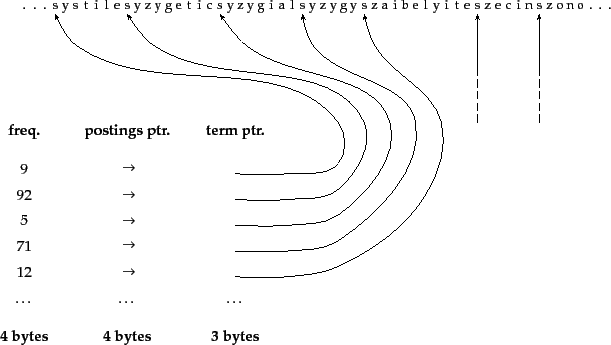
• ポインタ(term ptr)は、前の項の終わりと次の項の始まりを示します。例えば、この例の最初の3つの用語は、systile、syzygetic、syzygialである。

Blocked storage with four terms per block

• 辞書の用語を1つの長い文字列として格納
• 各項の前には、その長さをエンコードするバイトが置かれる。つまり、次の項に到達するために何バイトスキップすべきかを示す。
• 次の項へのポインタは、現在の項の終わりを示す用途もある。
• 上記のデータ構造の欠点を克服できる。固定幅のストレージに比べて60％の節約。

• 最初のブロックはsystile、syzygetic、syzygial、syzygyで構成され、長さはそれぞれ7文字、9文字、8文字、6文字である。各項の前には、その長さをエンコードするバイトが置かれ、後続の項に到達するために何バイトスキップすべきかを示す。

Blocked storage

• Blockingにより辞書を圧縮する仕組み
  • 文字列内の項をサイズkごとにグループ化
  • 各ブロックの先頭項のみに項ポインタを保持
  • 文字列中の項の長さは、項の先頭に追加バイトとして格納
• k-1個の項ポインタは不要になるが、各項の長さを格納するためにkバイトの追加バイトが必要

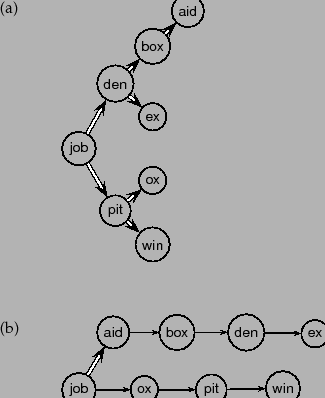
Blocked storageの具体例（k=4の場合）

• ドキュメント全体（圧縮前）：400,000bytes

• １ブロックあたりのterm数：k=4 term

• ドキュメントに含まれるブロック数：400,000bytes÷ 4term = 100,000ブロック

  • 4termsが1セットとなって1つのブロックに含まれる。

• １ブロックあたりのtermポインタの削減：(k-1)×3bytes=9bytes

  • 各ブロック毎に最初のterm以外のk-1個のterm（すなわち4-1=3つのterm）はtermポインタ（このケースでは3bytesと想定）は不要となる

• １ブロックあたりのterm lenghtの追加：k=4bytes

  • 1ブロック内のk個のtermそれぞれについて、termの文字数を格納する領域が必要になる。
  • 文字列を格納するよりもコンパクトなメモリ使用量で済む。

• 1ブロック（k文字単位）あたりの削減量：9bytes - 4bytes　= 5bytes

• ドキュメント全体での削減量：100,000ブロック × 5bytes = 500,000bytes
  
  出典：CS3308 Information Retrieval Unit 3 Lecture 2, From fabian.glagovsky, https://my.uopeople.edu/mod/kalvidres/view.php?id=403044

Front Coding

• アルファベット順に並べられたリストの連続する項目が共通の接頭辞を持つという事実である。
• 前方符号化により、共通する接頭辞は、用語リストの部分列で識別され、特別な文字で参照される。

Minimal Perfect Hashing

• さらに圧縮率の高い他のスキーム
• M個の用語を衝突なしに$[1,˶,M]$にマップするハッシュ関数に依存
• しかし、完全ハッシュは新しい項が増えるたびに衝突を起こし、新しい完全ハッシュ関数を作る必要があるため、段階的に適応させることはできない。
• したがって、動的な環境では使用できない。

辞書全体をメインメモリに格納できない場合の対応

• 非常に大規模なテキスト・コレクションや、限られたメモリしか持たないハードウェアの場合
• 辞書をディスクに格納されるページに分割
  • Bツリーを使用して、各ページの最初の項にインデックスを付ける。
  • ほとんどのクエリを処理するために、検索システムは投稿をフェッチするためにディスクに移動
  • ディスクから用語の辞書ページを取得するためにシークが1回追加されることはクエリ処理にかかる時間を大幅に増加させるが（I/O処理のため）、許容範囲内。

Postings file compression

• 投稿と投稿の間のギャップが短く、20ビットよりもはるかに少ないスペースで格納できることである。
  • theやforのような最も頻度の高い用語のギャップは、ほとんどが1ビットに等しい。
  • コレクションの中で1度か2度しか出現しない稀な用語は20ビットを必要とする。
• 短いギャップに対してより少ないビットを使用する可変エンコード方法が必要
• 小さな数を大きな数よりも少ないスペースで符号化するための方法
  • バイト単位の圧縮 -> 最小のバイト数でギャップをエンコード
  • ビット単位の圧縮 -> 最小のビット数でギャップをエンコード

Variable byte codes

• 可変バイト(VB)エンコーディングは、ギャップをエンコードするために整数バイトを使う。

• バイトの最後の7ビットはペイロードであり、ギャップの一部をエンコードする。

• バイトの最初のビットは継続ビット

  • エンコードされたギャップの最後のバイトには1がセットされる。
  • それ以外には0がセットされる。

• 可変バイトコードをデコードするには、継続ビット0を持つバイト列を、継続ビット1を持つバイトで終端して読み込む。

• 次に、7ビット部分を抽出して連結する。

• VB圧縮では、非圧縮インデックスの50%以上の削減。

• VBエンコーディングの考え方は、バイトよりも大きな単位や小さな単位にも適用できる

• ワードを大きくすると、圧縮の効果が落ちる（あるいは圧縮されない）代償として、必要なビット操作の量はさらに減ります。

• バイトより小さいワードサイズは、ビット操作が増える代わりに、圧縮率がさらに向上する。

• 一般的に、バイトは圧縮率と解凍速度の良い妥協点を提供します。

• ほとんどのIRシステムにおいて、可変バイト符号は時間とスペースのトレードオフに優れている。

• 実装も簡単である。セクション5.4で言及されている代替案のほとんどは、より複雑である。

• しかし、ディスクスペースが乏しい場合には、ビットレベルの符号化、特に密接に関連する2つの符号化を使用することで、より優れた圧縮率を達成することができる。

Gamma codes

まとめ途中。後日更新予定。

• Variable byte コードは、ギャップの大きさに応じて適応的なバイト数を使用する。
• ビットレベル・コードは、より細かいビットレベルでコードの長さを適応させる。

unary code

• 最も単純なビットレベル・コード。
• 1の後に0が続く文字列。
• 効率的なコードではないがお手軽。

Milestones

• Explain the need and value of compression within Information Retrieval (IR) systems.
• Describe the different forms of data compression including the difference between lossless and lossy compression.
• Recognize Heaps’ law and be able to calculate the value of M for a collection.
• Recognize Zipf’s law as it relates to the distribution of terms within a collection.
• Implement techniques for dictionary compression.
• Implement techniques for postings file compression.

Topics

• Index compression
• Rule of 30
• Lossless Compression
• Zipf’s law
• Dictionary compression
• Postings file compression
• Variable byte codes (γ codes and δ codes)
• Power law
• Front Coding
• Variable Byte Encoding
• Nibble
• Unary Code
• γ Encoding
• Entropy
• δ Codes