LPFと勾配降下法に関する発見

この記事は，株式会社ACCESS Advent Calendar 2023 の 5 日目の記事です．

前の記事：2023年に生成AIの動向を追いかけて落ち着いた動画情報源（Yam3939）
次の記事：Android11以上で別パッケージにbindServiceしても接続できない場合の改善策（monjyayaki）

概要

ノイズのある時系列データからノイズのない真の値を推測しようとするとき，ローパスフィルタ（LPF） はその選択肢の一つです．
センサなどで発生するノイズは高周波成分とみなせるため，LPF を用いることで取り除くことができます．

真の値を推測する別の方法としては，誤差関数を定義して，その誤差を最小化するようにパラメータを更新する方法が挙げられます．
この方法は，機械学習における最適化アルゴリズムとして知られている確率的勾配降下法（SGD） の基本的な考え方です．

この記事では，LPF と SGD の関係について考察し，LPF が SGD の特殊な場合として得られることを確認します．
また，SGD の改良アルゴリズムについても同様に LPF として解釈できるかを検証します．

背景：ローパスフィルタ（LPF）

ローパスフィルタ（Low Pass Filter; LPF）とは，時間によって変化する入力信号から，高周波成分を減衰させるフィルタのことです．
具体的な実装として移動平均法やガウシアンフィルタなどもありますが，ここでは一次遅れ系について詳しく見ていきます．

一次遅れ系とは，伝達関数 $G(s)$ が以下のようになるフィルタのことです：

$$G(s) = \frac{K}{1 + \tau s}$$

ここで，$K$ は定常ゲイン，$\tau$ は時定数と呼ばれる定数です．
入力の位相が遅れて出力される系の中で，伝達関数が $s$ の一次式で表されることから，このフィルタは一次遅れ系と呼ばれています．

フィルタの特性を表す指標として，遮断周波数があります．
遮断周波数とは，フィルタ回路において入力信号のゲインが $\frac{1}{\sqrt{2}}$ 倍になる境界の周波数のことです．
Bode 線図では，遮断周波数はゲインが $\approx -3\ \mathrm{dB}$ になる周波数として表されます^[1]．
一次遅れ系の遮断周波数 $f_c$ は，以下の式で求めることができます：

$$f_c = \frac{1}{2 \pi \tau}$$

背景：確率的勾配降下法（SGD）

ある関数 $f(y)$ について，特定の条件下で $f(y)$ が最小（あるいは最大）となる $y$ を求める問題を最適化問題といいます^[2]．
勾配降下法は，そのような最適化問題を解くためのアルゴリズムの一つです．
具体的には，まず初期値 $y_0$ を解に近い値として設定し，以下の更新式によって $y_n$ を更新していきます^[3]：

$$y_{n + 1} = y_n - \eta f'(y_n)$$

$\eta > 0$ は学習率と呼ばれる定数で，この値が大きいほど更新の幅が大きくなりますが，収束までの過程が不安定になることがあります．
このように更新することで，$n$ が大きくなるにつれて $f(y_n)$ が極小値に近づいていきます．

機械学習では，$f(y)$ を入力データとの誤差を表す損失関数として定義し，その損失を最小化するようにパラメータを更新することで入力との誤差を徐々に小さくしていき，学習を進めます．
確率的勾配降下法（Stochastic Gradient Descent; SGD）とは，入力データを 1 つずつ取り出してその都度勾配降下法を適用し，パラメータを更新するアルゴリズムです．
入力データをいちどに全て取り出して更新を適用するバッチ勾配降下法と比べて，SGD は計算コストが低く，局所解に陥りにくいという特徴があります．

発見：LPF と SGD の関係

ここで，入力との二乗誤差を損失関数としたときの SGD について考えます．
入力データを $x$，出力データを $y$ として，損失関数を以下のように定義します：

$$f(y) = \kappa (y - x)^2 \quad (\kappa > 0)$$

$x$ を固定化したとき，微分 $f'(y)$ は以下のようになります：

$$f'(y) = 2 \kappa (y - x)$$

時間変化する入力 $x_n$ をランダムに取り出されたデータとみなし SGD の式に当てはめると，$y_n$ は以下のように更新されます：

$$y_{n + 1} = y_n - 2 \eta \kappa (y_n - x_n)$$

さて，ここで $x$ を入力，$y$ を出力とした系を考え，伝達関数 $G(s)$ を求めてみます．
値の変化にかかる時間と対応した微小時間 $\Delta t$ による時間差分を導入することで，両辺を離散的に Laplace 変換できます：

$$\frac{\Delta y}{\Delta t} = - \frac{2 \eta \kappa}{\Delta t} (y - x)$$

$\beta = \frac{2 \eta \kappa}{\Delta t}$ とおき^[4]，$X(s),\ Y(s)$ をそれぞれ $x,\ y$ のラプラス変換とします．

$$\begin{aligned} sY(s) &= - \beta (Y(s) - X(s)) \\ G(s) = \frac{Y(s)}{X(s)} &= \frac{1}{1 + \beta^{-1} s} \end{aligned}$$

なんと，伝達関数は $\beta / 2\pi$ を遮断周波数とする一次遅れ系 LPF の式と一致しました！

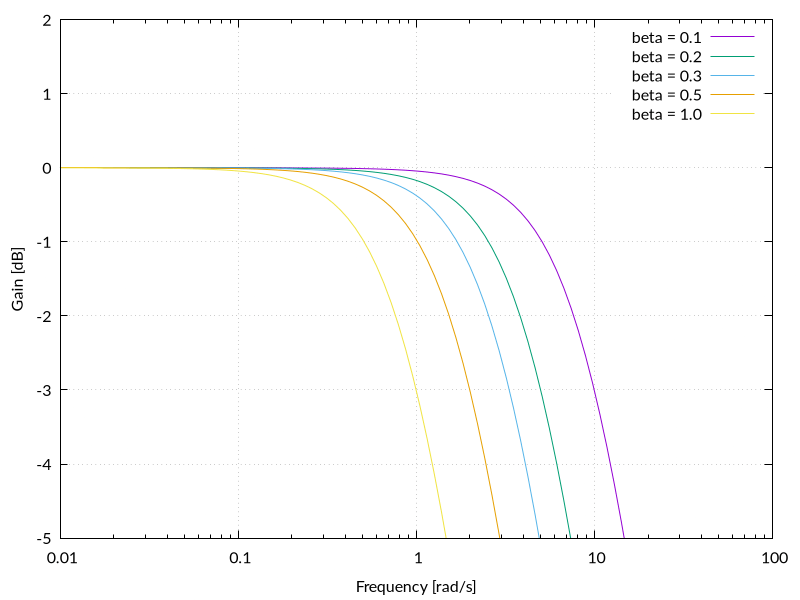
更なる実験

SGD には，様々な改良アルゴリズムが提案されています．
代表的なものとしては以下のようなものがあります：

• Momentum SGD
• Nestelov's Accelerated Gradient (NAG)
• AdaGrad
• RMSProp
• AdaDelta
• Adam

これらのアルゴリズムは，機械学習において，SGD よりも高速に学習できることが知られています．
ここでは，Momentum SGD について，同様に LPF として解釈できるかを検証します．

Momentum SGD

Momentum SGD は，SGD にいわゆる慣性項を加えたアルゴリズムです．
過去の勾配の情報を取り入れることで，高速に学習できることが知られています．

更新式は以下の通りです（$0 \le \alpha < 1$）：

$$\begin{cases} y_{n + 1} = y_n + v_{n + 1} \\ v_{n + 1} = \alpha v_n - \eta f'(y_n) \end{cases}$$

同様に，$f(y) = \kappa (y - x)^2,\ f'(y) = 2 \kappa (y - x)$ として，伝達関数 $G(s)$ を求めてみます．
まず，第 2 式から $v$ の Laplace 変換 $V(s)$ を $X(s),\ Y(s)$ を用いた式に変形します：

$$\begin{aligned} v_{n + 1} - v_n + (1 - \alpha) v_n &= - 2 \eta \kappa (y_n - x_n) \\ sV(s) + \frac{1 - \alpha}{\Delta t} V(s) &= - \frac{2 \eta \kappa}{\Delta t} (Y(s) - X(s)) \end{aligned}$$

ここで $\beta = \frac{2 \eta \kappa}{\Delta t},\ \mu = \frac{\alpha}{\Delta t},\ \nu = \frac{1 - \alpha}{\Delta t}$ とおきます^[4:1][5]．

$$V(s) = - \frac{\beta}{\nu + s} (Y(s) - X(s))$$

続いて両式より $v_{i + 1}$ を消去することで，伝達関数 $G(s)$ を求めることができます：

$$\begin{aligned} y_{n + 1} &= y_n + \alpha v_n - 2 \eta \kappa (y_n - x_n) \\ y_{n + 1} - y_n + 2 \eta \kappa y_n &= \alpha v_n + 2 \eta \kappa x_n \\ sY(s) + \beta Y(s) &= \mu V(s) + \beta X(s) \\ &= - \frac{\beta \mu}{\nu + s} (Y(s) - X(s)) + \beta X(s) \\ &= \frac{\beta (\mu + \nu + s)}{\nu + s} X(s) - \frac{\beta \mu}{\nu + s} Y(s) \\ G(s) &= \frac{\beta (\mu + \nu + s)}{\beta(\mu + \nu) + (\beta + \nu) s + s^2} \end{aligned}$$

Momentum SGD の伝達関数は，二次遅れ系の LPF のものと一致することがわかりました！
$\beta = 0.1$ として $(\mu, \nu)$ を変化させたときの Bode 線図を以下に示します：

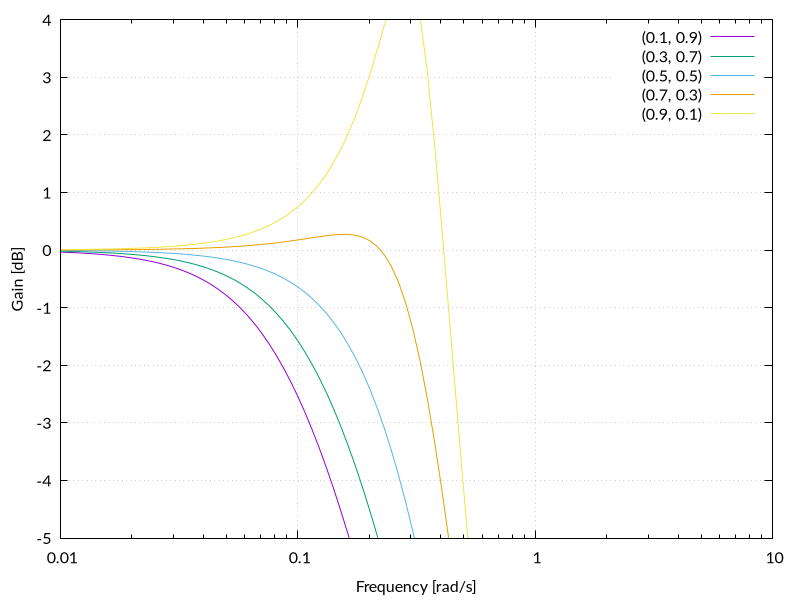
まとめ

目的関数を $f(y) = \kappa (y - x)^2 \quad (\kappa > 0)$ としたとき，SGD によって $y$ を更新することで，$y$ が $x$ の LPF として振る舞うことを確認しました．
また，Momentum SGD についても同様に LPF として解釈できることを確認しました．
他の最適化アルゴリズムの場合はどうなるか気になるところですが，それは今後の課題とします．

脚注

1. $20 \log_{10} \frac{1}{\sqrt{2}} \approx -3.01\ \mathrm{dB}$ であり，$-3\ \mathrm{dB}$ は精度の高い近似値ではあるが，厳密な値ではない．

2. 未知数はふつう $x$ で表されるが，この記事では $x$ を入力データ，$y$ を出力データとしたいため，混乱を避けるために $y$ で統一している．

3. 今回はパラメータが 1 次元の場合を考えるが，一般にパラメータが多次元の場合は $\boldsymbol{\theta}_{n + 1} = \boldsymbol{\theta}_n - \eta \nabla f(\boldsymbol{\theta}_n)$ と更新する．

4. $\beta$ を定数として扱うためには，$\eta$ が $\Delta t$ に比例する必要がある．$\Delta t$ が一定で $\eta$ が変化しない場合は自然にこの条件を満たす．

5. $\beta$ の例と同様に，$\alpha$ が $\Delta t$ に比例している必要がある．