🔖

ヒープソートについて理解する

2023/05/24に公開

アルゴ式のヒープソートの問題を解きました。わからないところをメモしていきます。

#include <iostream>
#include <vector>
using namespace std;

// 配列の中身を表示する関数
void output(vector<int> A) {
    for (int i=0; i<A.size(); ++i) {
        cout << A[i];
        if (i!=A.size()-1) cout << " ";
        else cout << endl;
    }
}

// 二分ヒープの構築
void build_heap(vector<int> &v) {
    for (int x=v.size()/2-1; x>=0; --x) {
        int k = x;
        while (true) {
            // ノードが存在しない場合は 0 を仮置きする
            int left = 2*k+1<v.size() ? v[2*k+1] : 0;
            int right = 2*k+2<v.size() ? v[2*k+2] : 0;

            if (!left && !right) break; // 子ノードが存在しない
            else if (v[k]>=left && v[k]>=right) break; // 最大値が v[k]
            else if (left>=right) { // 最大値が v[2*k+1]
                swap(v[k], v[2*k+1]);
                k = 2*k+1;
            }
            else { // 最大値が v[2*k+2]
                swap(v[k], v[2*k+2]);
                k = 2*k+2;
            }
        }
    }
}

int main() {
    // 入力
    int N;
    cin >> N;
    vector<int> A(N);
    for (int i=0; i<N; i++) cin >> A[i];

    // 二分ヒープの構築
    build_heap(A);

    // 配列の中身を出力する
    output(A);
}

for (int x=v.size()/2-1; x>=0; --x) { }

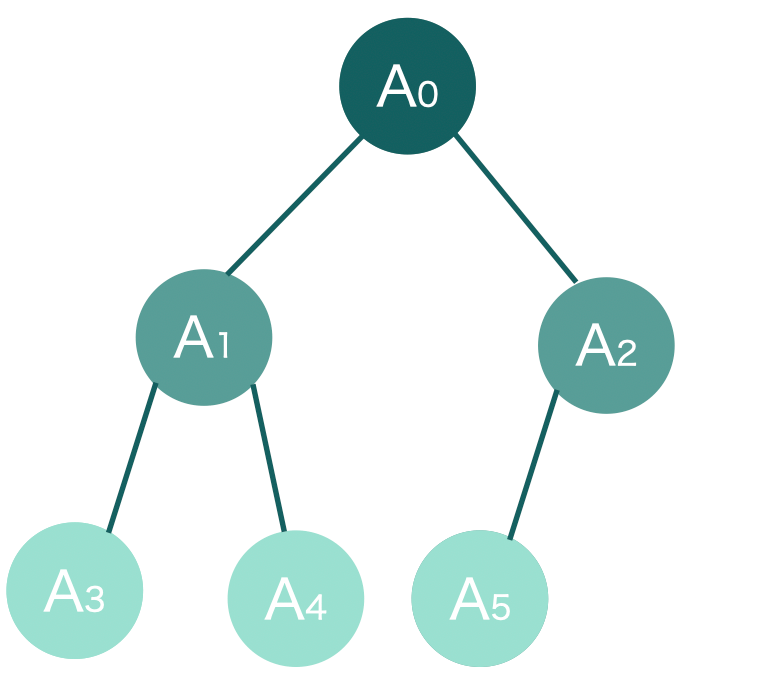
ここでループの初期値はv.size()/2 - 1です。これは最下層の親ノードを表しています。図でいうところのA2です。最下層の親ノードから順に左へ上へと移動していき最終的に親ノードまで遡っています。

整理しておきます

項目	配列上のインデックス
ルート	0
最下層の親ノード	i/2-1
i番目の左の子ノード	2*i+1
i番目の右の子ノード	2*i+2

int left = 2*k+1<v.size() ? v[2*k+1] : 0;
int right = 2*k+2<v.size() ? v[2*k+2] : 0

三項演算子を使って左の子ノードと右の子ノードに数字を代入する操作をしています。二分木は自分のインデックスをkとすると、左の子のインデックスが2*k+1で、右の子のインデックスが2*k+2と表されます。なので条件部分を無視して単に代入するコードをかくと次のようになります。

int left = v[2*k+1];
int right = v[2*k+2];

しかし、子要素は常に存在するとは限りません。

この図でもA2の左の子は存在しますが、右の子は存在しません。配列の存在しないインデックスにアクセスするとエラーが出てしまうので三項演算子で子要素が存在することを確かめてから代入する必要がありそうです。「左の子が存在する」というのをコードに起こすと2*k+1<v.size()となります。
配列にはN個の数字がぎっちり詰め込まれているので、アクセスしようとするインデックスが配列のサイズを超えることはありません。

A1の左の子にアクセスする場合を考えると、A1のインデックスは1なので左の子のインデックスは2*1+1=3です。配列のサイズv.size()は6で、2*k+1<v.size()がtrueとなり、左の子が存在することがわかります。
A1の右の子にアクセスする場合を考えます。A1のインデックスは1なので左の子のインデックスは2*1+2=4です。配列のサイズv.size()は6で、2*k+1<v.size()がtrueとなり、右の子が存在することがわかります。
A2の左の子にアクセスする場合を考えます。A2のインデックスは2なので左の子のインデックスは2*2+1=5です。配列のサイズv.size()は6で、2*k+1<v.size()がtrueとなり、右の子が存在することがわかります。
A2の右の子にアクセスする場合を考えます。A2のインデックスは2なので右の子のインデックスは2*2+2=6です。配列のサイズv.size()は6で、2*k+1<v.size()がfalseとなり、右の子が存在しないことがわかります。

次に条件分岐を見てみます。if文内のコードを省略して抜き出すと４つのパターンに別れていることがわかります。

if (!left && !right)
else if (v[k]>=left && v[k]>=right)
else if (left>=right)
else

通常動作と例外動作にわけて考えます。
ヒープソートの通常の動作は左の子と右の子の大きい方と交換するというものでした。なので左の子と交換する場合は3行目の場合わけで、右の子と入れ替える場合は４行目の場合わけで行います。
例外動作は子要素が存在しない場合とすでにヒープ木の条件を満たしてる場合です。子要素が存在しない場合は1行目の動作で、ヒープ木の条件を満たしている場合は2行目で処理しています。
アーリーリターンの考え方で、例外動作の方を先に持ってきています。

次に各条件について詳しくみていきます。

if (!left && !right)

これは左の子と右の子が存在しない場合を表しています。leftとrightは先ほど紹介したものです。子要素が存在する場合値を代入し、存在しない場合は０を代入しています。 (!left && !right)はleftとrightが共にfalse、すなわち共に0の場合trueになります。c++では0はfalseと処理され、0でなければtrueと認識されます。
ここは例外動作なのでループを抜け出すために breakします。

else if (v[k]>=left && v[k]>=right) について

これはヒープ木の条件を満たしている場合を表しています。ヒープ木の条件は親の値は子の値以上であることなので、現在の値v[k]が左右の子より大きいことをコードに表しています。
ここも例外動作でループを抜け出すために breakします。

else if (left>=right)

ここは通常動作です。親の要素を子の要素を入れ替えるとき、左右の大きい方と入れ替えることにしています。ヒープ木は親子の値の大小関係が要求されているだけで、同じ階層での大小関係は要請されていません。図でいえば、A1とA2の大小関係はどちらでもいいし、A3とA4の大小関係はどちらでも構いません。しかしどっちでもいいというのではコードに落とせないので、左右の子の大きい方と入れ替えることにしています。なので、左の子が大きい場合、このブロックのコードが実行されます。
swapした後kの値を左の値に更新して再びループします

else

ここも通常動作です。ここではelseでまとめられていますが、right>=leftの場合を表しています。アーリーリターンにより例外動作はすでにはじいていて、left>=rightの場合も書いてあるので、elseでまとめています。
swapした後kの値を右の値に更新して再びループします