誰でもわかる線形計画法の理論と実装
はじめまして、まつのです!
機械学習や生成AIの受託開発・AI学習サービス「aipass」の運営をしている株式会社dotConfという会社で、代表をしております!

この記事では、線形計画法の理論をシンプルに解説し、Pythonを用いた実装例を紹介します。
線形計画法とは?
「限られた資源の中で、できるだけ得をしたい」 これが線形計画法の本質です。
もう少し数学的な表現をすると、与えられた制約条件のもとで、目的関数(コストや利益など)を最大化または最小化する問題を解くことための方法です。
例えば…
- レストランが「限られた食材」で「利益を最大化」したい
- 工場が「限られた時間と材料」で「生産量を最大化」したい
- 学生が「限られた時間」で「効率よく勉強」したい
こうした問題は「線形計画法」で表現できます。
お菓子工場の利益最大化
この記事ではお菓子工場の利益の最大化をテーマに解説します。このお菓子工場では 「チョコレート」 と 「クッキー」を作っています。それぞれの製品は「材料」と「時間」を使い、そして「利益」を生みます。
| 製品 | 材料(kg) | 時間(h) | 利益(円) |
|---|---|---|---|
| チョコレート | 2 | 1 | 300 |
| クッキー | 1 | 2 | 200 |
工場の制約は次の通りとします:
- 材料は 最大22kg
- 作業時間は 最大20h
工場の制約を満たしながら利益を最大化するためにはチョコレートとクッキーをいくつずつ作成すればよいかを考える必要があります。チョコレートの個数を
- 目的関数(利益の合計を最大化)
- 制約条件
となります。
Pythonでの実装
Pythonの scipy.optimize.linprog を使うと、すぐに解けます。
from scipy.optimize import linprog
# maximize 300x1 + 200x2
# linprogはminimize形式なので符号を反転
c = [-300, -200]
# 制約条件
A = [[2, 1], # 材料
[1, 2]] # 時間
b = [22, 20]
# x1, x2 >= 0
res = linprog(c, A_ub=A, b_ub=b, bounds=(0, None))
print("最適解 (x1, x2):", res.x)
print("最大利益:", -res.fun)
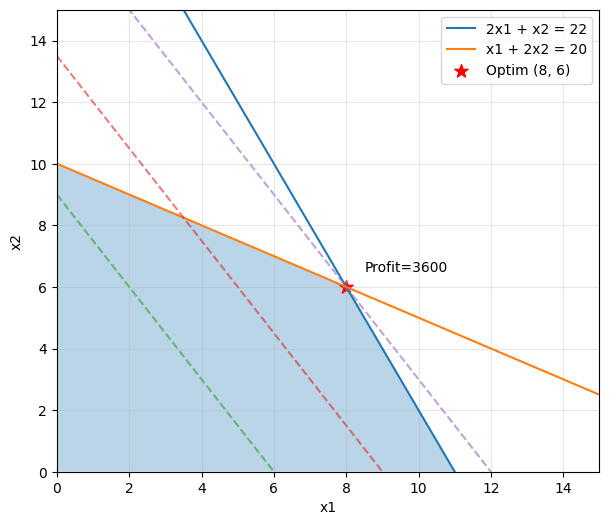
実行結果はこちら👇
最適解 (x1, x2): [8. 6.]
最大利益: 3600.0
つまり、
• チョコレートを8個
• クッキーを6個
作ると、 利益3,600円 が最大になります!
「制約条件を守りながら、できるだけ儲かる組み合わせを探す」これが線形計画法です。最適解は 制約条件で囲まれた多角形の「頂点」 に現れることが理論的に保証されています。今回も「チョコ8個・クッキー6個」という頂点の組み合わせが最適解でした。
その他の数理最適化手法
数理最適化の手法は線形計画法以外にも多くの種類が研究されてます
| 手法 | 特徴 |
|---|---|
| 線形計画法 | 目的関数と制約が「線形」。高速に解ける。 |
| 整数計画法 | 変数を整数に制限。組合せ最適化(例:配送ルート問題)で利用。 |
| 混合整数計画法 | 線形計画法と整数計画法の組み合わせ。より実務的な制約を表現可能。 |
| 非線形計画法 | 目的関数や制約が非線形。計算は難しいが表現力が高い。 |
| 動的計画法 | 問題を分割して解く手法。最短経路やスケジューリングで活躍。 |
| メタヒューリスティクス | 厳密解は保証せず、良い近似解を見つける。遺伝的アルゴリズムやシミュレーテッドアニーリングなど。 |
データサイエンティストを目指す人へ
Pythonを活用してAI学習を目指す方へ👇
Pythonを体系的に学び、プロの指導のもとで実践的なAIスキルを習得したい方、
キャリアの幅を広げたい方や複業を目指す方は、ぜひこちらからお問い合わせください。
Discussion