AlphaQuoridor（アルファ・コリドール）の理論と実装

日本ではあまり馴染みのないボードゲームであるQuoridor（コリドール）を題材に、深層強化学習のAlphaZeroを適用しました。AlphaZero自体はシンプルな設計であるにも関わらず、囲碁・将棋などでプロ棋士を圧倒する威力を発揮する強力な強化学習の手法です。この記事をきっかけに、AlphaZeroの理論的理解と、実装に関する技術的理解を深めて頂けたら嬉しいです。

Quoridor（コリドール）とは？

wikipediaによると、Quoridor（コリドール）について下記のように説明されています。

Quoridorは、コマの移動と壁の設置によって先にゴールに到達することを目指す、フランスのボードゲーム（アブストラクトゲーム）である。

https://ja.wikipedia.org/wiki/コリドール

具体的なルールは下記の通りです。

セットアップ：

2人用では、各プレイヤーはボードの中央列の自分側端に駒を置く。各プレイヤーに10枚の壁（ブロック）を配る。

4人用では、各プレイヤーはボードの中央列の自分のコーナーに駒を置き、各プレイヤーに5枚の壁を配る。

プレイの進行：

• プレイヤーは交互に手番を行い、以下のいずれかを選択できる：
  • 駒を上下左右のいずれかの隣接するマスに1マス進める。
  • 壁をボード上に配置する（壁は2マスを横切る形で置くことができる）。
• 駒は他の駒を飛び越えることができるが、壁を飛び越えることはできない。もしも、他の駒を飛び越える先に壁がある場合は、その駒の左右に移動できる（もし左右も壁である場合はその駒の方向へは移動できない）。
• 壁は完全にプレイヤーの駒の進路をふさぐように配置してはならない。

勝利条件：

• いずれかのプレイヤーが自分の駒を自分の初期位置とは反対側の一列に到達させた時点でそのプレイヤーの勝ちとなる。

シンプルなルール設計でありますが、「壁は完全にプレイヤーの駒の進路をふさぐように配置してはならない」というルールがあることによって、最終盤までどちらが勝つかがわからないというドキドキ感が楽しめるゲームです。

AlphaZeroの理論

AlphaZero [1, 2] は大きく分けて、深層学習・探索・強化学習の３つの要素が構成されています。それぞれどのようなことに使われているか見ていきましょう。

深層学習

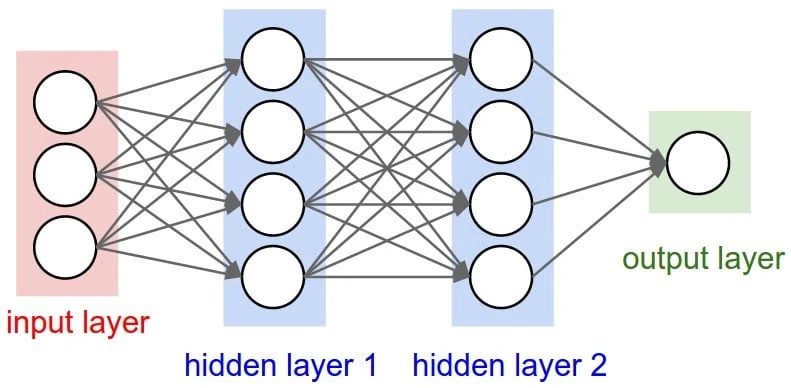
深層学習は、AlphaZeroの「直感力」に当たる部分の役割を担っています。将棋のプロ棋士がよく「この場合はこの手が筋」と話されていることをよく耳にすると思いますが、まさにこのような各場面に対して何が最善手であるかを考える脳であると言えます。

AlphaZeroの深層学習では、畳み込みニューラルネットワークの一種で画像分析において一定の成果を出しているResNet [3] と呼ばれるものを使用しています。今回はニューラルネットワークの入力としてゲームの盤面を入れるわけですが、ゲームの盤面も画像と同じく２次元上に並ぶ情報の集合に過ぎないため、画像処理と同様に一定の成果が見込めると期待できるのです。数式でまとめると次のように表せます。

$$\mathrm{ResNet}(s) = \pi(a | s), v(s)$$

ここで、${s}$はゲームの盤面（状態）、${\pi(a | s)}$は方策（状態${s}$のときに行動${a}$をとる条件付き確率）、${v(s)}$は状態${s}$での価値（勝ち+1、負け-1）です。

探索

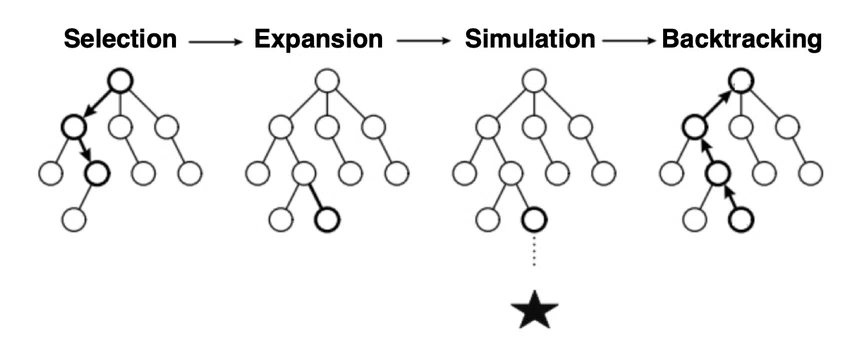
将棋・囲碁・オセロ・今回のコリドールなどは二人ゼロ和有限確定完全情報ゲームに分類され、最善の戦略方法はミニマックス法（あるいはより計算効率の良いアルファベータ法）で求められます。しかし、これらは（ほとんど）全ての手を調べ尽くす必要があり、合法手が多いゲームでは現実的には探索不可能です。そのため、ゲーム探索においては、現実的な時間で実行可能なアルゴリズムであるモンテカルロ木探索がよく使用され、AlphaZeroでもこの「先読み力」を用いて将来の手を予測しています。

AlphaZeroのモンテカルロ木探索では下記のUCBと呼ばれる評価値を基に、次にどの手を取るかを決定します。

$$\mathrm{UCB}(s, a) = Q(s,a)+ c \cdot \pi(a | s) \cdot \frac{\sqrt{N(s)}}{1+N(s, a)}\\Q(s, a) = \frac{1}{N(s, a)} \displaystyle \sum_i^{N(s, a)} v_i(s\stackrel{a}{\to} s^\prime)$$

ここで、${Q(s, a)}$は状態${s}$における行動${a}$の価値推定値であり、状態遷移後の状態${s^\prime}$における累計価値を、状態${s}$から行動${a}$へのシュミレーション回数${N(s, a)}$で平均値です。また、${N(s)}$は状態${s}$における総シミュレーション回数です。第１項目は価値の高いものを利用することを意味しており、第２項目はまだシュミレーションされていない行動について探索することを意味していて、それら利用と探索の配分についてはハイパーパラメータである${c}$で調節されます。

シュミレーションを繰り返すことで、シュミレーション回数${N(s, a)}$が多い行動${a}$が価値が高い手となります。

実際には、状態${s}$においてどの行動${a}$を取るかというのは、下記のように温度${T}$のボルツマンで重み付けされた確率で${\pi(a | s)}$によって決められます。

$$\pi(a | s) = \frac{\displaystyle N(s, a)^{1/T}}{\displaystyle \sum_b N(s, b)^{1/T}}$$

強化学習

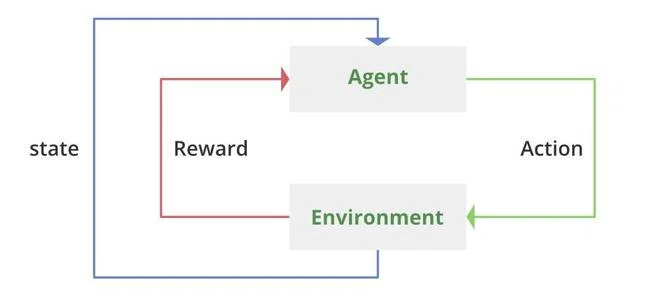
AlphaZeroはResNetを用いたモンテカルロ探索によって自己対戦し、さまざまな盤面状態とそれに対する最適な手のデータ（方策と価値）を生成します。この「経験」データをResNetに使うことで、より賢いニューラルネットワークが作成できます。

強化学習の一連の流れは下記のようになります。

1. ResNetのパラメータの初期化
2. 自己対戦による「経験」データの取得
3. 取得データを使用したResNetのパラメータの更新
4. 2, 3を一定回数繰り返す

AlphaQuoridorの実装

AlphaQuoridorの実装の流れは下記のようになります。全てのコードは下記のGitHub上にアップロードしてあります。

https://github.com/dorakingx/AlphaQuoridor

• ゲーム設計（game.py）
• 深層学習：ResNetの実装（dual_network.py）
• 探索：モンテカルロ木探索の実装（pv_mcts.py）
• 強化学習：ゲームをプレイして経験データを取得（self_play.py）
• 経験データからResNetのパラメータを更新（train_network.py）
• ベストパラメータとの最新のパラメータを比較し更新（evaluate_network.py）
• ベストプレイヤーを実際に対戦させて評価する（evaluate_best_player.py）
• 今までの学習サイクルを一括で実行する（train_cycle.py）
• 完成したAIと対戦できるゲームUIの実装（human_play.py）

実装に関しては下記の本を参考にして作成していますので、より詳しい説明が知りたい方は手に取ってみると良いと思います。

https://www.amazon.co.jp//AlphaZero-深層学習・強化学習・探索-人工知能プログラミング実践入門-布留川-英一/dp/4862464505

今回は、学習時間をできる限り短くするために、ゲームサイズを３x３で強化学習させています。なので、ゲーム性という観点からあまり面白いものではないですが、ゲームサイズはすぐに変えられるように実装してますので、学習時間が長くなっても良いのであれば、５x５でも、また実際のサイズである９x９で試してみるとより強化学習の実力を実感できると思います。

実際にhuman_play.pyを実行したゲームプレイ画面は次のようになっています。ゲームサイズに合わせて、プレイヤーと敵（AI）も所持できる壁は１枚にしてあります。また、壁を置きたい場合は、下の「Place Wall」とクリックして、縦横方向を選んだ上で、置きたい場所（赤色の格子点）をクリックしてください。

初期状態

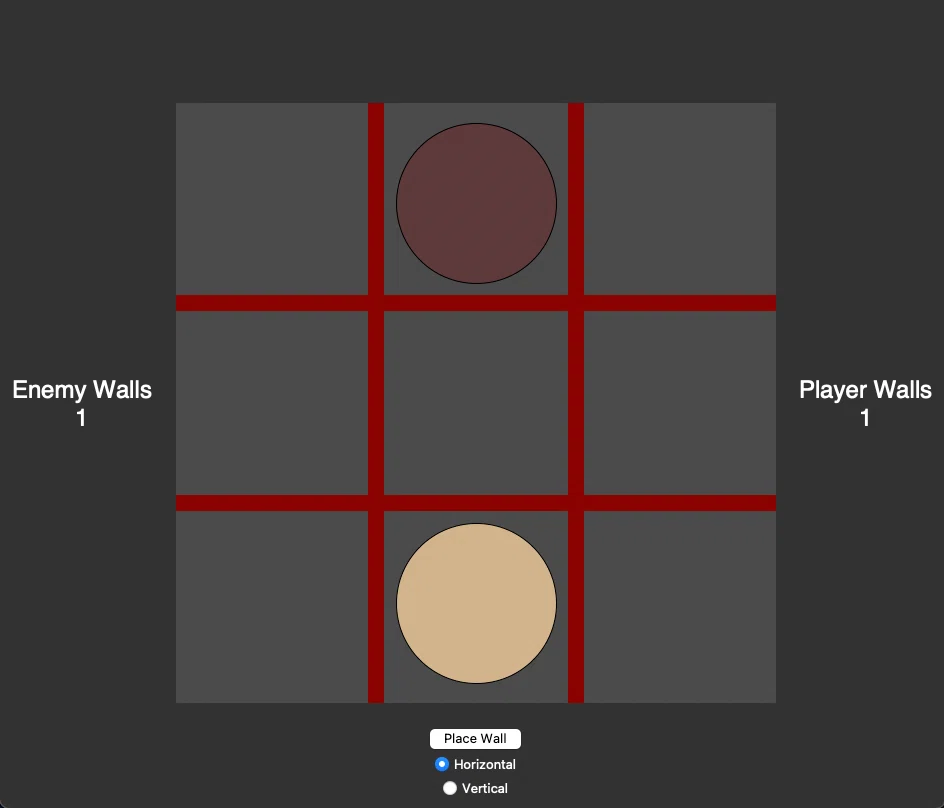
中盤戦

勝利した場合

敗北した場合

今回はあまり学習時間を多くとらなかったため、そこまで強いAIではなかったですが、より学習時間を長くすることでより強いAIができるでしょう。

まとめ

今回は、日本ではあまり馴染みのないボードゲームであるQuoridorに深層強化学習であるAlphaZeroを適用しました。基本的に二人ゼロ和有限確定完全情報ゲームであれば、ゲーム設計を変更するだけでどんなゲームでもAlphaZeroを適用することができますので、気になったゲームがあれば実装して、どのくらい強いAIができるかを試してみるのも面白いと思います。

もしも、この記事が面白かった方はいいねよろしくお願いします。また時間があれば何かしらの記事を書くかもしれません。

参考文献

[1] D. Silver et al., Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm.
[2] D. Silver et al., A General Reinforcement Learning Algorithm That Masters Chess, Shogi, and Go through Self-Play.
[3] K. He, X. Zhang, S. Ren, and J. Sun, Deep Residual Learning for Image Recognition.