⌛
【論文解説】HQ-VAE: 階層的な離散表現学習における確率的量子化（SQ）の導入

2025/03/10に公開
本記事では、以下の論文
で提案された、階層的離散表現学習モデル「HQ-VAE」を解説します。
機械学習、特に変分オートエンコーダ（VAE）、VQ-VAEの基礎知識はある程度前提としていますが、冒頭にて改めてまとめています。数式や専門用語が多く含まれますが、自作の図による解説と段階的な説明を通して理論を網羅することを目指しています。

この解説が、最新の生成モデル技術に興味をお持ちの方々の参考になれば幸いです。

 要約本論文では、階層的な離散潜在表現を学習する新たな変分オートエンコーダ (Variational Autoencoder; VAE) フレームワークである HQ-VAE が提案されている。
従来広く用いられてきた VQ-VAE 系列（VQ-VAE-2 や RQ-VAE など）は、離散コードブックを使って入力データを量子化し、高次元のデータ（画像や音声など）の圧縮や生成タスクに応用されてきた。しかし、これらの手法には

コードブック崩壊（コードブック要素が十分に活用されず、上位層がうまく機能しなくなる）、
重み付きハイパーパラメータ（ 𝛽 など）のチューニングやヒューリスティックな対処（Stop-Gradient, EMA 更新, コードブックリセットなど）が必要、
といった問題があった。
これに対し、本論文では「変分ベイズ」の枠組みに基づく階層的離散潜在表現学習を行う HQ-VAE を提案する。HQ-VAE は確率的量子化（Stochastic Quantization; SQ）を用いており、学習中に量子化過程が自己アニーリング的に「連続的→離散的」へ収束していくため、コードブックを効率的に使いながら安定した学習が可能になる。また、これにより従来必要とされてきた多数のハイパーパラメータ調整や EMA 更新といったヒューリスティックが不要になる利点が示されている。
さらに、従来の VQ-VAE-2、RQ-VAE などを HQ-VAE の特別な場合として位置付けられることから、既存の階層的離散表現手法を変分ベイズの観点で統一的に理解・拡張できる、といった貢献も強調されている。

 1. 導入
 1.1 VAEとVQ-VAE
 VAE (Variational AutoEncoder)
入力データを低次元の潜在空間へ圧縮し、そこから再構成を行う生成モデル。
潜在変数を確率分布として扱いながら、エンコーダとデコーダを同時に学習する。
高い柔軟性を持つ一方、再構成がぼやけやすいという欠点がある。
学習は、以下の変分下界（ELBO）の最大化により行う:

\text{ELBO:} \quad -\mathcal{J}_{\text{VAE}}
= \mathbb{E}_{q_{\bm{\phi}}(\boldsymbol{z}\mid\boldsymbol{x})}\bigl[\log p_{\bm{\theta}}(\boldsymbol{x}\mid\boldsymbol{z})\bigr]
- D_{\mathrm{KL}}\bigl(q_{\bm{\phi}}(\boldsymbol{z}\mid\boldsymbol{x}) \,\|\, p(\boldsymbol{z})\bigr).
ただし、

\boldsymbol{x}: 入力データ（観測変数）

\boldsymbol{z}: 潜在変数（低次元の特徴表現）

\bm{\phi}: エンコーダのパラメータ（\boldsymbol{x}から\boldsymbol{z}への変換を学習）

\bm{\theta}: デコーダのパラメータ（\boldsymbol{z}から\boldsymbol{x}の再構成を学習）

q_{\bm{\phi}}(\boldsymbol{z}\mid\boldsymbol{x}): 近似事後分布（エンコーダが出力）

p_{\bm{\theta}}(\boldsymbol{x}\mid\boldsymbol{z}): 尤度関数（デコーダが出力）

p(\boldsymbol{z}): 潜在変数の事前分布（通常は標準正規分布）

D_{\mathrm{KL}}: カルバック・ライブラー情報量（KLダイバージェンス）

 連続データに対するVAE\boldsymbol{x} が連続データの場合、通常VAEでは以下の確率分布を仮定する。
潜在変数の事前分布：p(\boldsymbol{z}) = \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})
標準正規分布（平均0、単位分散）
近似事後分布（エンコーダ出力）：q_{\bm{\phi}}(\boldsymbol{z}|\boldsymbol{x}) = \mathcal{N}(\boldsymbol{\mu}_{\bm{\phi}}(\boldsymbol{x}), \text{diag}(\boldsymbol{\sigma}^2_{\bm{\phi}}(\boldsymbol{x})))
対角共分散行列を持つ正規分布
生成モデル（デコーダ出力）：p_{\bm{\theta}}(\boldsymbol{x}|\boldsymbol{z}) = \mathcal{N}(\boldsymbol{\mu}_{\bm{\theta}}(\boldsymbol{z}), \sigma^2\boldsymbol{I})
固定分散\sigma^2を持つ等方性正規分布（単純化のため）
対数尤度項正規分布の確率密度関数の対数は、

\log p_{\bm{\theta}}(\boldsymbol{x}|\boldsymbol{z}) = -\frac{1}{2\sigma^2}||\boldsymbol{x} - \boldsymbol{\mu}_{\bm{\theta}}(\boldsymbol{z})||^2 - \frac{D}{2}\log(2\pi\sigma^2)
ここでDは入力データの次元数である。

定数項は無視できるので、この項は平均二乗誤差（MSE）に比例する。
KLダイバージェンス項二つの正規分布間のKLダイバージェンスは解析的に計算可能である。

\begin{aligned}
D_{\mathrm{KL}}\bigl(q_{\bm{\phi}}(\boldsymbol{z}|\boldsymbol{x}) \,\|\, p(\boldsymbol{z})\bigr) &= D_{\mathrm{KL}}\bigl(\mathcal{N}(\boldsymbol{\mu}_{\bm{\phi}}(\boldsymbol{x}), \text{diag}(\boldsymbol{\sigma}^2_{\bm{\phi}}(\boldsymbol{x}))) \,\|\, \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\bigr) \\
&= \frac{1}{2}\sum_{j=1}^{J} \left(\sigma^2_{\phi,j}(\boldsymbol{x}) + \mu^2_{\phi,j}(\boldsymbol{x}) - 1 - \log \sigma^2_{\phi,j}(\boldsymbol{x})\right)
\end{aligned}
ここで、Jは潜在変数の次元数である。
リパラメトリゼーション・トリック対数尤度の期待値を計算するために、リパラメトリゼーション・トリックを使用する。

\boldsymbol{z} = \boldsymbol{\mu}_{\bm{\phi}}(\boldsymbol{x}) + \boldsymbol{\sigma}_{\bm{\phi}}(\boldsymbol{x}) \odot \boldsymbol{\epsilon}, \quad \boldsymbol{\epsilon} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})
これにより、期待値を以下のように表現できる。

\mathbb{E}_{q_{\bm{\phi}}(\boldsymbol{z}|\boldsymbol{x})}\bigl[\log p_{\bm{\theta}}(\boldsymbol{x}|\boldsymbol{z})\bigr] = \mathbb{E}_{\boldsymbol{\epsilon} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})}\bigl[\log p_{\bm{\theta}}(\boldsymbol{x}|\boldsymbol{\mu}_{\bm{\phi}}(\boldsymbol{x}) + \boldsymbol{\sigma}_{\bm{\phi}}(\boldsymbol{x}) \odot \boldsymbol{\epsilon})\bigr]
以上より、連続データに対するVAEの目的関数\mathcal{J}_{\mathcal{N}-\text{VAE}}（マイナスELBO）は以下のように表される。

\begin{aligned}
&\mathcal{J}_{\mathcal{N}-\text{VAE}}(\boldsymbol{x}; \bm{\theta}, \bm{\phi}) \\
&(= -\text{ELBO}) \\
&= \frac{1}{2\sigma^2}||\boldsymbol{x} - \boldsymbol{\mu}_{\bm{\theta}}(\boldsymbol{\mu}_{\bm{\phi}}(\boldsymbol{x}))||^2 + \frac{1}{2\sigma^2}\text{Tr}(\boldsymbol{\Sigma}_{\bm{\theta}}(\boldsymbol{z}) \cdot \boldsymbol{\sigma}^2_{\bm{\phi}}(\boldsymbol{x})) \\
&+ \frac{1}{2}\sum_{j=1}^{J} \left(\sigma^2_{\phi,j}(\boldsymbol{x}) + \mu^2_{\phi,j}(\boldsymbol{x}) - 1 - \log \sigma^2_{\phi,j}(\boldsymbol{x})\right) + \frac{D}{2}\log(2\pi\sigma^2)
\end{aligned}
ここで、
第1項は平均的な再構成誤差
第2項はデコーダの勾配\boldsymbol{\Sigma}_{\bm{\theta}}(\boldsymbol{z})とエンコーダの不確かさ\boldsymbol{\sigma}^2_{\bm{\phi}}(\boldsymbol{x})の積のトレース（対角和）
第3項はエンコーダ出力の潜在分布と事前分布間のKLダイバージェンス
第4項は定数項（通常の最適化では分散 \sigma^2 を固定しているため）
なお、\boldsymbol{\Sigma}_{\bm{\theta}}(\boldsymbol{z})はデコーダ出力の平均\boldsymbol{\mu}_{\bm{\theta}}(\boldsymbol{z})に関するヤコビ行列の二次形式である。

実際の実装では、この項はしばしば無視されるか、単純化されて扱われる。
簡略化された一般的な形式では、目的関数は以下のように表される。

\mathcal{J}_{\mathcal{N}-\text{VAE}}(\boldsymbol{x}; \bm{\theta}, \bm{\phi}) = \frac{1}{2\sigma^2}||\boldsymbol{x} - \boldsymbol{\mu}_{\bm{\theta}}(\boldsymbol{\mu}_{\bm{\phi}}(\boldsymbol{x}))||^2 + \frac{1}{2}\sum_{j=1}^{J} \left(\sigma^2_{\phi,j}(\boldsymbol{x}) + \mu^2_{\phi,j}(\boldsymbol{x}) - 1 - \log \sigma^2_{\phi,j}(\boldsymbol{x})\right)
この形式は「再構成誤差 + KL正則化項」という直感的な解釈が可能である。
なお、以降で扱うモデルも同様に \boldsymbol{x} は正規分布に従う連続データと仮定する。

 VQ-VAE (Vector Quantized VAE)
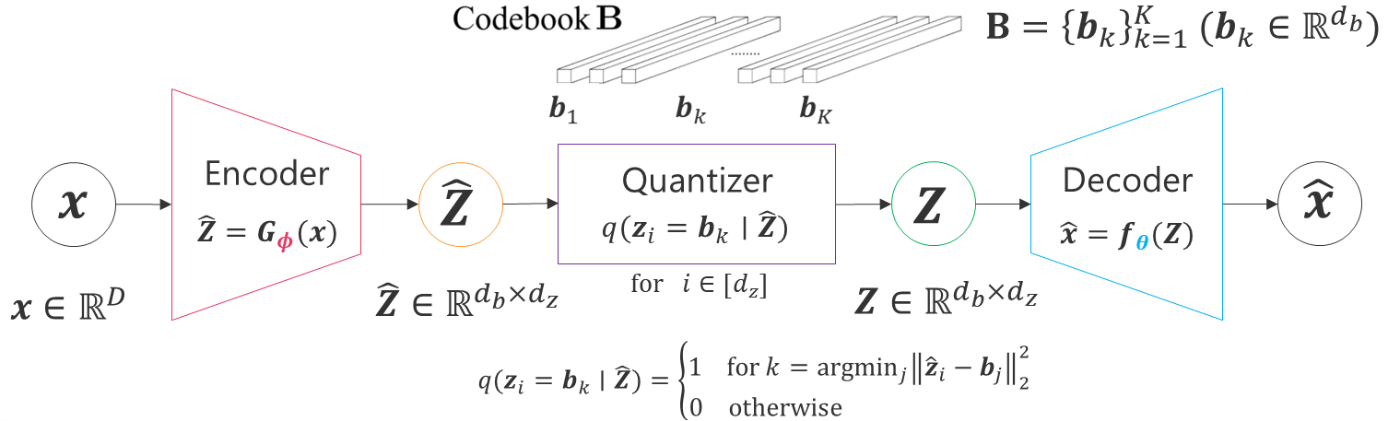
潜在空間を離散化し、コードブック上の埋め込みベクトルを使って表現することで、シャープな画像生成や離散表現の学習が可能に。
「入力特徴を最も近い埋め込みベクトルへ量子化→再構成」する仕組み。
典型的な目的関数は以下のように書かれる（\mathrm{sg}[\cdot] は勾配停止演算の省略記号）:

\mathcal{J}_{\text{VQ-VAE}}(\boldsymbol{x}; \bm{\theta}, \bm{\phi},\bm{B})
= \bigl\|\boldsymbol{x} - \bm{f}_{\bm{\theta}}(\boldsymbol{Z})\bigr\|_{2}^{2} 
+ \bigl\|\mathrm{sg}[\hat{\boldsymbol{Z}}] - \boldsymbol{Z}\bigr\|_{F}^{2}
+ \beta\,\bigl\|\hat{\boldsymbol{Z}} - \mathrm{sg}[\boldsymbol{Z}]\bigr\|_{F}^{2}.
ただし、

\boldsymbol{x}: 入力データ

\hat{\boldsymbol{Z}} (=\bm{G}_{\bm{\phi}}(\boldsymbol{x})): エンコーダ出力（量子化前の連続的な潜在表現）

\boldsymbol{Z}: 量子化後の離散的な潜在表現（コードブックから選択された埋め込みベクトル）

\bm{f}_{\bm{\theta}}: デコーダ関数

\bm{\theta}: デコーダのパラメータ

\|\cdot\|_2: ユークリッドノルム（L2ノルム）

\|\cdot\|_F: フロベニウスノルム（行列のノルム）

\beta: コミットメント損失の重み係数（ハイパーパラメータ）

\mathrm{sg}[\cdot]: 勾配停止演算子（逆伝播時に勾配を流さない）
一方、学習が進むと「コードブックの一部しか使われなくなる（コードブック崩壊）」が生じやすいのが難点。

 1.2 階層版VQ-VAE
 VQ-VAE-2

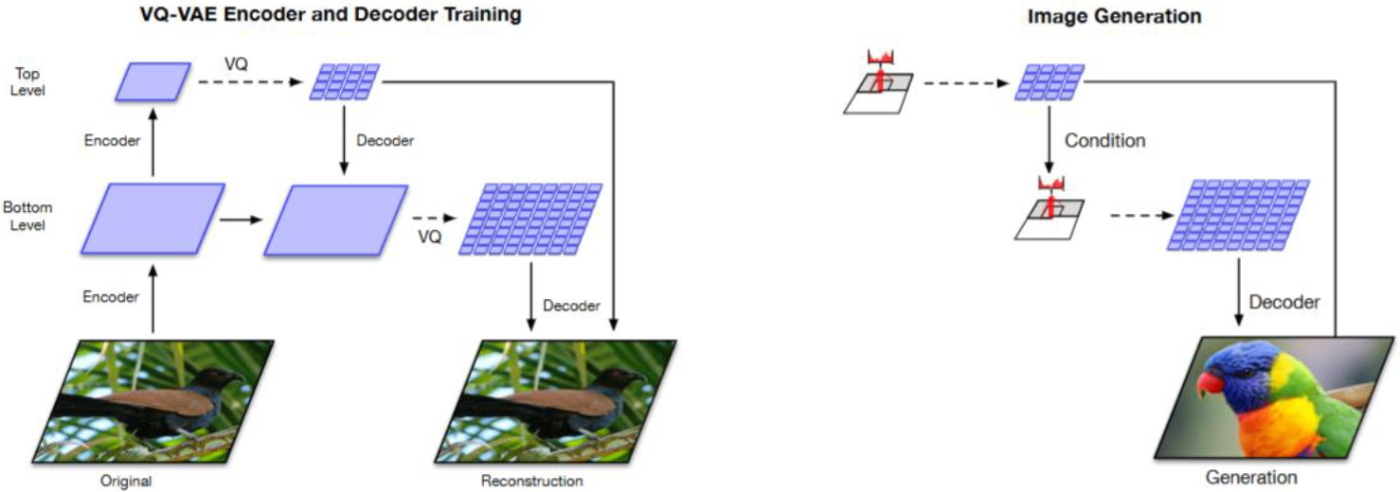
VQ-VAE-2は、VQ-VAEに階層的な離散潜在空間を導入したモデル。従来のVQ-VAEが単一のコードブックのみを扱うのに対し、複数レベル（上位層・下位層）のコードブックを用いて、異なる解像度・粒度の情報を表現する。

トップレベル（上位層）
画像全体の大まかな構造を量子化し、グローバルな色や形を表現。


ボトムレベル（下位層）
トップレベルではカバーしきれない細部の情報を量子化し、テクスチャなど局所的特徴を表現。


 トップダウンとボトムアップ
ボトムアップのエンコーダ

入力画像から下位層の特徴マップを得て、それをさらにダウンサンプリングして上位層の特徴マップを導出。両層で量子化を実施。

トップダウンのデコーダ

上位層のコードから大まかな構造を復元し、下位層のコードを追加して細部を再現。

 学習方法VQ-VAEで用いられる勾配停止やEMA更新を階層的に適用。
しかし階層が増えることで、特定の層だけがほぼ使われないなどのコードブック崩壊が起こりやすい点が指摘されている。

 特徴・メリット
高解像度生成: 層を増やすほど細部を捉えやすくなるため、単層VQ-VAEより高精細な画像を生成しやすい。

グローバルとローカルの分離: 上位層で大きな構造、下位層で細部を学習するため、解釈性や編集応用がしやすい。

 目的関数
\mathcal{J}_{\text{VQ-VAE-2}}(\boldsymbol{x}; \bm{\theta}, \bm{\phi},\mathcal{B}) = \|\boldsymbol{x} - \bm{f}_{\bm{\theta}}(\boldsymbol{Z}_{1:L})\|_2^2 + \beta \sum_{l=1}^L \|\bm{G}_{\bm{\phi}_l}(\boldsymbol{x}, \boldsymbol{Z}_{1:l-1}) - \text{sg}[\boldsymbol{Z}_l]\|_F^2
ここで、

\boldsymbol{x}は入力データ

\bm{G}_{\bm{\phi}_l}はl番目の層のエンコーダ関数（パラメータ\bm{\phi}_lを持つ）

\bm{\phi} = (\bm{\phi}_1, \ldots, \bm{\phi}_L): 階層的エンコーダのパラメータセット

\bm{f}_{\bm{\theta}}はデコーダ関数

\bm{\theta}はデコーダのパラメータ

\mathcal{B} = \{\mathbf{B}_1, \mathbf{B}_2, ..., \mathbf{B}_L\} は各層 l に対応するコードブック \mathbf{B}_l の集合

\boldsymbol{Z}_{1:L}は全層の量子化後の潜在表現

（L=2の場合、\boldsymbol{Z}_1 = \boldsymbol{Z}_{top}、\boldsymbol{Z}_2 = \boldsymbol{Z}_{bottom}）

\hat{\boldsymbol{Z}}_l(=\bm{G}_{\bm{\phi}_l}(\boldsymbol{x}, \boldsymbol{Z}_{1:l-1}))はl番目の層のエンコーダの出力（階層lでの量子化前の連続的な潜在表現）

\|\cdot\|_2はユークリッドノルム

\|\cdot\|_Fはフロベニウスノルム

\betaはコミットメント損失の重み係数

\text{sg}[\cdot]は勾配停止演算子
第1項は再構成誤差、第2項はコミットメント損失。

 RQ-VAE (Residual-Quantized VAE)

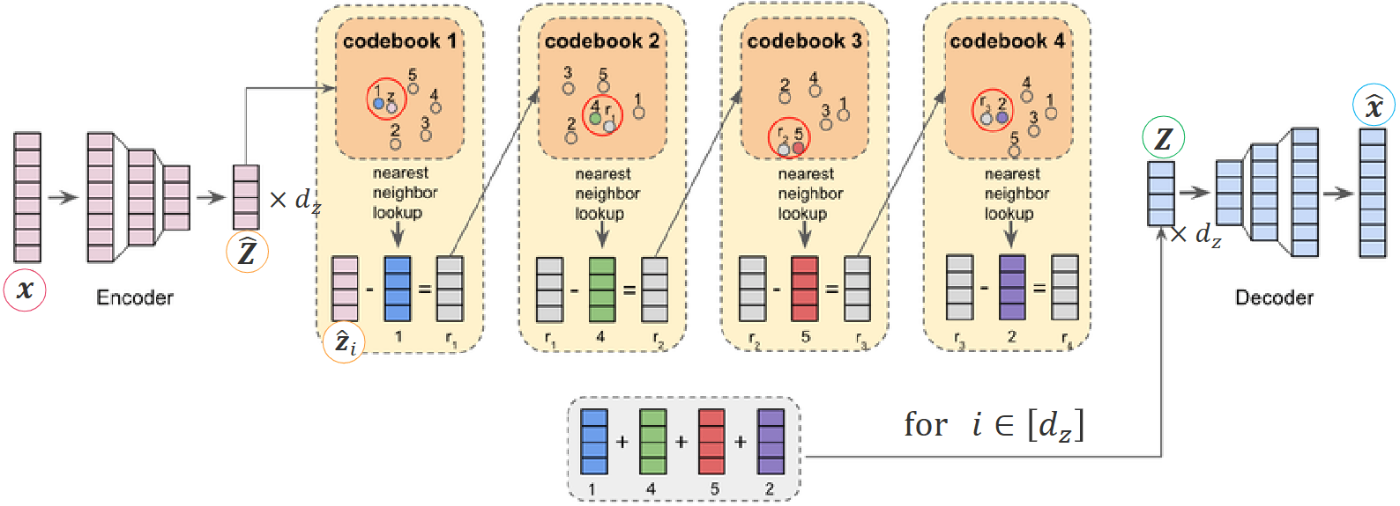
RQ-VAEは「残差を再量子化する」手法で階層化を実現。VQ-VAE-2のように解像度で階層を分けるのではなく、「粗→細」と段階的に情報を補完する。

1層目の量子化: 入力特徴マップをコードブックで量子化し、大まかな近似を得る。

残差計算: 「元の特徴マップ − 量子化後の近似」を取り、取りこぼした情報を抽出。

2層目量子化: その残差を別コードブックで量子化し、より細かい補正を与える。

必要に応じて繰り返し: 粗い表現から徐々に残差を埋めることで、多層的に情報をカバー。

 コードブックの「実質的サイズ」を拡大1層あたりのコードブックサイズがKでも、L層積めば最大でK^L通りの表現組合せが可能。
段階的に学習できるため、大規模コードブックを直接学習するより崩壊を緩和しやすい面もあるが、やはり崩壊は起こりうる。

 特徴・メリット
柔軟性: 残差を少しずつ埋めていく構造のため、拡張が容易。

層追加による表現力向上: 追加の層でさらなるビットレート・解像度を実現できる。

 目的関数RQ-VAEの目的関数は、複数の残差量子化層を考慮した形で表現される。

\mathcal{J}_{\text{RQ-VAE}}(\boldsymbol{x}; \bm{\theta}, \bm{\phi},\mathcal{B}) = \|\boldsymbol{x} - \bm{f}_{\bm{\theta}}(\boldsymbol{Z})\|_2^2 + \beta \sum_{l=1}^{L} \|\bm{H}_{\boldsymbol{\phi}}(\boldsymbol{x}) - \mathrm{sg}[\sum_{l'=1}^{l} \boldsymbol{Z}_{l'}]\|_{F}^{2}
ここで、

\boldsymbol{x}は入力データ

\boldsymbol{Z}_lは階層lの量子化残差(量子化した\tilde{\boldsymbol{Z}}_l)

\hat{\boldsymbol{Z}}_l(=\bm{H}_{\boldsymbol{\phi}}(\boldsymbol{x}) - \sum_{l'=1}^{l-1} \boldsymbol{Z}_{l'})はl回目の(量子化前の)残差
なお、\hat{\boldsymbol{Z}}_1 = \bm{H}_{\boldsymbol{\phi}}(\boldsymbol{x})と定める


\boldsymbol{Z}(=\sum_{l=1}^{L} \boldsymbol{Z}_{l})は最終的な潜在表現

\hat{\boldsymbol{Z}} (=\bm{H}_{\boldsymbol{\phi}}(\boldsymbol{x}))はエンコーダの出力

\bm{f}_{\bm{\theta}}はデコーダ関数

\bm{\theta}はデコーダのパラメータ

\mathcal{B} = \{\mathbf{B}_1, \mathbf{B}_2, ..., \mathbf{B}_L\} は各層 l に対応するコードブック \mathbf{B}_l の集合

\|\cdot\|_2はユークリッドノルム

\|\cdot\|_Fはフロベニウスノルム

\betaはコミットメント損失の重み係数

\mathrm{sg}[\cdot]は勾配停止演算子

 VQ-VAE-2とRQ-VAEの比較階層の設計

VQ-VAE-2: グローバル→局所という形で解像度別に階層を分ける。

RQ-VAE: 前層の残差を次層で量子化し、粗→細へと精緻化。
コードブックの解釈

VQ-VAE-2: 上位層が大まかな形状、下位層がテクスチャなど、役割が比較的明確に分かれる。

RQ-VAE: 残差を補っていくため、層ごとの意味分担は必ずしも明瞭ではないが、積むほど表現力が増す。

 1.3 VQのコードブック崩壊と対策VQ-VAEでのコードブック崩壊

学習が進むほどに一部のコードブック要素だけが使われる問題。表現の偏りや再構成精度の低下をもたらす。
ヒューリスティクスでの対策

EMA (Exponential Moving Average) による埋め込みベクトル更新
使用率が低いコードブック要素のリセット
ハイパーパラメータ調整
階層版VQ-VAEでの崩壊
複数階層が絡むため、「VQ-VAE-2では上位層が一部の表現しか使われない」「RQ-VAEでは下位層が一部の表現しか使われない」などの形でコードブック崩壊が発生しやすい。

 1.4 VQからSQ（確率的量子化）へ
従来の決定論的量子化では「最も近い埋め込みベクトル」を一意に選択していた:

q\bigl(\bm{z}_i = \bm{b}_k \mid \hat{\bm{Z}}\bigr)
= 
\begin{cases}
1 & \text{if } k = \operatorname{argmin}_{j}\|\hat{\bm{z}}_i - \bm{b}_j\|_{2}^{2},\\
0 & \text{otherwise}.
\end{cases}
一方、SQ (Stochastic Quantization) では確率的に選択することで、表現選択の極端な偏りを回避しやすくする:

\hat{p}_{s^{2}}\bigl(\bm{z}_i = \bm{b}_k \mid \hat{\bm{Z}}\bigr)
\propto \exp\Bigl(-\frac{\|\hat{\bm{z}}_i - \bm{b}_k\|_{2}^{2}}{2s^{2}}\Bigr).
このSQを変分ベイズの枠組みを用いてVQ-VAEに自然に導入したのが、次に紹介するSQ-VAEである。

 SQ-VAE (Stochastically Quantized VAE)
VQ-VAEをSQ化することで、コードブック崩壊を緩和。
確率的な量子化を徐々に決定論的に収束させる「セルフアニーリング効果」を利用。
従来のヒューリスティクスをほぼ不要にし、ハイパーパラメータも1種類に削減。
学習は以下に示すELBOの最大化により行われる。

\begin{aligned}
\log p_{\bm{\theta}}(\bm{x}) &\ge 
\mathbb{E}_{q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})\hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}})}\left[
\log \frac{p_{\bm{\theta}}(\bm{x}|\tilde{\bm{Z}})\,p_{\bm{\varphi}}(\tilde{\bm{Z}}|\bm{Z})\,P(\bm{Z})}{q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})\,\hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}})}
\right] \\[8pt]
&=\mathbb{E}_{q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})\,\hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}})}\left[
\log \frac{p_{\bm{\theta}}(\bm{x}|\bm{Z})\,p_{\bm{\varphi}}(\tilde{\bm{Z}}|\bm{Z})}{q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})}
\right] + \mathbb{E}_{q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})} \Bigl[ H\bigl(\hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}})\bigr) \Bigr] + \text{const.}
\end{aligned}

 変数：
\bm{x}: 入力データ

\hat{\bm{Z}}:= \bm{G_\phi}(\bm{x}) "小さな"エンコーダが決定論的に出す潜在変数

\tilde{\bm{Z}}\bigl(\sim \mathcal{N}(\hat{\bm{Z}};\,\bm{Z},\,s^2 \boldsymbol{I})\bigr): 連続潜在変数（\hat{\bm{Z}}が脱量子化された潜在変数）

\bm{Z}: 離散潜在変数（量子化された潜在変数）

H(\cdot): エントロピー

 確率分布：
q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x}) は"大きな"エンコーダ、または近似事後全体 (\bm{x} \to \tilde{\bm{Z}})

p_{\bm{\varphi}}(\tilde{\bm{Z}}|\bm{Z}) は脱量子化過程に対応する分布 (\bm{Z} \to \tilde{\bm{Z}})

P(\bm{Z}) は事前分布

\hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}}) は量子化過程に対応する分布（確率質量）(\tilde{\bm{Z}} \to \bm{Z})

p_{\bm{\theta}}(\bm{x}|\bm{Z}) はデコーダ (\bm{Z} \to \bm{x})
※ "小さな"エンコーダ \bm{G_\phi}(\cdot) は、決定論的に \bm{x} → \hat{\bm{Z}} とするが、"大きな"エンコーダ q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x}) は、決定論的射影＋脱量子化をし、\bm{x} → \hat{\bm{Z}} → \tilde{\bm{Z}} とする。

 パラメータ：
\bm{\theta}: デコーダのパラメータ

\bm{\phi}: エンコーダのメインパラメータ

\bm{\varphi}: 量子化/脱量子化過程のパラメータ

(\bm{\phi}, \bm{\varphi}): エンコーダのパラメータセット全体
なおこの導出で、一様事前分布（P(\bm{Z})=1/K, K: 量子化コードブックのサイズ）の仮定から、

\begin{aligned}
\text{KL}\bigl(\hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}})\,\|\,P(\bm{Z})\bigr) 
&= \mathbb{E}_{\hat{P}_{\bm{\varphi}}}\left[\log\frac{\hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}})}{P(\bm{Z})}\right] \\[6pt]
&= \mathbb{E}_{\hat{P}_{\bm{\varphi}}}\left[\log \hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}})\right] - \log\frac{1}{K} \\[6pt]
&= -H(\hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}})) + \text{const.}
\end{aligned}
を利用した。
生成過程に等方性正規分布を仮定する生成過程の尤度を以下のように仮定する。

p_{\bm{\theta}}(\bm{x}|\bm{Z}) = \mathcal{N}(\bm{x};\,\mu_{\bm{\theta}}(\bm{Z}),\,\sigma^2 \boldsymbol{I})
ここで、

\mu_{\bm{\theta}}(\bm{Z}) は潜在変数 \bm{Z} から計算される平均ベクトル

\sigma^2 はスカラーであり、学習可能な分散パラメータである。

\bm{\theta} はデコーダのパラメータ
その対数尤度は次のようになる。

\begin{aligned}
\log p_{\bm{\theta}}(\bm{x}|\bm{Z})
&= -\frac{1}{2}\left[
D \log(2\pi\sigma^2) 
+ \frac{1}{\sigma^2}\|\bm{x} - \mu_{\bm{\theta}}(\bm{Z})\|^2
\right] \\
&= -\frac{D}{2} \log\sigma^2 
- \frac{1}{2\sigma^2}\|\bm{x} - \mu_{\bm{\theta}}(\bm{Z})\|^2
+ \text{const.}
\end{aligned}
ここで D は観測変数 \bm{x} の次元を表す。
脱量子化過程に（等方性）正規分布を仮定するSQ-VAEのELBO一般式のうち、

\begin{aligned}
\log \frac{p_{\bm{\varphi}}(\tilde{\bm{Z}}|\bm{Z})}{q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})}
&= \log p_{\bm{\varphi}}(\tilde{\bm{Z}}|\bm{Z}) - \log q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})
\end{aligned}.
この部分について考える。

従来どおり、脱量子化は正規分布と仮定する。すなわち、

p_{\bm{\varphi}}(\tilde{\bm{Z}}|\bm{Z}) = \mathcal{N}\Bigl(\tilde{\bm{Z}};\,\mu_{\bm{\varphi}}(\bm{Z}),\,\Sigma_{\bm{\varphi}}\Bigr).
その対数は、

\log p_{\bm{\varphi}}(\tilde{\bm{Z}}|\bm{Z})
= -\frac{1}{2}\left[\log \bigl|2\pi\Sigma_{\bm{\varphi}}\bigr| + (\tilde{\bm{Z}}-\mu_{\bm{\varphi}}(\bm{Z}))^\top\Sigma_{\bm{\varphi}}^{-1}(\tilde{\bm{Z}}-\mu_{\bm{\varphi}}(\bm{Z}))\right].
同様に、エンコードも内部で同じ脱量子化過程を含む。つまり、

p_{\bm{\varphi}}(\tilde{\bm{Z}}|\hat{\bm{Z}}) = \mathcal{N}\Bigl(\tilde{\bm{Z}};\,\mu_{\bm{\varphi}}(\hat{\bm{Z}}),\,\Sigma_{\bm{\varphi}}\Bigr).
よって、

\begin{aligned}
\log q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})
&= \log q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|g_{\bm{\phi}}(\bm{x})) \\[6pt]
&= \log q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\mu_{\bm{\varphi}}(\hat{\bm{Z}})) \\[6pt]
&= -\frac{1}{2}\left[ \log \bigl|2\pi\Sigma_{\bm{\varphi}}\bigr| + \bigl(\tilde{\bm{Z}} - \mu_{\bm{\varphi}}(\hat{\bm{Z}})\bigr)^\top \Sigma_{\bm{\varphi}}^{-1}\bigl(\tilde{\bm{Z}} - \mu_{\bm{\varphi}}(\hat{\bm{Z}})\bigr)\right].
\end{aligned}
次に \log p_{\bm{\varphi}}(\tilde{\bm{Z}}|\bm{Z}) - \log q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x}) を考えると、まず \log \bigl|2\pi\Sigma_{\bm{\varphi}}\bigr| が相殺されて消える。

残った二次形式の項のうち、2番目に導出した方の期待値は、

\begin{aligned}
&\frac{1}{2}\mathbb{E}_{q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})}
\left[
(\tilde{\bm{Z}} - g_{\bm{\phi}}(\bm{x}))^\top\Sigma_{\bm{\varphi}}^{-1}(\tilde{\bm{Z}} - g_{\bm{\phi}}(\bm{x}))
\right] \\
&= \sum_{i=1}^{d_z}
\underbrace{
\frac12 \;
E_{p_{\bm{\varphi}}(\bm{Z} \mid g_{\bm{\phi}}(\bm{x}))}
\bigl[(z_i - g_{\bm{\phi}}(\bm{x})_i)^\top\Sigma_{\bm{\varphi}}^{-1}(z_i - g_{\bm{\phi}}(\bm{x})_i)\bigr]
}_{=\,d_b/2} \\
&= \frac{d_b\,d_z}{2} \\
&= \text{const.}
\end{aligned}
となり消える。（\mu_{\bm{\varphi}}(\hat{\bm{Z}})=g_{\bm{\phi}}(\bm{x}) に注意）
なお、(z_i - g_{\bm{\phi}}(\bm{x})_i)^\top\Sigma_{\bm{\varphi}}^{-1}(z_i - g_{\bm{\phi}}(\bm{x})_i) は多変量正規分布におけるマハラノビス距離の二乗を表し、カイ二乗分布（自由度 d_b）に従う。
そのため、この項の期待値はカイ二乗分布の性質から自由度に等しくなり、結果として d_b と求まる。
以上より、最終的に期待値の中で残るのは、

- \frac{1}{2} (\tilde{\bm{Z}}-\mu_{\bm{\varphi}}(\bm{Z}))^\top\Sigma_{\bm{\varphi}}^{-1}(\tilde{\bm{Z}}-\mu_{\bm{\varphi}}(\bm{Z}))
という項だけである。

 Gaussian Ⅰ SQ-VAEの場合脱量子化過程の正規分布にさらに等方性共分散行列の仮定を導入すると、

p_{\bm{\varphi}}(\tilde{\bm{Z}}|\bm{Z}) 
= \mathcal{N}(\tilde{\bm{Z}};\,\bm{Z},\,s^2 \boldsymbol{I})
となる。ここで s^2 は \bm{\varphi} の一部として扱われるパラメータである。

要するに\Sigma_{\bm{\varphi}} = s^2 \boldsymbol{I}となるため、期待値の中に最終的に残る項は以下のように書ける。

-\frac{1}{2s^2}\|\tilde{\bm{Z}} - \bm{Z}\|_{F}^2
ここで、

\tilde{\bm{Z}} はエンコーダによる潜在変数（量子化前の連続的な潜在変数）

\bm{Z} は量子化後の潜在変数（離散表現）

s^2 は脱量子化分布の分散（スカラー）、\bm{\varphi} の一部
以上の簡略化により、項が直観的に潜在変数の量子化前後の距離（二乗誤差）に比例した形で表されることが明らかとなる。

 Gaussian Ⅰ SQ-VAEの場合確率分布の仮定を用いてELBOベースの目的関数を計算すると、

\begin{aligned}
&\mathcal{J}_{{\mathcal{N}_1}-\text{SQ-VAE}}(\bm{x};\bm{\theta},\bm{\phi},\sigma^2,s^{2},\mathbf{B}) \\
&= \frac{D}{2}\log\sigma^{2}
+ \mathbb{E}_{q_{(\bm{\phi},\bm{\varphi})}(\tilde{\bm{Z}}|\bm{x})\hat{P}_{\bm{\varphi}}(\bm{Z}|\tilde{\bm{Z}})}
\Biggl[
\frac{\|\bm{x}-\bm{f}_{\bm{\theta}}(\bm{Z})\|_{2}^{2}}{2\sigma^{2}}
+ \frac{\|\tilde{\bm{Z}}-\bm{Z}\|_{F}^{2}}{2s^{2}}
- H\bigl(\hat{P}_{s^{2}}(\bm{Z}\mid \tilde{\bm{Z}})\bigr)
\Biggr]
\end{aligned}
この式は以下の要素で構成されている。
再構成誤差項: \frac{D}{2}\log\sigma^{2} + \frac{\|\bm{x}-\bm{f}_{\bm{\theta}}(\bm{Z})\|_{2}^{2}}{2\sigma^{2}}
量子化誤差項: \frac{\|\tilde{\bm{Z}}-\bm{Z}\|_{F}^{2}}{2s^{2}}
エントロピー(のマイナス倍)項: -H\bigl(\hat{P}_{s^{2}}(\bm{Z}\mid \tilde{\bm{Z}})\bigr)

 1.5 階層版VQ-VAEもSQ化したい → HQ-VAEの提案

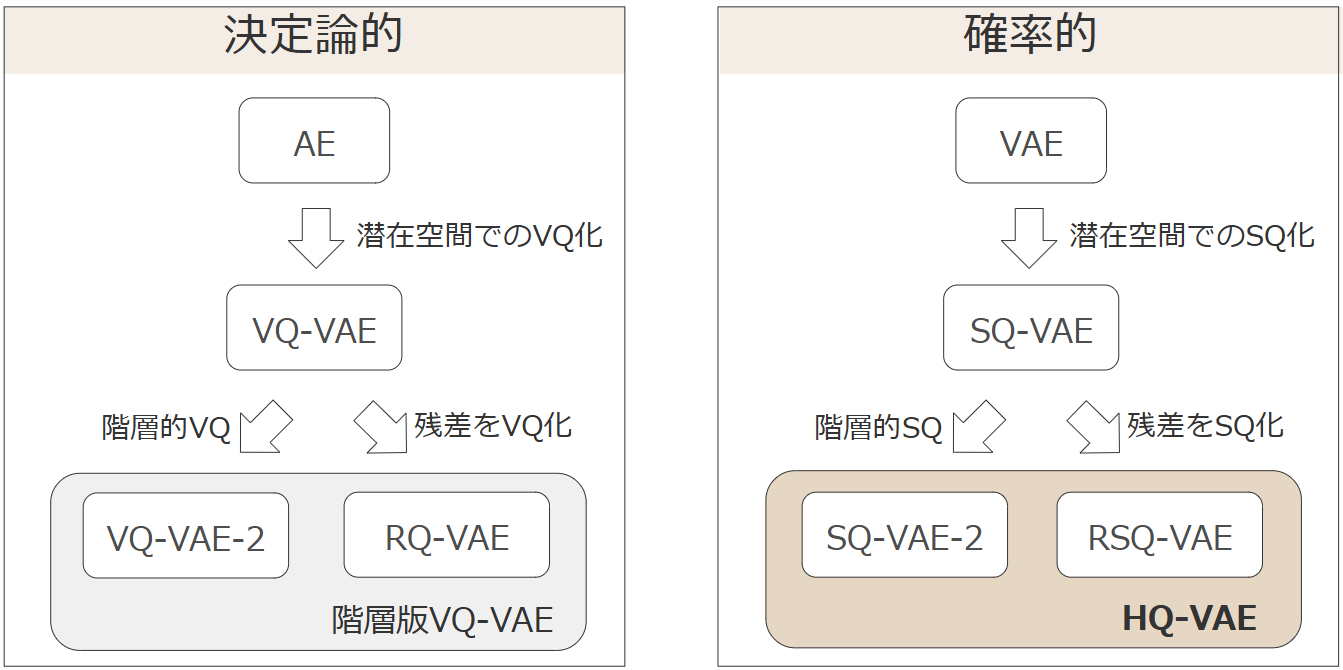
 2. 提案手法: HQ-VAE
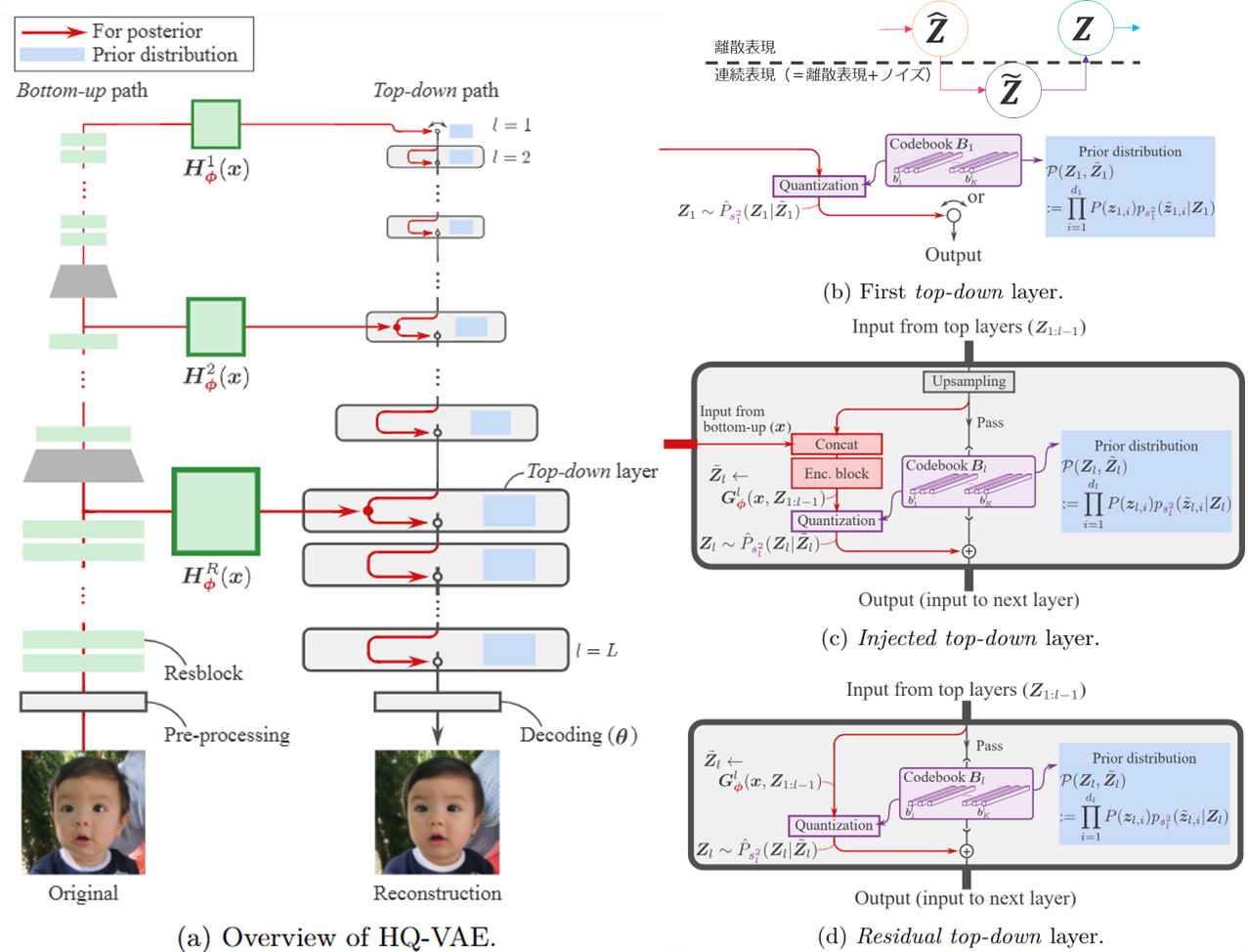
HQ-VAEは、階層的に離散潜在変数を扱う変分ベイズモデルで、各階層に確率的量子化(SQ)を導入し、コードブック崩壊を抑制する。以下、各構成要素を順を追って見ていく。

 2.1 階層的離散表現階層構造

潜在変数を \bm{Z}_{1:L} とし、各階層 l にコードブック \mathbf{B}_l（埋め込み数 K_l、次元 d_l）を設定。
事前分布と生成

各階層の潜在変数は一様事前分布 P(\boldsymbol{z}_{l,i} = \boldsymbol{b}_k) = 1/K_l を仮定し、生成モデルは等方性正規分布

  p_{\bm{\theta}}(\boldsymbol{x} \mid \bm{Z}_{1:L})
  = \mathcal{N}\bigl(\boldsymbol{x};\, \bm{f}_{\bm{\theta}}(\bm{Z}_{1:L}),\, \sigma^{2}\mathbf{I}\bigr).
  
変分推論

真の事後分布 p_{\bm{\theta}}(\mathbf{Z}_{1:L}\mid x) は計算困難なので、近似事後を導入し、ELBOの最大化により学習を行う。

 2.2 トップダウン層の構成HQ-VAEでは、トップダウン方向の情報伝達を行う層として下記の3種類を定義している。
Firstトップダウン層

全HQ-VAEインスタンスに必ず存在する最上位層。
これのみの構成は単層のSQ-VAEに相当。
Injected型トップダウン層

ボトムアップパスの高解像度特徴を「注入」し、VQ-VAE-2的な「グローバル情報→局所情報」の構造を実現。
Residual型トップダウン層

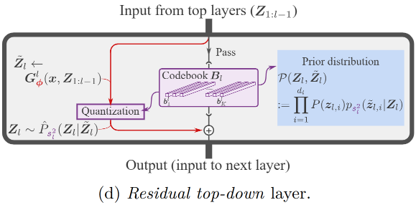
一つ前の階層で量子化した残差をさらに量子化して補完する。RQ-VAEに相当。
これらを自在に組み合わせることで、任意の階層設計を行える。

 2.3 DequantizationとQuantization各階層 l における逆量子化 (Dequantization) は等方性正規分布を仮定し、量子化 (Quantization) はベイズの定理に基づいて

\hat{P}_{s_l^2}(\boldsymbol{z}_{l, i} = \boldsymbol{b}_k \mid \tilde{\boldsymbol{Z}}_l)
\propto \exp\Bigl(-\frac{\|\tilde{\boldsymbol{z}}_{l,i} - \boldsymbol{b}_k\|_{2}^{2}}{2s_l^{2}}\Bigr).
と表される。

補助変数 \tilde{\bm{Z}}_{1:L} を導入した変分下界（ELBO）の最大化によって、階層ごとの確率的量子化が学習される仕組みである。

 3. HQ-VAEのインスタンスと実験結果トップダウン層の構成によって、大きく2種類のHQ-VAEインスタンスが示されている。

 3.1 SQ-VAE-2 (Injected Top-Down Only)概要

Injected型トップダウン層のみを用いた、VQ-VAE-2のSQ版に相当するモデル。
損失関数

以下のELBOベースの目的関数を最小化することで学習を行う。

    \begin{aligned}
    &\mathcal{J}_{\text{SQ-VAE-2}}(\bm{x};\bm{\theta},\bm{\phi},\sigma^2,\bm{s}^{2},\mathcal{B}) \\
    &= \frac{D}{2}\log\sigma^{2}
    + \mathbb{E}_{\mathcal{Q}(\bm{Z}_{1:L}, \tilde{\bm{Z}}_{1:L}\mid \bm{x})}
    \Biggl[
    \frac{\|\bm{x}-\bm{f}_{\bm{\theta}}(\bm{Z}_{1:L})\|_{2}^{2}}{2\sigma^{2}}
    + \sum_{l=1}^{L}
      \Bigl(
        \frac{\|\tilde{\bm{Z}}_{l}-\bm{Z}_{l}\|_{F}^{2}}{2s_{l}^{2}}
        - H\bigl(\hat{P}_{s_{l}^{2}}(\bm{Z}_{l}\mid \tilde{\bm{Z}}_{l})\bigr)
      \Bigr)
    \Biggr].
    \end{aligned}
    ここで \bm{s}^2 = (s_1^2, \ldots, s_L^2) は各層 l に対応するパラメータ s_l^2 をまとめたベクトルを表す。

また \mathcal{B} = \{\mathbf{B}_1, \mathbf{B}_2, ..., \mathbf{B}_L\} は各層 l に対応するコードブック \mathbf{B}_l の集合を表現している。
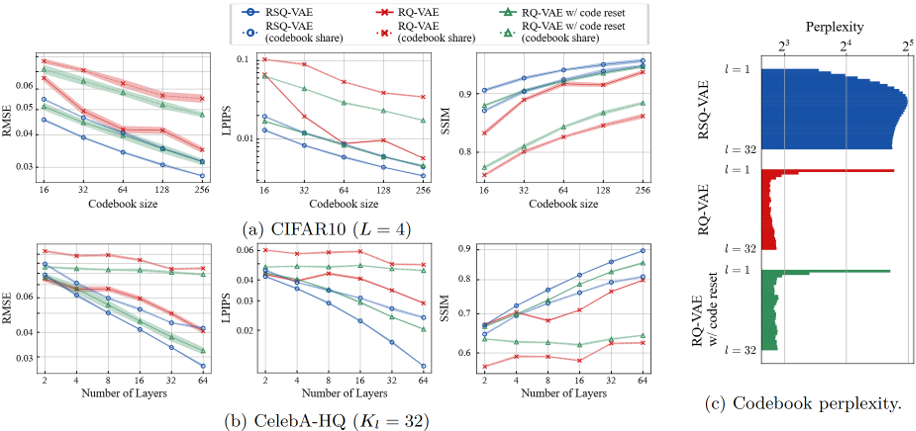
実験結果

再構成性能はVQ-VAE-2を大きく上回り、特に下位層のコードブック使用率が高まることが報告されている。


Dataset
Model
RMSE ↓
LPIPS ↓
SSIM ↑
exp(H(Q(Z₁)))
exp(H(Q(Z₂)))
...


ImageNet
VQ-VAE-2
6.071
0.265
0.751
106.8
288.8



SQ-VAE-2
4.603
0.096
0.855
406.2
355.5


FFHQ
VQ-VAE-2
4.866
0.323
0.814
24.6
41.3
...


SQ-VAE-2
2.118
0.166
0.909
125.8
398.7
...


 3.2 RSQ-VAE (Residual Top-Down Only)概要

Residual型トップダウン層のみで構成した、RQ-VAEのSQ版。
特徴
RQ-VAEより高い再構成性能を達成。
上位層のコードブック使用率が特に向上することが確認。
損失関数

素直にELBOベースの目的関数を導出すると以下のようになる。

  \begin{aligned}
  &\mathcal{J}_{\text{RSQ-VAE}}^{\text{naïve}}(\bm{x};\bm{\theta},\bm{\phi},\sigma^2,\bm{s}^{2},\mathcal{B}) \\
  &= \frac{D}{2}\log\sigma^2 + \mathbb{E}_{Q(\bm{Z}_{1:L},\tilde{\bm{Z}}_{1:L}|x)}\Biggl[\frac{\|\bm{x} - \bm{f}_{\bm{\theta}}(\bm{Z}_{1:L})\|_2^2}{2\sigma^2} + \sum_{l=1}^{L}\Bigl(\frac{\|\tilde{\bm{Z}}_l - \bm{Z}_l\|_F^2}{2s_l^2} - H(\hat{P}_{s_l^2}({\bm{Z}}_l|\tilde{\bm{Z}}_l))\Bigr)\Biggr]
  \end{aligned}
  しかし、この目的関数では訓練が不安定になる問題があった。

原因は、全ての l \in [L] に対して \sum_{l'=1}^{l}\bm{Z}_{l'} を一律にエンコーダの出力 \bm{H}_{\boldsymbol{\phi}}(\boldsymbol{x}) に近づけるよう正則化することで、上位層(l の小さい層)に過度に情報が押し込まれ、下位層(l の大きい層)での層崩壊を引き起こす可能性がある。
そこで潜在変数の正則化を弱めるために、以下のような仮定の変更を行う。
新たな仮定と変更点
潜在変数 \bm{Z}_{1:L} の事前分布 \mathcal{P} を変更し、弱い正則化を導入。
具体的には、事前分布を (\bm{Z}_{1:L}, \tilde{\bm{Z}}_{1:L}) ではなく (\bm{Z}_{1:L}, \tilde{\bm{Z}}) に基づくものとする。なお、　\tilde{\bm{Z}} = \sum_{l=1}^{L} \tilde{\bm{Z}}_l である。
ガウス分布の再生性より、新しい脱量子化過程は

     p_{s^2}(\tilde{\boldsymbol{z}}_i | \bm{Z}) = \mathcal{N} \left( \tilde{\boldsymbol{z}}_i ; \sum_{l=1}^{L} \boldsymbol{z}_{l,i}, \sum_{l=1}^{L} s_l^2 \bm{I} \right)
     
これを用いた新しい事前分布は

     \mathcal{P}(\bm{Z}_{1:L}, \tilde{\bm{Z}}) = \prod_{i=1}^{d_{\boldsymbol{z}}} \prod_{l=1}^{L} P(\bm{z}_{l,i}) p_{s^2}(\tilde{\bm{z}}_i | \bm{Z})
     
新しい事前・事後分布を用いたELBOベースの目的関数は、

  \begin{aligned}
  &\mathcal{J}_{\text{RSQ-VAE}}(\bm{x};\bm{\theta},\bm{\phi},\sigma^2,\bm{s}^{2},\mathcal{B}) \\
  &= \frac{D}{2}\log\sigma^2 + \mathbb{E}_{Q(\bm{Z}_{1:L},\tilde{\bm{Z}}_{1:L}|x)}\Biggl[\frac{\|\bm{x} - \bm{f}_{\bm{\theta}}(\bm{Z}_{1:L})\|_2^2}{2\sigma^2} + \frac{\|\tilde{\bm{Z}} - \bm{Z}\|_F^2}{2\sum_{l=1}^{L}s_l^2} - \sum_{l=1}^{L}H(\hat{P}_{s_l^2}({\bm{Z}}_l|\tilde{\bm{Z}}_l))\Biggr]
  \end{aligned}
  ここで \tilde{\bm{Z}} = \sum_{l=1}^{L}\tilde{\bm{Z}}_l であり、第3項では全体的な量子化誤差のみを評価する。この改良により、情報が上層に偏る問題を回避し、より安定した訓練が可能になる。
実験結果

RQ-VAEを上回る再構成精度を示し、上位層が活発に利用される。


 3.3 階層的離散表現の可視化
再構成画像を階層ごとに比較すると、上位層は大まかな構造、下位層はより微細な情報を担当している様子が見て取れる。
途中の階層までで打ち切って再構成と可視化を行うために、次に紹介する progressive coding の設定を追加している。

 4. 付録: progressive coding の概念論文では階層構造を用いて、漸進的に画像を高精細化する progressive coding （Ho et al., 2020; Shu & Ermon, 2022）のアイデアも提示されている。具体的には、各階層 l で

\tilde{\boldsymbol{x}}_{l} \sim \mathcal{N}\bigl(\tilde{\boldsymbol{x}}_{l};\, \boldsymbol{f}_{\bm{\theta}}(\bm{Z}_{1:l}),\, \sigma_l^{2}\boldsymbol{I}\bigr)
のような補助的な生成を行い、低次元情報のみで粗い再構成、上位層を追加するたびに精細化する仕組みを導入している。ELBOの導出までを丁寧に説明しよう。
階層 l \in [L] に対する破損データ \tilde{\bm{x}}_l を考える。これは入力データ \boldsymbol{x} にノイズを加えることで得られる。例えば、 \tilde{\bm{x}}_l = \bm{x} + \bm{\epsilon}_l とする。ここでは、ノイズにガウス分布 \bm{\epsilon}_{l,d} \sim \mathcal{N}(0, v_l) を採用する。なお、 \{\sigma_l^2\}_{l=1}^L は非増加列として設定されている。
上位 l 階層までを使用した生成過程をモデル化すると、

p_{\bm{\theta}}^l(\tilde{\bm{x}}_l) = \mathcal{N}(\tilde{\bm{x}}_l; \bm{f}_{\bm{\theta}}(\bm{Z}_{1:l}), \sigma_l^2 \boldsymbol{I})
progressive coding ではこの補助的な生成が全ての階層 l \in [L] で行われる。

たとえば、SQ-VAE-2のELBOベースの目的関数は次のようになる。

\begin{aligned}
&\mathcal{J}_{\textrm{SQ-VAE-2}}^{\textrm{prog}}(\boldsymbol{x}; \bm{\theta},\bm{\phi},\{\sigma_l^2\}_{l=1}^L,\{v_l\}_{l=1}^L, \bm{s}^{2},\mathcal{B}) \\
&= \sum_{l=1}^{L} \Bigg[\frac{D}{2}\log\sigma_l^2 + \mathbb{E}_{Q(\bm{Z}_{1:L},\tilde{\bm{Z}}_{1:L}|\bm{x})}\left[\frac{\|\bm{x} - \bm{f}_{\bm{\theta}}(\bm{Z}_{1:l})\|_2^2 + Dv_l}{2\sigma_l^2} + \frac{\|\tilde{\bm{Z}}_l - \bm{Z}_l\|_F^2}{2s_l^2} - H(\hat{P}_{s_l^2}({\bm{Z}}_l|\tilde{\bm{Z}}_l))\right]\Bigg]
\end{aligned}
ここで、

\boldsymbol{x}: 入力データ

\bm{\phi}: エンコーダのパラメータ

\bm{\theta}: デコーダのパラメータ

\{\sigma_l^2\}_{l=1}^L: 各階層での生成モデルの分散パラメータ

\{v_l\}_{l=1}^L: 破損データ生成時のノイズ分散パラメータ
3.3のSQ-VAE-2の段階的可視化ではこのテクニックが有効になっているが、上記の目的関数の引数のうち、破損データ生成のノイズ分散をシンプルにv_l = 0に固定している。

 まとめ
HQ-VAE は階層型VQ-VAE（VQ-VAE-2やRQ-VAE）を確率的量子化（SQ）で拡張し、コードブック崩壊を効果的に防ぎながら再構成性能を向上させる。

SQ-VAE-2（Injected型）と RSQ-VAE（Residual型）の2例が示され、どちらも従来手法を上回る性能とコードブック使用率を実現。

progressive coding により、漸進的な再構成が可能になり、生成モデルとしての柔軟性も拡がる。
以上、HQ-VAEの概要と主要な成果についての解説でした。階層的離散表現学習と確率的量子化の組み合わせが生み出す新たな可能性を、ぜひ論文本体でも確認してみてください。