[論文紹介＆検証] B-Learner

Paper

B-Learner: Quasi-Oracle Bounds on Heterogeneous Causal Effects Under
Hidden Confounding (記事のタイトルに入りきらなかった)
https://arxiv.org/pdf/2304.10577

論文内では推定誤差のorderなどの理論が多々現れますが、今回の論文紹介ではかなり省略します。興味のある方は論文も確認してみてください。

Introduction

Meta-Learner系の中では割と最近発表されたB-Learnerの論文について紹介します。
B-Learnerは、隠れた交絡因子のレベルを想定した上で、CATEの予測に加えてsharp boundを学習するものになります。（交絡因子のレベルはドメイン知識で補う必要があります。）

sharp boundとは観察データと隠れた交絡因子の影響(ドメイン知識)を考慮に入れた最小限の境界です。これよりも緩めの境界はvalid boundと呼ばれ、真の因果効果に加えて余分な値も含む境界のことです。つまり、valid boundを用いて意思決定を行う場合は慎重にする必要があります。

Background and setup

今回は、Neyman-Rubinのoutcomeフレームワークを用います。データ$(X, A, Y(1), Y(0), U)$は、観測不能な分布$P_{\text{full}}$から抽出されたものとし、処置は$A \in \{0, 1\}$、共変量は$X \in \mathbb{R}^{d}$、$Y(0),Y(1)$は処置を受けていない場合、受けた場合の潜在的なoutcome、観測不能な交絡因子は$U \in \mathbb{R}^{k}$で表されます。

この前提の元、CATE（Conditional Average Treatment Effect）は、outcomeの差で求めることができます。

$$\tau(x) = \mathbb{E}_{P_{\text{full}}}[Y(1) - Y(0) \mid X = x].$$

また、交絡因子が存在しない場合は、CATEは潜在outcomeの期待値の差で導出できます。

$$\tau(x) = \mathbb{E}_{P}[Y \mid X = x, A = 1] - \mathbb{E}_{P}[Y \mid X = x, A = 0]$$

しかし、観測された共変量$X$だけでは説明できない交絡はある程度存在します。そこで、未観測の交絡によって$P_{\text{full}}$と$P$が乖離する範囲を周辺感度モデルを用いて考えます。$P_{\text{full}}$と$P$から得られる傾向スコアを $e(x, u) = P_{\text{full}}(A = 1 \mid X = x, U = u) , e(x) = P(A = 1 \mid X = x)$ として、処置オッズ比を感度パラメーターで挟み込みます。

$$\Lambda^{-1} \leq \frac{e(x, u)}{1 - e(x, u)} \bigg/ \frac{e(x)}{1 - e(x)} \leq \Lambda.$$

$\Lambda=1$のとき、未観測の交絡因子の影響は無いと考えられ、$\Lambda$が1から離れると、CATEの境界が推定されることになります。B-Leanerは、この境界を特徴づけることが目的です。

感度パラメータ$\Lambda$は、どれだけの交絡を許容するかのハイパーパラメータです。$\Lambda$が増加すると区間が広がるので、意思決定が覆される$\Lambda$がないかを判断していく必要があります。

Properties of bound estimates

未観測の交絡を含むデータ$(X, A, Y(1), Y(0), U)$の集合を$Q$とし、$e^{*}$を観測データから得られた傾向スコアとすると、$Q$を用いて先ほどの定義式を書き換えられます。

$$\Lambda^{-1} \leq \frac{Q(A=1 \mid X=x, U=u)}{Q(A=0 \mid X=x, U=u)} \bigg/ \frac{e^{*}(x)}{1 - e^{*}(x)} \leq \Lambda$$

集合$Q$の条件付き集合を$\Lambda$で挟み込んだ状況で、outcomeとCATEの上限を定義します。この形式であれば、CATEの上限$\tau^{+}(x)$は、観測データと感度パラメータのみに依存することになります。

$$\begin{aligned} Y^{+}(x, a) &\equiv \sup_{Q \in \mathcal{M}(\Lambda)} \mathbb{E}_{Q}[Y(a) \mid X = x]\\ \tau^{+}(x) &\equiv \sup_{Q \in \mathcal{M}(\Lambda)} \mathbb{E}_{Q}[Y(1) - Y(0) \mid X = x] \end{aligned}$$

下限はsupをinfに変換すれば得られます。$+$は上限、$-$は下限を示します。

Valid estimates

$\bar{\tau}^{+}(x) \geq \tau^{+}(x)$をvalid estimatesと呼びます。ただし、今回はやや緩和して$\hat{\tau}^{+}(x) \geq \tau^{+}(x) - o_{p}(1)$にしています。
逆に、$\hat{\tau}^{+}(x) < \tau^{+}(x) - o_{p}(1)$ は、真の介入効果を含まない形なので、望ましくない結果となります。

Sharp estimates

$\hat{\tau}^{+}(x) = \tau^{+}(x) + o_{p}(1)$をsharp estimatesと呼びます。sharp estimatesはvalid estimatesよりも強い特性になります。

bound estimates example

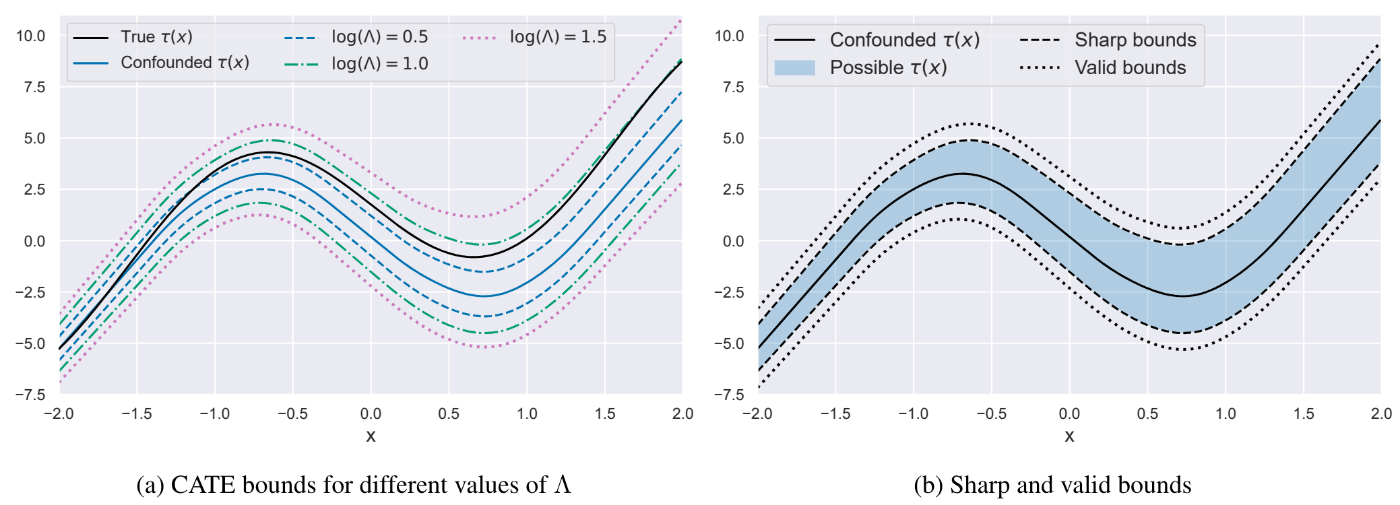
図1. 真のオッズ比$\Lambda^*$によって与えられる交絡されたCATEの例。(1a) : 異なるレベルの$\Lambda$に対するsharp boundを示したもの (1b) : valid、sharp CATE boundの例
$\log(\Lambda^*) = 1.0$の範囲であれば、真の介入効果を含めることができています。これ以上広げると余分な境界になっていきそうです。

Identification and estimation of sharp bounds

観測データ分布$P$によって、CATEのsharp boundを形式化します。
まずは、CVaR（Conditional Value at Risk）と未観測のoutcome境界に対応するような、擬似outcomeを導入します。$H$がCVaR、$R$が未観測のoutcome境界、$\rho_{\pm}^{\ast}$はsharp boundに対応します。

$$\begin{aligned} H_{\pm}(z, q) &= q(x, \alpha) + \frac{1}{1 - \alpha} [y - q(x, \alpha)]_{\pm} \\R_{\pm}(z, q) &= \Lambda^{-1} y + (1 - \Lambda^{-1}) H_{\pm}(z, q) \\\rho_{\pm}^{*}(x, q) &= E[R_{\pm}(z, q) | X = x, A = a] \end{aligned}$$

施策の効果が全体（ATE）ではプラスであったとしても、個々の効果(ITE)では、マイナスの可能性があります。このマイナス影響をリスクと捉え、形式化したものがCVaRです。
https://arxiv.org/pdf/2201.05893

$Q$と$P$が一致する場合、条件付き潜在outcome $Y$は、観測データの条件付きoutcomeは$\mu^{*}(x, a) = \mathbb{E}[Y \mid X = x, A = a]$を用いて表現できます。

$$\begin{aligned} \mathbb{E}_{Q}[Y(a) \mid X = x] = P[A &= a \mid X = x]×\mu^{*}(x, a) \\ &+ P[A = 1 - a \mid X = x] ×\mathbb{E}_{Q}[Y(1 - a) \mid X = x, A = a] \end{aligned}$$

ここで、sharp bound $\rho_{\pm}^{\ast}$を用いれば、$\mathbb{E}_{Q}[Y(1 - a) \mid X = x, A = a]$のsharp boundの上下限を表せます。

$$Y^{+}(x, 1) = e^{\ast}(x) \mu^{\ast}(x, 1) + (1 - e^{\ast}(x)) \rho^{\ast}_{+}(x, 1) \\ Y^{-}(x, 0) = (1 - e^{\ast}(x)) \mu^{\ast}(x, 0) + e^{\ast}(x) \rho^{\ast}_{-}(x, 0)$$

以上より、CATEのsharp boundの上限は $\tau^{+}(x) = Y^{+}(x, 1) - Y^{-}(x, 0)$と表すことができるようになりました。また、sharp boundの上限は、$P$から推定可能な条件付きoutcomeとCVaRの凸結合で表現できました。

ただし、反実仮想$\mathbb{E}_{Q}[Y(1 - a) \mid X = x, A = a]$をうまく特徴づける必要があります。

$\tau^{+}$によってvalid / sharp boundが得られました。しかし、感度パラメータがハイパーパラメータであること、真の$q$は確認できないことなどから、まだ準オラクル推定には不十分とも言えます。

（ここまでが導入です。）

（本編）B-Learner: Pseudo-Outcome Regression for Doubly-Robust Sharp CATE Bounds

先ほどまででCATEのsharp boundを形式化してきました。ここからは、さらにsharp boundの精度を上げる工夫を施し、B-Learnerを提案する章になります。

Pseudo-outcome regression for quasi-oracle estimation

$\tau^{+}$内の$e,\mu,\rho$を観測データから推定するようなプラグイン推定では、過度のバイアスが入ります。そこで、影響関数に基づいてvalid boundの疑似outcomeを導出し、それを共変量$X$に回帰させることで、先の結果よりも望ましい特性を持つsharp boundのCATEを推定します。

影響関数は、条件付きDTE（CDTE）を学習するために使われた関数系で、doubly-robustと似たような形になっています。https://arxiv.org/pdf/2205.11486 ↓こんな感じ

$$\begin{aligned} \psi(Z, e, \alpha, \nu) = \kappa_1(X) - \kappa_0(X) - \frac{A - e(X)}{e(X)(1 - e(X))} \alpha_A(X)^T \rho(Y, \nu_A(X)). \end{aligned}$$

推定されたnuisanceを $\hat{\eta} = (\hat{e}, \hat{q}_{-}(\cdot, 0), \hat{q}_{+}(\cdot, 1), \hat{\rho}_{-}(\cdot, 0), \hat{\rho}_{+}(\cdot, 1)) \in \Xi$ とし、$Y^{+}(x, 1), Y^{-}(x, 0), \tau^{+}(x)$に対応する疑似outcomeを定義します。

$$\begin{aligned} \phi_{1}^{+}(Z, \hat{\eta}) &= AY + (1 - A) \hat{\rho}_{+}(X, 1)\\ &+ \frac{(1 - \hat{e}(X)) A}{\hat{e}(X)} \cdot (R_{+}(Z, \hat{q}_{+}(X, 1)) - \hat{\rho}_{+}(X, 1)),\\ \\ \phi_{0}^{-}(Z, \hat{\eta}) &= (1 - A)Y + A \hat{\rho}_{-}(X, 0)\\ & + \frac{\hat{e}(X) (1 - A)}{1 - \hat{e}(X)} \cdot (R_{-}(Z, \hat{q}_{-}(X, 0)) - \hat{\rho}_{-}(X, 0)),\\ \\ \phi_{\tau}^{+}(Z, \hat{\eta}) &= \phi_{1}^{+}(Z, \hat{\eta}) - \phi_{0}^{-}(Z, \hat{\eta}). \end{aligned}$$

$\phi_{1}^{+}(Z, \hat{\eta})$の右辺第３項目は$\hat{\rho}_{+}$の予測誤差を直行化する役割になります。これによって、擬似outcomeの境界を定式化できました。

擬似outcomeは、観測データ分布$P$にのみ依存するため、観測データの統計推定量と見做すことができます。特に、$A=1$かつ交絡がない場合、$\phi_{\tau}^{+}(Z, \hat{\eta})$はdoubly-robustの疑似outcomeと似たような形になります。

Algorithm

B-Learnerは2段階の推定手法になっています。
第1段階では、k-foldのクロスフィッティングでnuisances（outcome、傾向スコア、CVaR）を推定し、擬似outcome推定量を構築します。第2段階では、推定された擬似outcomeを共変量$X$で回帰し、CATE boundを得ます。

傾向スコア$e^{*}(x)$や分位数$q_{\pm}^{*}$は標準的な分類器や回帰モデルで導出します。

また、outcome $\rho_{\pm}^{*}(x, a) = \Lambda^{-1}\mu^{*}(x, a) + (1 - \Lambda)^{-1}CVaR_{\pm}(x, a)$の導出は、$\mu^{*}(x, a)$と$CVaR_{\pm}(x, a)$ を別々に予測することなどによって可能です。

第一段階だけでは、sharp bound バイアスの推定誤差は$|\hat{e} - e^*| |\hat{\rho} - \rho^*| + (\hat{q} - q^*)^2$になります。第二段階まで行うことで、ロバストな推定ができるようです。
また、四分位推定に一貫性がない場合は、$(\hat{q}_+- q_+^*)^2 , (\hat{q}_- - q_-^*)^2$が打ち消せなくなります。その場合はsmoothing estimationを使うことで対応するようです。
https://arxiv.org/pdf/2004.14497

Experiments

論文中ではシミュレーションデータ、IHDP、401(k) Eligibilityの3種で検証を行っていました。今回は401(k) Eligibilityの結果のみ記載します。

Impact of 401(k) Eligibility on Wealth Distribution

401(k) Eligibilityは、401(k)資格とその金融資産への影響に関するデータセットです。このデータセットは交絡がないことがわかっていますが、交絡があると仮定して$\Lambda$を変化させてB-Learnerの検証をします。

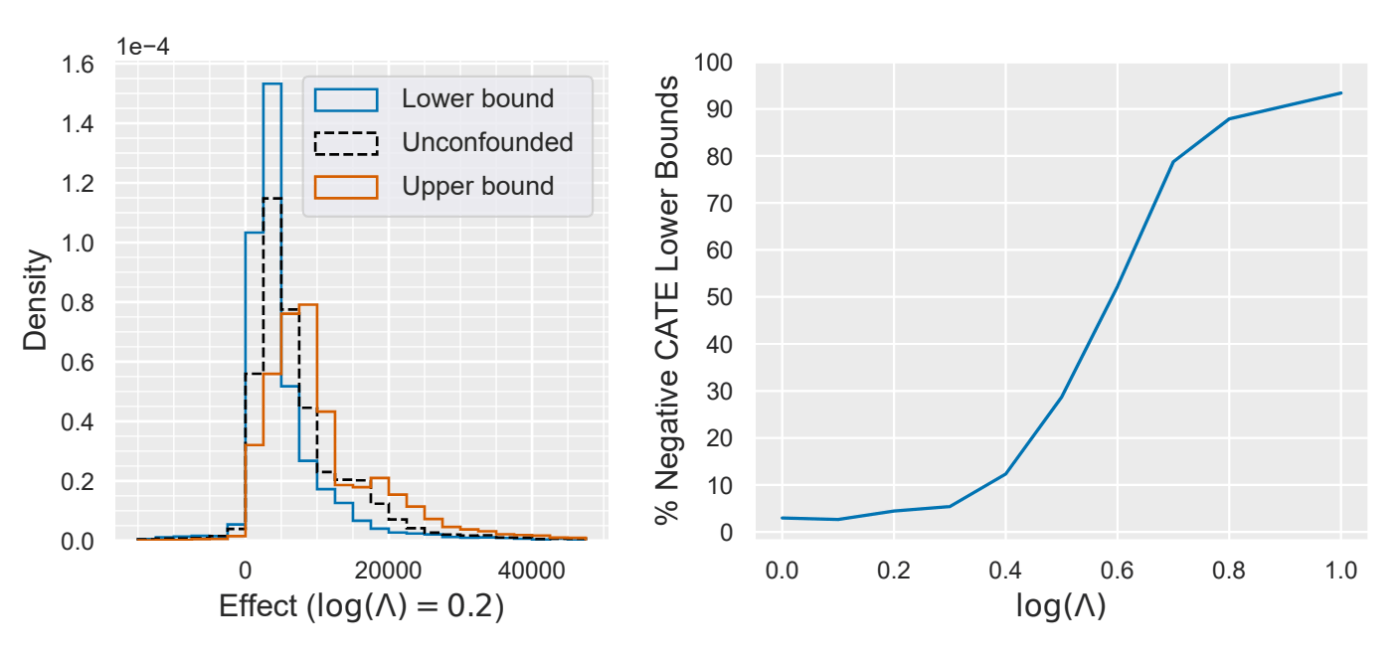
左図：$log\Lambda=0.2$では、lower boundとupper boundの間に真の効果が含まれています。
右図：$log\Lambda$を変化させたときに、介入効果が$\hat{\tau(x)}<0$になった割合を示しています。$\Lambda$が小さい時は、多くが正になっていますが、$log\Lambda=0.6$程度まで増えると半分程度が負になってしまいます。つまり、 このレベルの影響を出す交絡因子が隠れていた場合、半分程度は未観測の購買率によって負の影響を出していた可能性があります。 B-Learnerによって、こういったリスクを定量化することができました。

検証

B-Learnerは著者がgitにコードを提供してくれているので検証してみます。
今回は、論文中に評価が行われていたシミュレーションデータを用いて、lower upper boundが推定できていることを確かめようと思います。
シミュレーションのデータ生成過程は以下の形式です。($\sigma$はシグモイド関数です。)

$$\begin{aligned} X &\sim \text{Unif}([-2, 2]^5) \\ A \mid X &\sim \text{Bern}(\sigma(0.75X_0 + 0.5)) \\ Y &\sim \mathcal{N}((2A - 1)(X_0 + 1) - 2\sin((4A - 2)X_0), 1) \\ \end{aligned}$$

git cloneでコードを引っ張ってきます。

!git clone https://github.com/CausalML/BLearner.git
cd BLearner

中には著者が準備してくれているgeneratorがあるので、それをそのまま使います。

from datasets import synthetic #データ生成器
generator = synthetic.Synthetic(num_examples=10000, gamma_star=1, mode='mu')

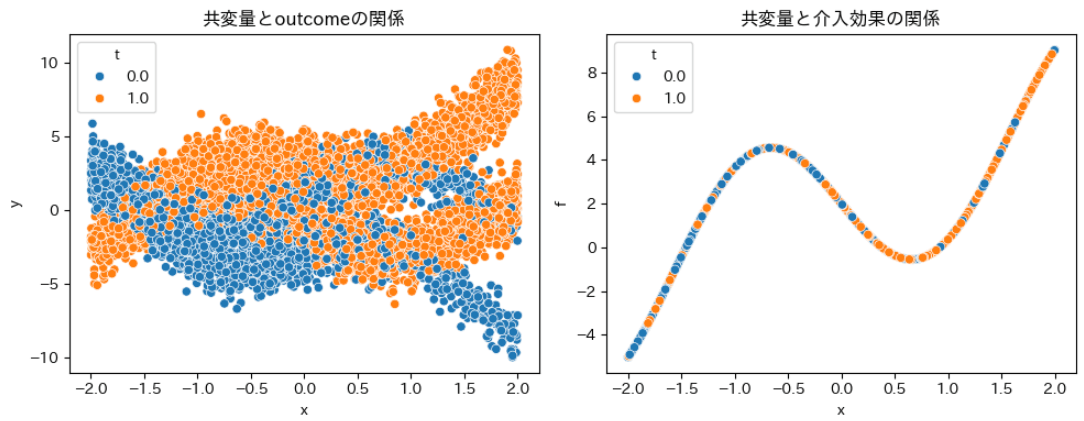
データを取り出してみるとこんな感じでした。共変量に対して介入効果が非線形に与えられているのが分かります。

print(f'ATE:{generator.tau_fn(generator.x).mean()}')
ATE:2.021308422088623

ATEも見ておきます。おおよそ2くらいの介入効果でした。

次にB-Learnerの推定器を作ります。まずは、各コンポーネントの回帰・分類モデルを定義しておきます

gamma = np.e # log(gamma) = 1 の場合
tau = gamma / (1+gamma)

#傾向スコアモデル
propensity_model = lightgbm.LGBMClassifier()

#outcomeモデル
mu_model = lightgbm.LGBMRegressor()

#四分位予測モデル
quantile_model_upper = RandomForestQuantileRegressor(q=tau)
quantile_model_lower = RandomForestQuantileRegressor(q=1-tau)

#CVaR上界モデル
cvar_model_upper = KernelSuperquantileRegressor(kernel=RFKernel(clone(mu_model, safe=False)),
                                                tau=tau, tail="right")
#CVaR下界モデル
cvar_model_lower = KernelSuperquantileRegressor(kernel=RFKernel(clone(mu_model, safe=False)),
                                                tau=1-tau, tail="left")

# CATE境界モデル
cate_bounds_model = lightgbm.LGBMRegressor()

これらを全て入れ込むとB-Leanerの推定器が作れます。

estimator = BLearner(propensity_model = propensity_model,
                     mu_model = mu_model,
                     quantile_plus_model  = quantile_model_upper,
                     quantile_minus_model = quantile_model_lower,
                     cvar_plus_model   = cvar_model_upper,
                     cvar_minus_model  = cvar_model_lower,
                     cate_bounds_model = cate_bounds_model,
                     use_rho=True,
                     gamma=gamma)

引数が大量にあって、かなりややこしいですが、、、一応論文で説明されたモデルがすべて入っていることが分かります。

print(f'estimated ATE:{estimator.mu1(X) - estimator.mu0(X)}')
estimated ATE:2.0081604922300373

実際に推定してみるとATEが2程度になり、ちゃんと推定できていることがわかります。

print(f'estimated lower:{effects[0].mean()}')
estimated lower:-0.46066781397843126

print(f'estimated upper:{effects[1].mean()}')
estimated upper:4.610615861659414

上下限も見てみました。率直な感想は思ったより広かったです、、、がこんなもんなのかもしれません。

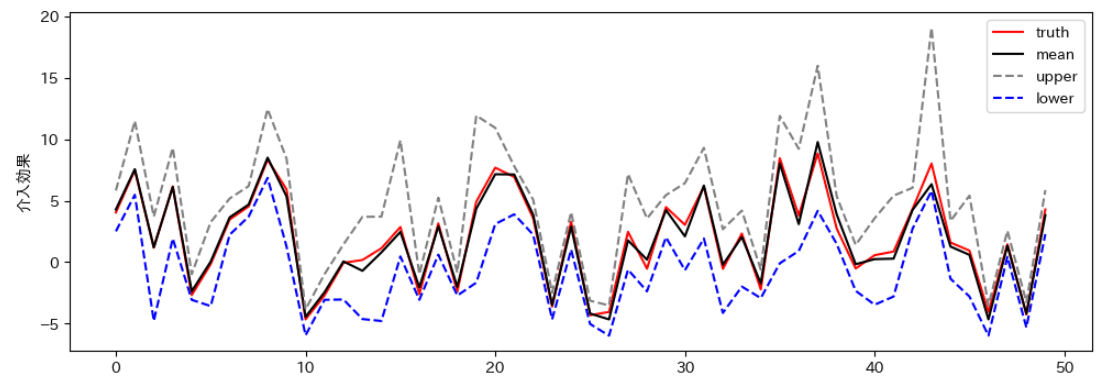
ITEの上下限もプロットしてみました。ほぼすべての点で、きれいに上下限を表せていました。

次に感度パラメータを変更してみます。

gamma = np.e ** 3

print(f'estimated ATE:{estimator.mu1(X) - estimator.mu0(X)}')
estimated ATE:2.01403225907998

print(f'estimated lower:{effects[0].mean()}')
estimated lower:-5.598983732440596

print(f'estimated upper:{effects[1].mean()}')
estimated upper:10.217975521577744

ATEは変わらず、上下限がかなり広がったことが分かります。未観測の交絡因子の大きさがどの程度あるかをシミュレーションする分には楽しめそうですね！

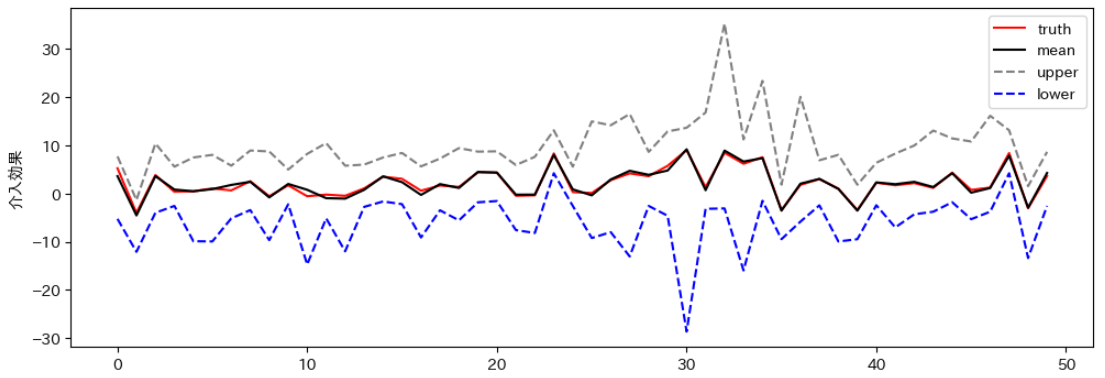
ITEのプロットも見てみると、こちらも先ほどよりも幅が広がってることがわかります。

まとめ

今回はMeta-Learner系の中では割と最近発表されたB-Learnerの論文について紹介しました。これまでのMeta-Learnerの機能を持ち合わせつつ、感度パラメータによって未観測の交絡因子の影響を可視化できるようになりました。しかし、感度パラメータの取り扱いはかなり難しい（事業的なお気持ちも入る）ので、どのくらいの影響までを許容するのかを相手方とうまくすり合わせる必要があります。この推定器でシミュレーションした結果は、そのコミュニケーションツールの一つになるかもしれないとも思いました。