Zenn
DMM Data BlogPublicationへの投稿
💨

Pythonで再現する標準ベイズ統計学9章

stochi
2024/09/11に公開
データ分析
統計学
データサイエンティスト
回帰分析
ベイズ統計学
tech

はじめに

本記事では標準ベイズ統計学の9章で掲載されている図表やモデルをPythonで実装する方法に関して説明します。

9章：線形回帰

標準ベイズ統計学の9章では主にベイズ線形回帰モデル・ベイズ的な変数選択について解説が行われています。最大酸素摂取量データを使った分析から始まり、g事前分布を用いたベイジアン推定を行います。次に、糖尿病データセットを用いて、通常の最小二乗法（OLS）、変数選択法、そしてベイジアンモデル平均化（BMA）を比較検討しています。

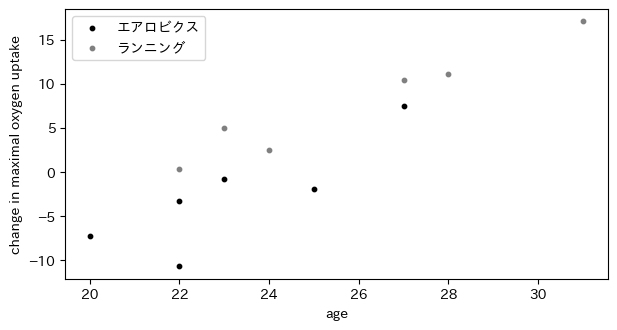
最大酸素摂取量の変化を年齢と運動療法の種類の関数として描いたもの

図9.1は最大酸素摂取量の変化を年齢と運動療法の種類の関数として描いたものです。横軸を年齢、縦軸を最大酸素摂取量の変化としています。また、灰色の点がエアロビクス、黒点がランニングを示しています。

import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np

# データの設定
x1 = np.array([0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1])
x2 = np.array([23, 22, 22, 25, 27, 20, 31, 23, 27, 28, 22, 24])
y = np.array([-0.87, -10.74, -3.27, -1.97, 7.50, -7.25, 17.05, 4.96, 10.40, 11.05, 0.26, 2.51])

# 散布図の作成
plt.figure(figsize=(7, 3.5))
plt.scatter(x2[x1 == 0], y[x1 == 0], c='black', label='エアロビクス', s=10)
plt.scatter(x2[x1 == 1], y[x1 == 1], c='gray', label='ランニング', s=10)
plt.xlabel('age')
plt.ylabel('change in maximal oxygen uptake')
plt.legend()

plt.show()
plt.close()

酸素摂取量データに対する四つのモデルの最小二乗推定量に基づく回帰直線

図9.2では酸素摂取量データに対する4つのモデルの最小二乗推定量に基づく回帰直線をプロットしています。
回帰式は以下のとおりです。

Y_i = \beta_1 x_{i,1} + \beta_2 x_{i,2} + \beta_3 x_{i,3} + \beta_4 x_{i,4} + \epsilon_{i}
x_{i,1} = 1 (すべての被験者iで共通)
x_{i,2} = 0 (被験者iがランニングを行う場合) \\ = 1 (エアロビクスの場合)　\\
x_{i,3} = 被験者iの年齢
x_{i,4} = x_{i,2} × x_{i,3} 
import statsmodels.api as sm

# 図の作成
plt.figure(figsize=(6, 5.5))

# サブプロット1
plt.subplot(2, 2, 1)
plt.scatter(x2, y, c=['black' if i == 0 else 'gray' for i in x1], label='aerobic', s=10)
plt.axhline(y=y[x1==0].mean(), color='black')
plt.axhline(y=y[x1==1].mean(), color='gray')
plt.ylabel('change in maximal oxygen uptake')
plt.xticks([])
plt.title(r'$\beta_3=0\ \beta_4=0$')

# サブプロット2
plt.subplot(2, 2, 2)
plt.scatter(x2, y, c=['black' if i == 0 else 'gray' for i in x1], label='running', s=10)
plt.plot(np.unique(x2), np.poly1d(np.polyfit(x2, y, 1))(np.unique(x2)), color='black')
plt.plot(np.unique(x2), np.poly1d(np.polyfit(x2, y + 0.5, 1))(np.unique(x2)), color='gray')
plt.xticks([])
plt.yticks([])
plt.title(r'$\beta_2=0\ \beta_4=0$')

# サブプロット3
plt.subplot(2, 2, 3)
plt.scatter(x2, y, c=['black' if i == 0 else 'gray' for i in x1], s=10)
fit = sm.OLS(y, sm.add_constant(np.column_stack((x1, x2)))).fit()
b0, b1, b2 = fit.params
plt.plot(x2, b0 + b2*x2, color='black')
plt.plot(x2, (b0 + b1) + b2*x2, color='gray')
plt.xlabel('age')
plt.ylabel('change in maximal oxygen uptake')
plt.title(r'$\beta_4=0$')

# サブプロット4
plt.subplot(2, 2, 4)
plt.scatter(x2, y, c=['black' if i == 0 else 'gray' for i in x1], s=10)
fit0 = sm.OLS(y[x1==0], sm.add_constant(x2[x1==0])).fit()
fit1 = sm.OLS(y[x1==1], sm.add_constant(x2[x1==1])).fit()
plt.plot(x2, fit0.predict(sm.add_constant(x2)), color='black')
plt.plot(x2, fit1.predict(sm.add_constant(x2)), color='gray')
plt.xlabel('age')
plt.yticks([])

plt.tight_layout()
plt.show()

\beta_2と\beta_4の事後分布

g事前分布を回帰パラメータの事前分布として利用し、以下のようにして\sigma^2と\betaをサンプリングを行い、\beta_2と\beta_4と両者の相関を表したプロットが図9.3です。ここではg=n=12、\nu_0 = 1、\sigma^2_{0}=\hat{\sigma}^2_{ols} = 8.54としています。

\frac{1}{\sigma^2} \sim gamma([\nu_0 + n]/2, [\nu_0\sigma^2_0 + SSR_{g}]/2) \\ SSR_{g} = y^{T}(I - \frac{g}{g+1}X(X^{T}X)^{-1}X^{T})y
\beta \sim multivariate\ normal(\frac{g}{g+1}\hat{\beta}_{ols}, \frac{g}{g+1}\sigma^2[X^{T}X]^{-1}) 
import scipy.stats as stats
import scipy.linalg as linalg
from scipy.stats import gaussian_kde
from scipy.stats import t, gamma
from scipy.special import gamma

# データの設定
n = len(y)
X = np.column_stack((np.ones(n), x1, x2, x1 * x2))
p = X.shape[1]
# すでに定義している
# y = np.array([-0.87, -10.74, -3.27, -1.97, 7.50, -7.25, 17.05, 4.96, 10.40, 11.05, 0.26, 2.51])

def lm_gprior(y, X, g=None, nu0=1, s20=None, S=1000):
    np.random.seed(100)
    n, p = X.shape
    if g is None:
        g = p
    if s20 is None:
        s20 = np.var(y, ddof=1)

    Hg = (g / (g + 1)) * X @ linalg.inv(X.T @ X) @ X.T
    SSRg = y.T @ (np.eye(n) - Hg) @ y

    s2 = 1 / stats.gamma.rvs((nu0 + n) / 2, scale=2 / (nu0 * s20 + SSRg), size=S)

    Vb = g * linalg.inv(X.T @ X) / (g + 1)
    Eb = Vb @ X.T @ y

    E = np.array([np.random.normal(0, np.sqrt(s2[i]), p) for i in range(S)])
    beta = np.array([E[i] @ np.linalg.cholesky(Vb).T + Eb for i in range(S)])

    return {'beta': beta, 's2': s2}

# g-事前分布を用いたベイジアン推定
tmp = lm_gprior(y, X, g=12)
beta_post = tmp['beta']

# OLS推定
beta_ols = np.linalg.lstsq(X, y, rcond=None)[0]

g = n
nu0 = 1
s20 = np.var(y - X @ beta_ols, ddof=X.shape[1])
beta_ols_g = beta_ols * g / (g + 1)
iXX = np.linalg.inv(X.T @ X)

# t分布の密度関数
def mdt(t, mu, sig, nu):
    return stats.t.pdf(t, df=nu, loc=mu, scale=sig)

# サブプロット1
plt.figure(figsize=(10, 3), dpi=100)
x = np.linspace(-85, 130, 200)
kde = gaussian_kde(beta_post[:, 1])
plt.subplot(1, 3, 1)
plt.plot(x, kde(x), lw=2)
plt.axvline(x=0, color="gray")
plt.plot(x, mdt(x, 0, np.sqrt(n * s20 * iXX[1, 1]), nu0), color="gray")
plt.xlabel(r'$\beta_2$')
plt.title("")

# サブプロット2
x = np.linspace(-5, 5, 100)
kde = gaussian_kde(beta_post[:, 3])
plt.subplot(1, 3, 2)
plt.plot(x, kde(x), lw=2)
plt.axvline(x=0, color="gray")
plt.plot(x, mdt(x, 0, np.sqrt(n * s20 * iXX[3, 3]), nu0), color="gray")
plt.xlabel(r'$\beta_4$')
plt.title("")

# サブプロット3: KDEと等高線を使用
beta2_beta4 = beta_post[:, [1, 3]]
kde = gaussian_kde(beta2_beta4.T)
plt.subplot(1, 3, 3)
xgrid, ygrid = np.meshgrid(np.linspace(beta2_beta4[:, 0].min(), beta2_beta4[:, 0].max(), 100),
                           np.linspace(beta2_beta4[:, 1].min(), beta2_beta4[:, 1].max(), 100))
z = kde(np.vstack([xgrid.ravel(), ygrid.ravel()]))
plt.contour(xgrid, ygrid, z.reshape(xgrid.shape))
plt.axhline(y=0, color="gray")
plt.axvline(x=0, color="gray")
plt.xlabel(r'$\beta_2$')
plt.ylabel(r'$\beta_4$')

plt.tight_layout()
plt.show()

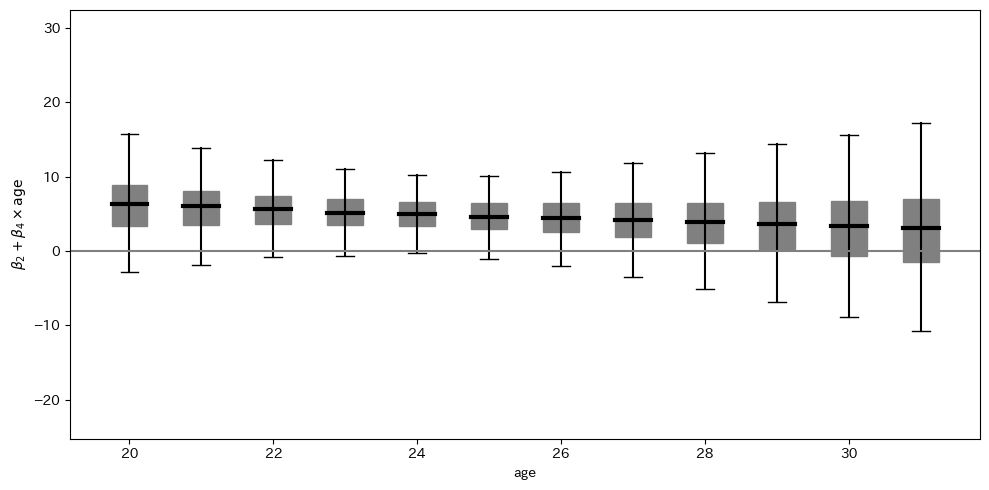
エアロビクスとランニングのグループ間の変化量のの期待値の差の95%信用区間

図9.4では、ランニングと比較した際のエアロビクスの効果を示しています。この効果は、各年齢xに対して\beta_2 + \beta_4xの形で表される事後分布として得られます。図中では、この事後分布を年齢ごとに箱ひげ図でプロットしています。この図より年齢が低いと、エクササイズを行った二つのグループ間のyに差があることがわかります。

# ベイジアン回帰線の事後分布の計算
BX = np.array([beta_post[s, 1] + np.arange(min(X[:, 2]), max(X[:, 2]) + 1) * beta_post[s, 3] for s in range(beta_post.shape[0])])

# プロット用の関数
def qboxplot(x, at=0, width=0.5, probs=[0.025, 0.25, 0.5, 0.75, 0.975]):
    qx = np.quantile(x, probs)
    plt.plot([at, at], [qx[0], qx[4]], color='black')  # 線
    plt.fill([at - width, at + width, at + width, at - width], [qx[1], qx[1], qx[3], qx[3]], color='gray')  # 箱
    plt.plot([at - width, at + width], [qx[2], qx[2]], color='black', lw=3)  # 中央値
    plt.plot([at - width / 2, at + width / 2], [qx[0], qx[0]], color='black', lw=1)  # 上下ヒゲ
    plt.plot([at - width / 2, at + width / 2], [qx[4], qx[4]], color='black', lw=1)

# 図の作成
plt.figure(figsize=(10, 5))
plt.xlabel('age')
plt.ylabel(r'$\beta_2 + \beta_4 \times \mathrm{age}$')
plt.ylim(np.min(BX), np.max(BX))

for age in range(BX.shape[1]):
    qboxplot(BX[:, age], at=age + 20, width=0.25)

plt.axhline(y=0, color='gray')

plt.tight_layout()
plt.show()

糖尿病データにおける予測値と回帰係数

糖尿病患者のデータをトレーニングデータとテストデータに分割し、トレーニングデータに対して64個の説明変数を持つ回帰モデルを適用します。その後、推定された回帰係数\hat{\beta}を使用して、\hat{y}_{test} = X_{test}\hat{\beta}によりテストデータの予測値を計算します。この \hat{y}_{test}を縦軸に、y_{test}を横軸に取ったグラフが図9.5の左図です。中央の図には、64個の回帰係数の推定値が表示されています。右の図では、変数減少法を用いて変数を削減した後の回帰モデルを適用し、その推定された回帰係数を使って計算された\hat{y}_{test}を縦軸に、y_{test}を横軸に取ったグラフが示されています。

from scipy.stats import norm
import pandas as pd

# 後方選択関数
def bselect(y, X, tcrit=1.65):
    Xc = X.copy()
    remain = list(range(Xc.shape[1]))
    removed = []

    while remain:
        fit = sm.OLS(y, Xc).fit()
        t_stats = fit.tvalues
        
        if all(abs(t_stats) >= tcrit):
            break

        jmin = np.argmin(abs(t_stats))
        Xc = np.delete(Xc, jmin, axis=1)
        removed.append(remain.pop(jmin))

    return {'remain': remain, 'removed': removed}

# データの読み込み
diabetes_df = pd.read_csv('./diabetes.csv')

# 目的変数（yf）と説明変数（Xf）の設定
yf = diabetes_df['y']
yf = (yf - yf.mean()) / yf.std()

Xf = diabetes_df.drop('y', axis=1)
Xf = (Xf - Xf.mean()) / Xf.std()

# トレーニングデータとテストデータの設定
n = len(yf)
np.random.seed(10)
i_te = np.random.choice(range(n), 100, replace=False)
i_tr = np.array([i for i in range(n) if i not in i_te])

y = yf.iloc[i_tr]
y_te = yf.iloc[i_te]
X = Xf.iloc[i_tr]
X_te = Xf.iloc[i_te]

# OLSモデルのフィット
ols_model = sm.OLS(y, X).fit()
y_te_ols = ols_model.predict(X_te)

# 後方選択を使ってモデルをフィット
bsl_indices = bselect(y, X, tcrit=1.65)['remain']
X_bsl = X.iloc[:, bsl_indices]
X_te_bsl = X_te.iloc[:, bsl_indices]
bsl_model = sm.OLS(y, X_bsl).fit()
y_te_bsl = bsl_model.predict(X_te_bsl)

# プロット1: テストデータの予測値 vs 実際の値
plt.figure(figsize=(10, 4))
plt.subplot(1, 3, 1)
plt.scatter(y_te, y_te_ols)
plt.plot([y_te.min(), y_te.max()], [y_te.min(), y_te.max()], 'r--')
plt.xlabel(r'$y_{\mathrm{test}}$')
plt.ylabel(r'$\hat{y}_{\mathrm{test}}$')
plt.title('OLS Prediction')

# プロット2: OLS回帰係数
plt.subplot(1, 3, 2)
plt.bar(range(len(ols_model.params)), ols_model.params, color='b', alpha=0.7)
plt.xlabel('Regressor Index')
plt.ylabel(r'$\hat{\beta}_{\mathrm{OLS}}$')
plt.title('OLS Coefficients')

# 10の倍数のインデックスのみ目盛りとして設定
plt.xticks(ticks=[i for i in range(len(ols_model.params)) if i % 10 == 0])

# プロット3: 後方選択モデルのテストデータの予測値 vs 実際の値
plt.subplot(1, 3, 3)
plt.scatter(y_te, y_te_bsl)
plt.plot([y_te.min(), y_te.max()], [y_te.min(), y_te.max()], 'r--')
plt.xlabel(r'$y_{\mathrm{test}}$')
plt.ylabel(r'$\hat{y}_{\mathrm{test}}$')
plt.title('Backward Selection Prediction')

plt.tight_layout()
plt.show()

以下では通常のOLSと変数減少法後のOLSのMSEを計算しています。以下の結果を見るとわかるように、変数減少後の方がMSEが小さいため、予測がうまくいっていることがわかります。

# OLSモデルのMSE
mse_ols = np.mean((y_te - y_te_ols) ** 2)

# 後方選択モデルのMSE
mse_bsl = np.mean((y_te - y_te_bsl) ** 2)

# OLSモデルと後方選択モデルのMSEの出力
print(f"MSE OLS: {mse_ols}, MSE BSL: {mse_bsl}")
# MSE OLS: 0.6534133564607578, MSE BSL: 0.6279912317536374

変数減少の前と後で\tilde{y}をXに回帰したときのt統計量

# 図9.6のプロット
plt.figure(figsize=(10, 4))

# オリジナルデータのt統計量
ols_model = sm.OLS(y, X).fit()
t_stats = ols_model.tvalues

plt.subplot(1, 2, 1)
plt.bar(range(len(t_stats)), t_stats, color='b', alpha=0.7)
plt.axhline(y=0, color='black', linestyle='--')  # 横軸が0の位置に黒い点線を追加
plt.xlabel('Regressor Index')
plt.ylabel('t-statistic')
plt.title('Original Data')
plt.ylim(-4.8, 4.8)

# ランダムに並べ替えたデータのt統計量
y_perm = np.random.permutation(y)
ols_model_perm = sm.OLS(y_perm, X).fit()
t_stats_perm = ols_model_perm.tvalues

bsl_indices = bselect(y_perm, X, tcrit=1.65)['remain']
X_bsl = X.iloc[:, bsl_indices]
bsl_model = sm.OLS(y_perm, X_bsl).fit()

t_stats_bsl = np.zeros_like(t_stats_perm)
t_stats_bsl[bsl_indices] = bsl_model.tvalues

plt.subplot(1, 2, 2)
plt.bar(range(len(t_stats_bsl)), t_stats_bsl, color='b', alpha=0.7)
plt.axhline(y=0, color='black', linestyle='--')  # 横軸が0の位置に黒い点線を追加
plt.xlabel('Regressor Index')
plt.ylabel('t-statistic')
plt.title('Permuted Data (After Backward Selection)')
plt.ylim(-4.8, 4.8)

plt.tight_layout()
plt.show()

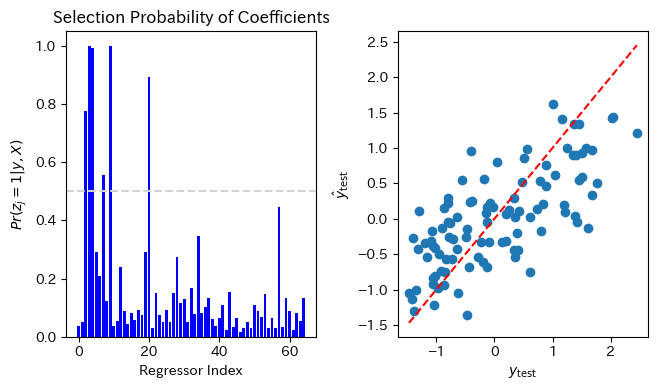
係数がゼロでない確率を示す図、y_{test}の値を\betaのモデル平均推定値に基づく予測値

回帰モデルを以下のように定式化します。

y_i = z_{1}b_{1}x_{i,1} + z_{2}b_{2}x_{i,2} + z_{3}b_{3}x_{i,3} + \dots + z_{p}b_{p}x_{i,p} + \epsilon_{i}

ただし、

z_j \in \{0,1\}\\

とし、z_jはどの回帰係数が0でないかを表現しています。
b_jは正の実数とします。そこで、ギブスサンプラーを用いてそれぞれのz_jを完全条件付き分布から反復的に生成することを考えます。現在のz = (z_{1} \dots z_{p})を所与として、新たなz_jの値をp(z_j|y, X, z_{-j})から生成します。ここではz_{-j}をzからj番目の要素を除いたものを指します。z_jが1になる完全条件付き確率は\frac{o_j}{1+o_j}とします。o_jはz_jが1となる条件付きオッズで以下で与えられます。

o_j = \frac{Pr(z_j = 1|y, X, z_{-j})}{Pr(z_j = 0|y, X, z_{-j})} = \frac{Pr(z_j = 1)}{Pr(z_j = 0)}×\frac{p(y|X, z_{-j}, z_j = 1)}{p(y|X, z_{-j}, z_j = 0)}

ただし、

p(y|X,z) = \pi^{-n/2}\frac{\Gamma([\nu_0+n]/2)}{\Gamma(\nu_0/2)} (1+g)^{-p_z/2}\frac{(\nu_0\sigma^2_0)^{\nu_0/2}}{(\nu_0\sigma^2_0+SSR^{z}_{g})^{(\nu_0+n)/2}}

Xをz_jが非ゼロとなるような変数のみからなる行列X_zとし、\sigma^2はp(\sigma^2|X, y, z)、\betaはp(\beta|X,y,z,\sigma^2)からサンプリングします。ギブスサンプリングの手順は以下のとおりです。

  1. z = z^{(s)}と定める
  2. ランダムな順番でjに対して、z_jをp(z_j|z_{-j}, y, X)からの標本で置き換える
  3. z^{(s+1)} = zと定める
  4. \sigma^{2(s+1)} \sim p(\sigma^2|z^{(s+1)}, y, X)を生成する
  5. \beta^{(s+1)} \sim p(\beta|z^{(s+1)}, \sigma^{2(s+1)},y, X)

図9.7の左図はそれぞれの回帰係数がゼロではない事後確率をプロットしています。右図では横軸にy_{test}、縦軸に\betaのモデル平均推定値に基づく予測値をとったグラフとなっています。

from scipy.special import loggamma

# ベイジアン線形回帰の実装
def lm_gprior(y, X, g=None, nu0=1, s20=None, S=1000):
    n, p = X.shape
    if g is None:
        g = p
    if s20 is None:
        s20 = np.var(y, ddof=1)

    Hg = (g / (g + 1)) * X @ np.linalg.inv(X.T @ X) @ X.T
    SSRg = y.T @ (np.eye(n) - Hg) @ y

    s2 = 1 / stats.gamma.rvs((nu0 + n) / 2, scale=2 / (nu0 * s20 + SSRg), size=S)

    Vb = g * np.linalg.inv(X.T @ X) / (g + 1)
    Eb = Vb @ X.T @ y

    E = np.random.normal(0, np.sqrt(s2), size=(S, p))
    beta = (E @ np.linalg.cholesky(Vb).T) + Eb

    return {'beta': beta, 's2': s2}

# 対数周辺確率の計算
def lpy_X(y, X, g=None, nu0=1, s20=None):
    n, p = X.shape
    if g is None:
        g = len(y)
    if s20 is None:
        s20 = np.mean(y ** 2)
    if p == 0:
        s20 = np.mean(y ** 2)
    H0 = 0
    if p > 0:
        H0 = (g / (g + 1)) * X @ np.linalg.inv(X.T @ X) @ X.T
    SS0 = y.T @ (np.eye(n) - H0) @ y

    return -0.5 * n * np.log(2 * np.pi) + loggamma(0.5 * (nu0 + n)) - loggamma(0.5 * nu0) - 0.5 * p * np.log(1 + g) + \
           0.5 * nu0 * np.log(0.5 * nu0 * s20) - 0.5 * (nu0 + n) * np.log(0.5 * (nu0 * s20 + SS0))

# ベイジアンモデル平均化（BMA）
S = 10000
p = X.shape[1]
BETA = np.zeros((S, p))
Z = np.zeros((S, p))
X_np = X.to_numpy()

for s in range(S):
    for j in np.random.permutation(p):
        z = Z[s - 1].copy()
        zp = z.copy()
        zp[j] = 1 - zp[j]
        lpy_p = lpy_X(y, X_np[:, zp == 1])
        lpy_c = lpy_X(y, X_np[:, z == 1])
        r = (lpy_p - lpy_c) * (-1) ** (zp[j] == 0)
        z[j] = stats.bernoulli.rvs(1 / (1 + np.exp(-r)))
        if z[j] == zp[j]:
            lpy_c = lpy_p

    Z[s] = z
    beta = z.copy()
    if sum(z) > 0:
        beta_gprior = lm_gprior(y, X_np[:, z == 1], S=1)['beta'][0]  
        beta[z == 1] = beta_gprior
    BETA[s] = beta

# BMAによる回帰係数の平均の計算
beta_bma = np.nanmean(BETA, axis=0)
y_te_bma = X_te @ beta_bma

# MSEの計算
mse_bma = np.mean((y_te - y_te_bma) ** 2)

# プロットの作成
plt.figure(figsize=(10, 4))

# プロット1: 各回帰係数がゼロでない事後確率
plt.subplot(1, 3, 1)
mean_selection_probabilities = np.nanmean(Z, axis=0)
plt.bar(range(len(mean_selection_probabilities)), mean_selection_probabilities, color='b', alpha=1)
plt.axhline(y=0.5, color='lightgray', linestyle='--')
plt.xlabel('Regressor Index')
plt.ylabel(r'$Pr(z_j = 1 | y, X)$')
plt.title('Selection Probability of Coefficients')

# プロット2: テストデータの実際の値 vs BMA予測値
plt.subplot(1, 3, 2)
plt.scatter(y_te, y_te_bma)
plt.plot([y_te.min(), y_te.max()], [y_te.min(), y_te.max()], 'r--')
plt.xlabel(r'$y_{\mathrm{test}}$')
plt.ylabel(r'$\hat{y}_{\mathrm{test}}$')

plt.tight_layout()
plt.show()


*この処理は結果が出るまで非常に時間がかかります。

以下のプログラムで\betaモデル平均推定量に基づく予測値\hat{y}_{test}=X\hat{\beta}_{bma}とy_{test}の平均二乗誤差を計算しています。

# MSEの計算
print(mse_bma)
# 0.5256579769839711

普通のOLSや変数減少法後のOLSよりも平均二乗誤差が小さくなっていることがわかります。

最後に

本記事では、「標準ベイズ統計学」の9章で扱われている線形回帰モデルとベイズ的変数選択について、Pythonを用いて実装する方法を詳しく解説してきました。次回は10章「非共役事前分布とメトロポリスヘイスティングスアルゴリズム」を扱います。

DMM Data Blog
DMM Data BlogPublication

DMM.comに所属するデータ分析関連組織の有志によるテックブログです。データ分析に関する知識・技術を発信します。

Discussion