Pythonで再現する標準ベイズ統計学8章

はじめに

本記事では標準ベイズ統計学の8章で掲載されている図表やモデルをPythonで実装する方法に関して説明します。

8章：グループ比較と階層モデリング

標準ベイズ統計学の8章ではグループ間の平均値比較のための統計モデルを紹介し、それを階層的な正規モデルとする方法、さらに平均と分散の両方の不均一性を扱う方法について説明しています。

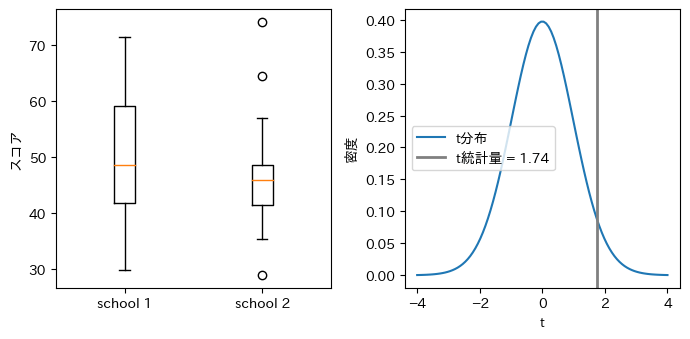
二つの学校の1年生の数学の得点の箱ひげ図と母集団の平均値の同等性を検定するための帰無分布

図8.1の左図は二つの学校の一年生の数学の得点の箱ひげ図、右図は母集団平均の同等性を検定するための帰無分布をプロットしています。右図の縦の垂直線はデータから計算されたt検定量の値を示しています。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ttest_ind, t, norm
import pandas as pd
import japanize_matplotlib

y_school1 = pd.read_csv("./csv/y.school1.csv")
y_school2 = pd.read_csv("./csv/y.school2.csv")

# 各データセットからスコアを抽出
y1 = y_school1['x'].values
y2 = y_school2['x'].values

# 箱ひげ図のプロット
plt.figure(figsize=(7, 3.5))
plt.subplot(1, 2, 1)
plt.boxplot([y1, y2], labels=['school 1', 'school 2'])
plt.ylabel('スコア')

# 必要な統計量の計算
n1 = len(y1)
n2 = len(y2)
mean_y1 = np.mean(y1)
mean_y2 = np.mean(y2)
sd_combined = np.std(np.concatenate([y1, y2]))

# プールされた分散の計算
s2p = (np.var(y1, ddof=1)*(n1-1) + np.var(y2, ddof=1)*(n2-1)) / (n1 + n2 - 2)
tstat = (mean_y1 - mean_y2) / np.sqrt(s2p * (1/n1 + 1/n2))

# t検定の実行
t_test_result = ttest_ind(y1, y2, equal_var=True)

# t分布とt統計量のプロット
ts = np.linspace(-4, 4, 100)
plt.subplot(1, 2, 2)
plt.plot(ts, t.pdf(ts, df=n1+n2-2), label='t分布')
plt.axvline(x=tstat, color='gray', lw=2, label=f't統計量 = {tstat:.2f}')
plt.xlabel('t')
plt.ylabel('密度')
plt.legend()

# プロットの表示
plt.tight_layout()
plt.show()

print(mean_y1)
# 50.81354838709678
print(mean_y2) 
# 46.15071428571428
print(sd_combined)
# 10.357445837952747
print(s2p)
# 105.4290999191527
print(tstat)
# 1.7418211969266815
print(t_test_result)
# Ttest_indResult(statistic=1.7418211969266812, pvalue=0.08693402825485134))

$\bar{y}_1$が50.81、$\bar{y}_2$が46.15、t統計量の値は1.74、P値が約0.087となっているため、書籍の内容を再現できているといえます。

箱ひげ図が少し書籍と異なるのはRとmatplotlibの仕様の差であるため、ここではあまりこだわりすぎず上記のプロットで再現できたことにします笑

$\mu$と$\delta$の事前分布と事後分布

二つの学校の数学の平均得点の差（ここでは$\delta = \frac{\theta_1 - \theta_2}{2}$とする）が有意か否かをベイズで分析する際には以下のような完全条件付き分布を利用する。

$$\{\mu|y_1, y_2, \delta, \sigma^2\} \sim normal(\mu_n, \gamma_n^2) \\$$

$$\mu_n = \gamma_n^2 × [\mu_0/\gamma_n^2 + \Sigma^{n_1}_{i=1}(y_{i,1}-\delta)/\sigma^2 + \Sigma^{n_2}_{i=1}(y_{i,2}+\delta)/\sigma^2]\\ \gamma_n^{2} = [\frac{1}{\gamma_0^{2}} + \frac{(n_1+n_2)}{\sigma^2}]^{-1}\\$$

$$\{\delta|y_1, y_2, \mu, \sigma^2\} \sim normal(\delta_n, \tau_n^2) \\$$

$$\delta_n = \tau_n^2 × [\delta_0/\tau_0^2 + \Sigma^{n_1}_{i=1}(y_{i,1}-\mu)/\sigma^2 - \Sigma^{n_2}_{i=1}(y_{i,2}-\mu)/\sigma^2]\\ \gamma_n^{2} = [\frac{1}{\tau_0^{2}} + \frac{(n_1+n_2)}{\sigma^2}]^{-1}\\$$

$$\{\sigma^2|y_1, y_2, \mu, \delta\} \sim inverse-gamma(\frac{\nu_n}{2}, \frac{\nu_n\sigma^2_{n}}{2})$$

$$\nu_n = \nu_0 + n_1 + n_2 \\ \nu_n\sigma^2_n = \nu_0\sigma^2_0 + \Sigma(y_i,1 -[\mu + \delta])^2 + \Sigma(y_i,2 -[\mu - \delta])^2$$

図8.2に$\mu$、$\delta$の周辺事後分布を示しています。

import seaborn as sns
from scipy.stats import gamma, norm

# 事前分布のパラメータ
mu0, g02 = 50, 625
del0, t02 = 0, 625
s20, nu0 = 100, 1

# 初期値
mu = (mean_y1 + mean_y2) / 2
del_ = (mean_y1 - mean_y2) / 2

# Gibbsサンプラーのパラメータ
MU, DEL, S2 = [], [], []
Y12 = []

np.random.seed(1)
for s in range(5000):
    # s2の更新
    s2 = 1 / np.random.gamma((nu0 + n1 + n2) / 2,
                             scale=2 / (nu0 * s20 + np.sum((y1 - mu - del_)**2) + np.sum((y2 - mu + del_)**2)))

    # muの更新
    var_mu = 1 / (1 / g02 + (n1 + n2) / s2)
    mean_mu = var_mu * (mu0 / g02 + np.sum(y1 - del_) / s2 + np.sum(y2 + del_) / s2)
    mu = np.random.normal(mean_mu, np.sqrt(var_mu))

    # delの更新
    var_del = 1 / (1 / t02 + (n1 + n2) / s2)
    mean_del = var_del * (del0 / t02 + np.sum(y1 - mu) / s2 - np.sum(y2 - mu) / s2)
    del_ = np.random.normal(mean_del, np.sqrt(var_del))

    # パラメータ値の保存
    MU.append(mu)
    DEL.append(del_)
    S2.append(s2)
    Y12.append(np.random.normal(mu + np.array([1, -1]) * del_, np.sqrt(s2), 2))

# Y12をnumpy配列に変換して操作を容易にする
Y12 = np.array(Y12)

# プロット
plt.figure(figsize=(7, 3.5))

# MUとDELの密度プロット
plt.subplot(1, 2, 1)
sns.kdeplot(MU, bw_adjust=2, label='事後分布')
ds = np.linspace(mu0 - np.sqrt(g02), mu0 + np.sqrt(g02), 100)
plt.plot(ds, norm.pdf(ds, mu0, np.sqrt(g02)), label='事前分布', color='gray', lw=2)
plt.xlim(mu0 - np.sqrt(g02), mu0 + np.sqrt(g02))
plt.xlabel(r'$\mu$')
plt.ylabel('密度')
plt.title('')
plt.legend()

plt.subplot(1, 2, 2)
sns.kdeplot(DEL, bw_adjust=2, label='事後分布')
ds = np.linspace(-np.sqrt(t02), np.sqrt(t02), 100)
plt.plot(ds, norm.pdf(ds, 0, np.sqrt(t02)), label='事前分布', color='gray', lw=2)
plt.xlim(-np.sqrt(t02), np.sqrt(t02))
plt.xlabel(r'$\delta$')
plt.ylabel('密度')
plt.title('')
plt.legend()

plt.tight_layout()
plt.show()

事後統計量の計算

DEL_quantiles = np.quantile(DEL, [0.025, 0.5, 0.975])
DEL_double_quantiles = np.quantile(np.array(DEL) * 2, [0.025, 0.5, 0.975])
mean_DEL_positive = np.mean(np.array(DEL) > 0)
mean_Y12_1_greater_Y12_2 = np.mean(Y12[:, 0] > Y12[:, 1])

print(DEL_quantiles)
# [-0.25490674  2.30998435  4.98943956]
print(DEL_double_quantiles) 
# [-0.50981349  4.6199687   9.97887912]
print(mean_DEL_positive)
# 0.9594
print(mean_Y12_1_greater_Y12_2)
# 0.6304

$\delta$ の95%事後信用区間は(-0.25, 4.98)です。また、2×$\delta$（2校の平均スコアの差）の95%事後信用区間は(-0.50, 9.97)です。
$Pr(\theta_1 > \theta_2|y_1, y_2)=Pr(\delta >0 | y_1, y_2)=0.9594$であることから、学校1の母平均が学校2の母平均よりも高いことがわかります。
ただし、これと「学校1から無作為に選ばれた生徒が学校2から選ばれた生徒よりも高い得点を得る確率」は異なります。この確率$Pr(Y_1 > Y_2|y_1, y_2)=0.6304$となっています。

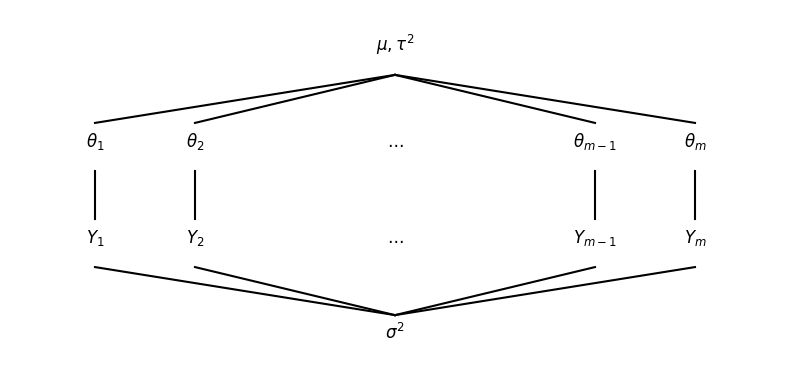
階層正規モデルのグラフ表現

図8.3は階層正規モデルのグラフ表現です。Pythonでの実装だけ以下に記載しておきます。

# スクリプトで指定された図8.3のプロットを作成
plt.figure(figsize=(8, 4))

# プロット領域の設定
plt.plot([0.15, 0.85], [0.15, 0.85], 'w')  # 領域を設定するための見えないプロット
plt.axis('off')

# 階層モデルのテキストとセグメント
plt.text(0.5, 0.8, r'$\mu, \tau^2$', fontsize=12, ha='center')
plt.text(0.2, 0.6, r'$\theta_1$', fontsize=12, ha='center')
plt.text(0.3, 0.6, r'$\theta_2$', fontsize=12, ha='center')
plt.text(0.5, 0.6, r'$\ldots$', fontsize=12, ha='center')
plt.text(0.7, 0.6, r'$\theta_{m-1}$', fontsize=12, ha='center')
plt.text(0.8, 0.6, r'$\theta_m$', fontsize=12, ha='center')

# mu/tau^2とthetasを結ぶセグメント
plt.plot([0.5, 0.2], [0.75, 0.65], 'k-')
plt.plot([0.5, 0.3], [0.75, 0.65], 'k-')
plt.plot([0.5, 0.7], [0.75, 0.65], 'k-')
plt.plot([0.5, 0.8], [0.75, 0.65], 'k-')

# サンプル平均のテキストとセグメント
plt.text(0.2, 0.4, r'$\bar{y}_1$', fontsize=12, ha='center')
plt.text(0.3, 0.4, r'$\bar{y}_2$', fontsize=12, ha='center')
plt.text(0.5, 0.4, r'$\ldots$', fontsize=12, ha='center')
plt.text(0.7, 0.4, r'$\bar{y}_{m-1}$', fontsize=12, ha='center')
plt.text(0.8, 0.4, r'$\bar{y}_m$', fontsize=12, ha='center')

# thetasとサンプル平均を結ぶセグメント
plt.plot([0.2, 0.2], [0.55, 0.45], 'k-')
plt.plot([0.3, 0.3], [0.55, 0.45], 'k-')
plt.plot([0.7, 0.7], [0.55, 0.45], 'k-')
plt.plot([0.8, 0.8], [0.55, 0.45], 'k-')

# sigma^2とサンプル平均を結ぶセグメント
plt.plot([0.5, 0.2], [0.25, 0.35], 'k-')
plt.plot([0.5, 0.3], [0.25, 0.35], 'k-')
plt.plot([0.5, 0.7], [0.25, 0.35], 'k-')
plt.plot([0.5, 0.8], [0.25, 0.35], 'k-')

# sigma^2のテキスト
plt.text(0.5, 0.2, r'$\sigma^2$', fontsize=12, ha='center')

plt.tight_layout()
plt.show()

数学試験の学校平均得点の順位

1年性の生徒数が400人以上の大規模な100の都市部の公立高校における1年生を対象にした数学試験のデータにおいて、同じ学校の生徒の得点を共通の縦棒に並べて表示したものが図8.4です。

y_school_mathscore = pd.read_csv("./csv/Y.school.mathscore.csv")
# データをリスト形式に整理し、必要な統計量を計算する
J = y_school_mathscore['school'].max()
Y = [y_school_mathscore[y_school_mathscore['school'] == j]['mathscore'].values for j in range(1, J + 1)]

ybar = [np.mean(scores) for scores in Y]
n = [len(scores) for scores in Y]

# プロットを作成する
plt.figure(figsize=(7, 3.5))
plt.xlabel('数学試験の学校平均得点の順位')
plt.ylabel('数学スコア')
plt.ylim(min([min(scores) for scores in Y]), max([max(scores) for scores in Y]))

# 各学校のポイントとセグメントをプロットする
for l in range(J):
    j = np.argsort(ybar)[l]
    plt.scatter(np.repeat(l + 1, n[j]), Y[j], s=10)
    plt.plot([l + 1, l + 1], [min(Y[j]), max(Y[j])], color='black')

# 全体の平均を表す水平線
plt.axhline(np.mean(ybar), color='red', linestyle='--')

plt.tight_layout()
plt.show()

標本平均の経験分布と標本平均とサンプルサイズの関係

図8.5の左図は数学試験のデータの標本平均の経験分布、右図は標本平均とサンプルサイズの関係をプロットしています。

# プロットの設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

# 一つ目のプロット：サンプル平均のヒストグラム
ax1.hist(ybar, edgecolor='black', alpha=0.7, color='skyblue')
ax1.set_xlabel('sample mean', fontsize=12)
ax1.tick_params(axis='both', which='major', labelsize=10)

# 二つ目のプロット：samplesizeとsample meanの散布図
ax2.scatter(n, ybar, alpha=0.6, edgecolors='none', color='blue', s=90)
ax2.set_xlabel('samplesize', fontsize=12)
ax2.set_ylabel('sample mean', fontsize=12)
ax2.tick_params(axis='both', which='major', labelsize=10)

# 軸の範囲を設定
ax2.set_xlim(0, max(n) + 1)
ax2.set_ylim(min(ybar) - 1, max(ybar) + 1)

plt.tight_layout()
plt.show()

$\mu$, $\sigma^2$, $\tau^2$のMCMCサンプルの箱ひげ図

図8.6が掲載されている8.4.1節でのギブスサンプリングでは、学校内分散・学校間分散$\sigma^2_0=\tau^2_0=100$、過大評価する可能性を考慮し$\nu_0 = \eta_0 = 1$と設定しています。また、全校平均は50、各学校の平均が全校平均とそこまで大きな差がないことを考慮し、分散を25としています。各学校の平均点を計算するために、以下のようなギブスサンプリングを用いています。

$$\mu^{(s+1)} \sim p(\mu|\theta^{(s)}_{1} \dots \theta^{(s)}_{m}, \tau^{2(s)}) \\ \tau^{2(s+1)} \sim p(\tau^{2}|\theta^{(s)}_{1} \dots \theta^{(s)}_{m}, \mu^{2(s+1)}) \\ \sigma^{2(s+1)} \sim p(\sigma^2|\theta^{(s)}_{1} \dots \theta^{(s)}_{m}, y_1 \dots y_m)\\ 各j \in \{1 \dots m\}に対して\theta^{(s+1}_{j} \sim p(\theta_j|\mu^{(s+1)}, \tau^{2(s+1)}, \sigma^{2(s+1)}, y_j)$$

図8.6では$\mu, \sigma^2, \tau^2$のMCMCのサンプルの箱ひげ図をプロットしています。以下のPythonでの実装では箱ひげ図ではなく、普通にMCMCのサンプルをプロットしました。プロットを見て定常性を確認するだけですので、特に問題ないと思います。

# 弱情報事前分布の設定
nu0, s20 = 1, 100
eta0, t20 = 1, 100
mu0, g20 = 50, 25

# 初期値の設定
m = len(Y)
n = [len(y) for y in Y]
ybar = [np.mean(y) for y in Y]
sv = [np.var(y, ddof=1) for y in Y]

theta = np.array(ybar)
sigma2 = np.mean(sv)
mu = np.mean(theta)
tau2 = np.var(theta, ddof=1)

# MCMCのセットアップ
np.random.seed(1)
S = 5000
THETA = np.zeros((S, m))
MST = np.zeros((S, 3))

# MCMCアルゴリズム
for s in range(S):
    # thetaの新しい値をサンプリング
    for j in range(m):
        vtheta = 1 / (n[j] / sigma2 + 1 / tau2)
        etheta = vtheta * (ybar[j] * n[j] / sigma2 + mu / tau2)
        theta[j] = np.random.normal(etheta, np.sqrt(vtheta))

    # sigma2の新しい値をサンプリング
    nun = nu0 + np.sum(n)
    ss = nu0 * s20 + sum([np.sum((Y[j] - theta[j])**2) for j in range(m)])
    sigma2 = 1 / np.random.gamma(nun / 2, 2 / ss)

    # muの新しい値をサンプリング
    vmu = 1 / (m / tau2 + 1 / g20)
    emu = vmu * (m * np.mean(theta) / tau2 + mu0 / g20)
    mu = np.random.normal(emu, np.sqrt(vmu))

    # tau2の新しい値をサンプリング
    etam = eta0 + m
    ss = eta0 * t20 + np.sum((theta - mu)**2)
    tau2 = 1 / np.random.gamma(etam / 2, 2 / ss)

    # 結果の保存
    THETA[s, :] = theta
    MST[s, :] = [mu, sigma2, tau2]

# ボックスプロット分析のための関数
def mcmc_boxplot_analysis(data, param_names, num_groups=10):
    n_params = data.shape[1]
    n_iterations = data.shape[0]
    group_size = n_iterations // num_groups

    fig, axes = plt.subplots(1, n_params, figsize=(15, 5))

    for i, param in enumerate(param_names):
        grouped_data = [data[j:j+group_size, i] for j in range(0, n_iterations, group_size)]
        
        bp = axes[i].boxplot(grouped_data, positions=range(1, num_groups+1))
        axes[i].set_xlabel('iteration')
        axes[i].set_ylabel(param)
        axes[i].set_title(f'{param}')
        
        # x軸の目盛りを実際のイテレーション数で表示
        tick_labels = [f'{500 * j}' for j in range(1, num_groups+1)]
        axes[i].set_xticklabels(tick_labels)
        
        # x軸ラベルを読みやすくするために回転
        plt.setp(axes[i].get_xticklabels(), rotation=45, ha='right')
        
        # y軸の範囲を画像により近くなるように調整
        if param == 'μ':
            axes[i].set_ylim(46, 50)
        elif param == 'σ²':
            axes[i].set_ylim(75, 95)
        elif param == 'τ²':
            axes[i].set_ylim(15, 45)

    plt.tight_layout()
    plt.show()

# ボックスプロット分析の実行
param_names = ['μ', 'σ²', 'τ²']
mcmc_boxplot_analysis(MST, param_names)

周辺事後分布と2.5%、50%、97.5%分位点

図8.7では$\{\mu, \sigma^2, \tau^2\}$の事後密度のモンテカルロ近似を示しています。

from scipy.stats import gaussian_kde

# MSTの平均
mean_MST = np.mean(MST, axis=0)

# 図8.7: 分位数付きの密度プロット
plt.figure(figsize=(10, 4))
for i, param in enumerate(['$\mu$', r'$\sigma^2$', r'$\tau^2$']):
    plt.subplot(1, 3, i+1)
    density = gaussian_kde(MST[:, i])
    xs = np.linspace(min(MST[:, i]), max(MST[:, i]), 200)
    plt.plot(xs, density(xs), lw=2)
    plt.xlabel(param)
    plt.ylabel(f'p({param}|y)')
    quantiles = np.quantile(MST[:, i], [0.025, 0.5, 0.975])
    for q in quantiles:
        plt.axvline(x=q, color='gray', linestyle='--')
    plt.title('')
    plt.tight_layout()

plt.show()

print(mean_MST[0])
print(np.sqrt(mean_MST[1]))
print(np.sqrt(mean_MST[2]))

$\mu, \sigma^2, \tau^2$の事後平均はそれぞれ

$$\mu = 48.12970230330388 \\ \sigma^2 = 9.21070810466296 \\ \tau^2 = 4.985347724593711$$

となっています。学校内の95%の得点が$4×9.21 \approx 37$点以下の差に収まっており、学校平均点の95%は$4×4.98\approx20$点以下の差に収まっています。

サンプルサイズの関数としての縮小量

$\theta_j$の期待値は以下のようになります。

$$E[\theta_j|y_j, \mu, \tau, \sigma] = \frac{\bar{y}_jn_j/\sigma^2 + \mu/\tau^2}{n_j/\sigma^2+1/\tau^2}$$

したがって、$\theta_j$の期待値は$n_j$に応じた量だけ$\bar{y}_j$から$\mu$に引っ張られます（縮小）。図8.8の左図は$\bar{y}_j$に対する$\hat{\theta}_j = E[\theta_j|y_1 \dots y_m]$の散布図です。右図は横軸にサンプルサイズ、縦軸に縮小量をとった図となっています。

# 各学校のTHETAの平均値（theta_hat）を計算
theta_hat = np.mean(THETA, axis=0)

# Figure 8.8のプロットを作成
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 7))

# 左側のサブプロット: ybar vs theta_hat
ax1.scatter(ybar, theta_hat, alpha=0.6, edgecolors='none', color='blue', s=90)
ax1.plot([min(ybar), max(ybar)], [min(ybar), max(ybar)], 'k-', lw=1)
ax1.set_xlabel(r'$\bar{y}$', fontsize=12)
ax1.set_ylabel(r'$\hat{\theta}$', fontsize=12)
ax1.set_xlim(min(ybar)-1, max(ybar)+1)
ax1.set_ylim(min(theta_hat)-1, max(theta_hat)+1)
ax1.tick_params(axis='both', which='major', labelsize=10)

# 右側のサブプロット: サンプルサイズ vs (ybar - theta_hat)
difference = np.array(ybar) - theta_hat
ax2.scatter(n, difference, alpha=0.6, edgecolors='none', color='blue', s=90)
ax2.axhline(y=0, color='k', linestyle='-', lw=1)
ax2.set_xlabel('samplesize', fontsize=12)
ax2.set_ylabel(r'$\bar{y} - \hat{\theta}$', fontsize=12)
ax2.set_xlim(0, max(n)+1)
ax2.set_ylim(min(difference)-1, max(difference)+1)
ax2.tick_params(axis='both', which='major', labelsize=10)

plt.tight_layout()
plt.show()

左図の直線の傾きは1となっています。散布図のプロットは全体的にやや傾きは1よりやや小さい直線に沿ったものであることがわかります。$\bar{y}$の値が大きいと$\theta_j$の値よりも小さく、$\bar{y}_j$の値が小さいと$\theta_j$の値よりも大きくなっています。右図を見るとサンプルサイズが大きいと縮小量は小さく、サンプルサイズが小さいと縮小量は大きくなっています。

2校のデータと事後分布

図8.9では学校46と学校82の$\theta_j$の事後分布です。学校46はサンプルサイズが21人であり、学校は82はサンプルサイズは5人です。

# プロットで強調表示する学校
idx = [46, 82]

mean_MST_corrected = np.mean(MST, axis=0)

# まず、2つの学校のTHETAサンプルの密度推定を計算する
theta_46_density = gaussian_kde(THETA[:, idx[0] - 1])
theta_82_density = gaussian_kde(THETA[:, idx[1] - 1])

# THETAサンプルと実際のスコアの範囲に基づいてプロットの範囲を定義する
x_range = np.linspace(
    min(np.concatenate((THETA[:, idx[0] - 1], THETA[:, idx[1] - 1], Y[idx[0] - 1], Y[idx[1] - 1]))),
    max(np.concatenate((THETA[:, idx[0] - 1], THETA[:, idx[1] - 1], Y[idx[0] - 1], Y[idx[1] - 1]))),
    200
)

# 密度をプロットする
plt.figure(figsize=(7, 5))
plt.plot(x_range, theta_46_density(x_range), color='black', lw=2)
plt.plot(x_range, theta_82_density(x_range), color='gray', lw=2)

# muの平均値のための垂直線を追加
plt.axvline(mean_MST_corrected[0], color='red', linestyle='--', lw=2)

# 実際のスコアをプロットの下部に点として表示
plt.scatter(Y[idx[0] - 1], np.full_like(Y[idx[0] - 1], -0.01666), color='black', s=10)
plt.scatter(Y[idx[1] - 1], np.full_like(Y[idx[1] - 1], -0.0333), color='gray', s=10)

# サンプル平均をプロットの下部により大きな点として追加
plt.scatter(ybar[idx[0] - 1], -0.01666, color='black', s=30)
plt.scatter(ybar[idx[1] - 1], -0.0333, color='gray', s=30)

# 2つのポイントグループのための水平線を追加
plt.axhline(-0.01666, color='black', lw=1)
plt.axhline(-0.0333, color='gray', lw=1)

# y軸の限界を設定し、y軸の目盛りを削除
plt.ylim(-0.05, 0.22)
plt.yticks([])

# 凡例を追加
plt.legend(['学校46', '学校82', r'E[$\mu|y$]'], loc='upper right')

# x軸のラベルを設定
plt.xlabel('数学スコア')

plt.show()

不均一な平均・分散構造をもつ階層正規モデルのグラフ表示

図8.10では不均一な平均・分散構造をもつ階層正規モデルのグラフをプロットしています。この図をpythonで書く意味があるのかわかりませんが、一応実装を下に載せておきます。実装の解説はしません。

plt.figure(figsize=(8, 6))


plt.plot([0.15, 0.85], [0.15, 0.85], 'w')  
plt.axis('off')


plt.text(0.5, 0.8, r'$\mu, \tau^2$', fontsize=12, ha='center')
plt.text(0.2, 0.6, r'$\theta_1$', fontsize=12, ha='center')
plt.text(0.3, 0.6, r'$\theta_2$', fontsize=12, ha='center')
plt.text(0.5, 0.6, r'$\ldots$', fontsize=12, ha='center')
plt.text(0.7, 0.6, r'$\theta_{m-1}$', fontsize=12, ha='center')
plt.text(0.8, 0.6, r'$\theta_m$', fontsize=12, ha='center')


plt.plot([0.5, 0.2], [0.75, 0.65], 'k-')
plt.plot([0.5, 0.3], [0.75, 0.65], 'k-')
plt.plot([0.5, 0.7], [0.75, 0.65], 'k-')
plt.plot([0.5, 0.8], [0.75, 0.65], 'k-')


plt.text(0.2, 0.4, r'$Y_1$', fontsize=12, ha='center')
plt.text(0.3, 0.4, r'$Y_2$', fontsize=12, ha='center')
plt.text(0.5, 0.4, r'$\ldots$', fontsize=12, ha='center')
plt.text(0.7, 0.4, r'$Y_{m-1}$', fontsize=12, ha='center')
plt.text(0.8, 0.4, r'$Y_m$', fontsize=12, ha='center')


plt.plot([0.2, 0.2], [0.55, 0.45], 'k-')
plt.plot([0.3, 0.3], [0.55, 0.45], 'k-')
plt.plot([0.7, 0.7], [0.55, 0.45], 'k-')
plt.plot([0.8, 0.8], [0.55, 0.45], 'k-')


plt.plot([0.2, 0.2], [0.25, 0.35], 'k-')
plt.plot([0.3, 0.3], [0.25, 0.35], 'k-')
plt.plot([0.7, 0.7], [0.25, 0.35], 'k-')
plt.plot([0.8, 0.8], [0.25, 0.35], 'k-')


plt.text(0.2, 0.15, r'$\sigma^2_1$', fontsize=12, ha='center')
plt.text(0.3, 0.15, r'$\sigma^2_2$', fontsize=12, ha='center')
plt.text(0.5, 0.15, r'$\ldots$', fontsize=12, ha='center')
plt.text(0.7, 0.15, r'$\sigma^2_{m-1}$', fontsize=12, ha='center')
plt.text(0.8, 0.15, r'$\sigma^2_m$', fontsize=12, ha='center')


plt.plot([0.5, 0.2], [-0.05, 0.1], 'k-')
plt.plot([0.5, 0.3], [-0.05, 0.1], 'k-')
plt.plot([0.5, 0.7], [-0.05, 0.1], 'k-')
plt.plot([0.5, 0.8], [-0.05, 0.1], 'k-')


plt.text(0.5, -0.1, r'$\nu^2_0, \sigma^2_0$', fontsize=12, ha='center')

plt.tight_layout()
plt.show()

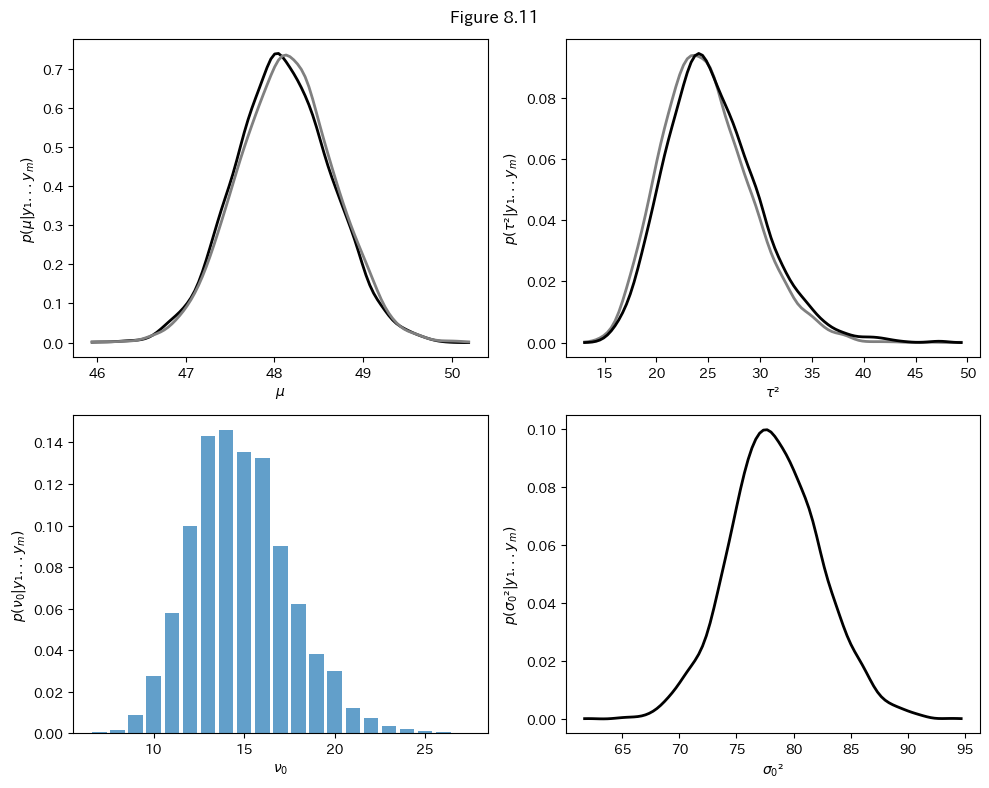
グループ間で異なるパラメータの事後分布

この図は、階層モデルにおける4つの重要なパラメータの事後分布を視覚化しています。
まず、$\mu$（全体平均）の分布は、全グループの平均値を表現しており、データ全体の中心傾向を示します。この分布の形状と位置から、分析対象全体の一般的な特性を把握できます。
次に、$\tau^2$（グループ間分散）の分布は、グループ間のばらつきを表現します。この値が大きいほど、グループ間の差異が顕著であることを意味し、小さいほどグループ間の類似性が高いことを示唆します。
$\nu_0$（自由度パラメータ）の分布は、分散の事前分布の形状を制御するパラメータです。この値が大きいほど、グループ間で分散が類似していることを示唆し、小さい値はグループ間で分散が大きく異なる可能性を示します。
最後に、$\sigma_0^2$（スケールパラメータ）の分布は、分散の事前分布のスケールを制御します。このパラメータは、グループ内分散の全体的な大きさを表現し、データのばらつきの程度を総合的に示します。
これらのパラメータの事後分布を同時に観察することで、データの階層構造や、グループ間・グループ内の変動性について、包括的な理解を得ることができます。この分析により、複雑なデータ構造における潜在的なパターンや関係性を明らかにすることが可能となります。

from scipy.stats import gamma, norm
from scipy.special import gammaln

np.random.seed(90)

# 弱情報事前分布
nu0, s20 = 1, 100
eta0, t20 = 1, 100
mu0, g20 = 50, 25
a0, b0, wnu0 = 1, 1/100, 1

# 初期値の設定
m = len(Y)
n = np.array([len(y) for y in Y])
ybar = np.array([np.mean(y) for y in Y])
sv = np.array([np.var(y) for y in Y])
theta = ybar.copy()
sigma2 = sv.copy()
mu = np.mean(theta)
tau2 = np.var(theta)
s20 = 1 / np.mean(1 / sv)

# MCMCの設定
S = 5000
SIGMA2 = np.zeros((S, m))
THETA = np.zeros((S, m))
MTSN = np.zeros((S, 4))
s2_pp = []
nu0s = np.arange(1, 5001)

# MCMCアルゴリズム
for s in range(S):
    # thetaの更新
    for j in range(m):
        vtheta = 1 / (n[j] / sigma2[j] + 1 / tau2)
        etheta = vtheta * (ybar[j] * n[j] / sigma2[j] + mu / tau2)
        theta[j] = np.random.normal(etheta, np.sqrt(vtheta))

    # sigma2の更新
    for j in range(m):
        nun = nu0 + n[j]
        ss = nu0 * s20 + np.sum((Y[j] - theta[j])**2)
        sigma2[j] = 1 / np.random.gamma(nun / 2, 2 / ss)

    # s20の更新
    s20 = np.random.gamma(a0 + m * nu0 / 2, 1 / (b0 + nu0 * np.sum(1 / sigma2) / 2))

    # nu0の更新
    lpnu0 = 0.5 * nu0s * m * np.log(s20 * nu0s / 2) - m * gammaln(nu0s / 2) + \
            (nu0s / 2 - 1) * np.sum(np.log(1 / sigma2)) - \
            nu0s * s20 * np.sum(1 / sigma2) / 2 - wnu0 * nu0s
    p_nu0 = np.exp(lpnu0 - np.max(lpnu0))
    nu0 = np.random.choice(nu0s, p=p_nu0 / np.sum(p_nu0))

    # muの更新
    vmu = 1 / (m / tau2 + 1 / g20)
    emu = vmu * (m * np.mean(theta) / tau2 + mu0 / g20)
    mu = np.random.normal(emu, np.sqrt(vmu))

    # tau2の更新
    etam = eta0 + m
    ss = eta0 * t20 + np.sum((theta - mu)**2)
    tau2 = 1 / np.random.gamma(etam / 2, 2 / ss)

    # 結果の保存
    THETA[s] = theta
    SIGMA2[s] = sigma2
    MTSN[s] = [mu, tau2, s20, nu0]
    s2_pp.append(1 / np.random.gamma(nu0 / 2, 2 / (nu0 * s20)))

# 図8.11
fig, axes = plt.subplots(2, 2, figsize=(10, 8))

# μの分布
mu_kde1 = gaussian_kde(MTSN[:, 0])
mu_kde2 = gaussian_kde(MST[:, 0])
mu_x = np.linspace(min(min(MTSN[:, 0]), min(MST[:, 0])), max(max(MTSN[:, 0]), max(MST[:, 0])), 100)
axes[0, 0].plot(mu_x, mu_kde1(mu_x), 'k-', linewidth=2)
axes[0, 0].plot(mu_x, mu_kde2(mu_x), 'gray', linewidth=2)
axes[0, 0].set_xlabel('μ')
axes[0, 0].set_ylabel('p(μ|y₁...y_m)')

# τ²の分布
tau2_kde1 = gaussian_kde(MST[:, 2])
tau2_kde2 = gaussian_kde(MTSN[:, 1])
tau2_x = np.linspace(min(min(MST[:, 2]), min(MTSN[:, 1])), max(max(MST[:, 2]), max(MTSN[:, 1])), 100)
axes[0, 1].plot(tau2_x, tau2_kde1(tau2_x), 'gray', linewidth=2)
axes[0, 1].plot(tau2_x, tau2_kde2(tau2_x), 'k-', linewidth=2)
axes[0, 1].set_xlabel('τ²')
axes[0, 1].set_ylabel('p(τ²|y₁...y_m)')

# ν₀の分布 (棒グラフのまま)
nu0_values, nu0_counts = np.unique(MTSN[:, 3].astype(int), return_counts=True)
axes[1, 0].bar(nu0_values, nu0_counts / len(MTSN), alpha=0.7)
axes[1, 0].set_xlabel('ν₀')
axes[1, 0].set_ylabel('p(ν₀|y₁...y_m)')

# σ₀²の分布
s20_kde = gaussian_kde(MTSN[:, 2])
s20_x = np.linspace(min(MTSN[:, 2]), max(MTSN[:, 2]), 100)
axes[1, 1].plot(s20_x, s20_kde(s20_x), 'k-', linewidth=2)
axes[1, 1].set_xlabel('σ₀²')
axes[1, 1].set_ylabel('p(σ₀²|y₁...y_m)')

plt.tight_layout()
plt.show()

縮小度とサンプルサイズの関係

この図は、ベイズ階層モデルの重要な特徴である「縮小効果」を2つの異なる視点から視覚化しています。
左側のプロットは、サンプル分散($s^2$)と推定された真の分散($\sigma^2$)の関係を表しています。横軸にサンプル分散、縦軸に推定分散をとり、完全な一致を示す $y = x$ の赤い点線も描かれています。データ点がこの線から乖離するほど、推定値がサンプル分散から「縮小」されていることを意味します。
右側のプロットは、サンプルサイズと縮小度の関係を示しています。横軸にサンプルサイズ、縦軸に縮小の程度をとっています。このプロットから、サンプルサイズが小さいほど縮小度が大きくなる傾向が観察できます。これは、小さなサンプルサイズのグループでは、推定値が全体平均に向けてより強く調整されることを示唆しています。

# 平均値の計算
sigma2_hat = np.mean(SIGMA2, axis=0)

# 図8.12のプロット
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 7))

# 左側のプロット: s² vs σ²
ax1.scatter(sv, sigma2_hat, alpha=0.6, edgecolors='none', color='blue', s=90)
ax1.plot([40, 160], [40, 160], 'k-', lw=1)
ax1.set_xlabel('$s^2$', fontsize=12)
ax1.set_ylabel('$\hat{\sigma}^2$', fontsize=12)
ax1.set_xlim(15, 140)
ax1.set_ylim(50, 140)
ax1.set_xticks(np.arange(50, 201, 50))
ax1.set_yticks(np.arange(60, 161, 20))
ax1.tick_params(axis='both', which='major', labelsize=10)


# 右側のプロット: サンプルサイズ vs 縮小度
shrinkage = sv - sigma2_hat
ax2.scatter(n, shrinkage, alpha=0.6, edgecolors='none', color='blue', s=90)
ax2.axhline(y=0, color='k', linestyle='-', lw=1)
ax2.set_xlabel('sample size', fontsize=12)
ax2.set_ylabel('$s^2 - \hat{\sigma}^2$', fontsize=12)
ax2.set_xlim(0, 30)
ax2.set_ylim(-40, 30)
ax2.set_xticks(np.arange(5, 36, 5))
ax2.set_yticks(np.arange(-30, 31, 10))
ax2.tick_params(axis='both', which='major', labelsize=10)

# 全体的な調整
plt.tight_layout()

plt.show()

なんか右側のプロットが書籍と若干異なるのですが、もうmatplotlibと格闘するのに疲れたので、これでよしとしますww

最後に

本記事では、「標準ベイズ統計学」の8章で扱われているグループ比較と階層モデリングについて、Pythonを用いた実装と可視化を行いました。この実装を通じて、ベイズ階層モデルの特徴である縮小効果や、グループ間・グループ内の変動性をより直感的に理解できることを期待しています。