Pythonで再現する標準ベイズ統計学4章

はじめに

本記事では標準ベイズ統計学の4章で掲載されている図表やモデルをPythonで実装する方法に関して説明します。

4章：モンテカルロ近似

この章ではモンテカルロ法を紹介しています。例えば、モンテカルロ法は以下のような複雑な状況で活躍します。

1.特定の条件を満たすパラメータの確率を知りたい場合
2.パラメータの複雑な関数の平均や標準偏差を計算したい場合
3.欠測データや未観測データの予測に興味がある場合
4.複数の母集団を比較し、その差や比、最大値の分布を調べたい場合

本ブログでは、モンテカルロ法をPythonで実装していきます。

gamma(68,45)分布のモンテカルロ近似のヒストグラムとカーネル密度推定

図4.1はガンマ分布gamma(68, 45)の密度に対するモンテカルロ近似と比較のための真の密度関数を示しています。モンテカルロ標本の経験分布はSが大きくなるにつれて、真の密度の良い近似を与えています。Pythonでの実装は以下のとおりです。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gamma, gaussian_kde

# パラメータ設定
np.random.seed(3)
a = 68
b = 45
theta_support = np.linspace(0, 3, 100)

# ガンマ分布からのサンプル
theta_sim10 = np.random.gamma(a, 1/b, 10)
theta_sim100 = np.random.gamma(a, 1/b, 100)
theta_sim1000 = np.random.gamma(a, 1/b, 1000)

# プロット設定
fig, axs = plt.subplots(2, 3, figsize=(12, 6))
xlim = (0.75, 2.25)
ylim = (0, 2.5)

# ヒストグラムのプロット
axs[0, 0].hist(theta_sim10, density=True, bins='auto', color='lightblue', edgecolor='black')
axs[0, 0].plot(theta_support, gamma.pdf(theta_support, a, scale=1/b), color='gray', lw=2)
axs[0, 0].text(2.1, 2.25, 'S=10')

axs[0, 1].hist(theta_sim100, density=True, bins='auto', color='lightblue', edgecolor='black')
axs[0, 1].plot(theta_support, gamma.pdf(theta_support, a, scale=1/b), color='gray', lw=2)
axs[0, 1].text(2.1, 2.25, 'S=100')

axs[0, 2].hist(theta_sim1000, density=True, bins='auto', color='lightblue', edgecolor='black')
axs[0, 2].plot(theta_support, gamma.pdf(theta_support, a, scale=1/b), color='gray', lw=2)
axs[0, 2].text(2.1, 2.25, 'S=1000')

# カーネル密度推定のプロット
axs[1, 0].plot(theta_support, gaussian_kde(theta_sim10).evaluate(theta_support), color='lightblue', lw=2)
axs[1, 0].plot(theta_support, gamma.pdf(theta_support, a, scale=1/b), color='gray', lw=2)

axs[1, 1].plot(theta_support, gaussian_kde(theta_sim100).evaluate(theta_support), color='lightblue', lw=2)
axs[1, 1].plot(theta_support, gamma.pdf(theta_support, a, scale=1/b), color='gray', lw=2)

axs[1, 2].plot(theta_support, gaussian_kde(theta_sim1000).evaluate(theta_support), color='lightblue', lw=2)
axs[1, 2].plot(theta_support, gamma.pdf(theta_support, a, scale=1/b), color='gray', lw=2)

for ax in axs.flat:
    ax.set(xlim=xlim, ylim=ylim)

plt.tight_layout()
plt.show()

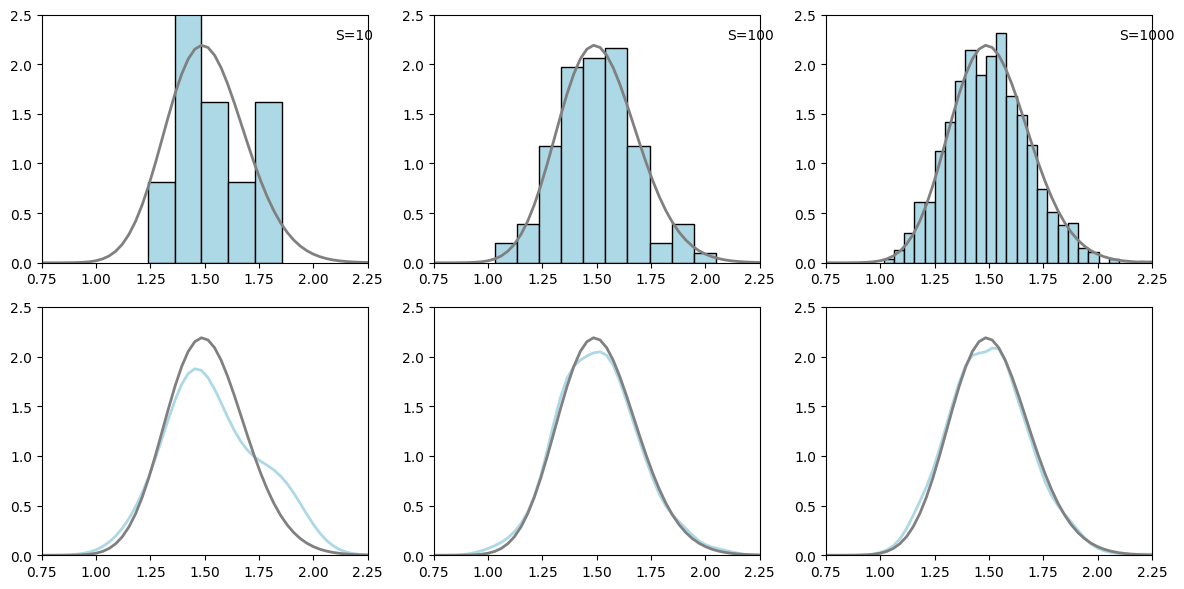
gamma(68,45)分布のモンテカルロ近似のヒストグラムとカーネル密度推定

モンテカルロ標本の作成

# パラメータ設定
np.random.seed(150)
a = 68
b = 45
theta_support = np.linspace(0, 3, 100)

# ガンマ分布からのサンプル
theta_sim10 = np.random.gamma(a, 1/b, 10)
theta_sim100 = np.random.gamma(a, 1/b, 100)
theta_sim1000 = np.random.gamma(a, 1/b, 1000)

ここで事後分布$gamma(68, 45)$からのサンプリングを行なっています。

カーネル密度推定

gaussian_kde(theta_sim10).evaluate(theta_support)

• gaussian_kde は、与えられたデータセットに基づいてカーネル密度推定を行うオブジェクトです。ここではtheta_sim10という$S=10$のモンテカルロ標本を使用しています。
• 生成された KDE オブジェクトに対して evaluate メソッドを使用することで、指定された点（theta_support）での推定密度を計算します。theta_support は、評価したい点の配列であり、このメソッドはそれらの点での密度推定値を返します。

事後平均・特定の確率・95%信用区間のモンテカルロ近似

# 事後平均
post_mean = (a + sy) / (b + n)
# 1.511111111111111

# シミュレーションされた平均
mean_sim10 = np.mean(theta_sim10)
# 1.531433885874973
mean_sim100 = np.mean(theta_sim100)
# 1.5142079692462642
mean_sim1000 = np.mean(theta_sim1000)
# 1.5118584853428694

これは事後平均をモンテカルロ近似しています。事後平均の真の値は1.51です。この結果を見ると、Sが大きくなるにつれて真の値に近づいていることが分かると思います。

# 累積分布関数とシミュレーションによる近似
pgamma_175 = gamma.cdf(1.75, a + sy, scale=1/(b + n))
# 0.8998285727518657
mean_sim10_lt_175 = np.mean(theta_sim10 < 1.75)
# 0.8
mean_sim100_lt_175 = np.mean(theta_sim100 < 1.75)
# 0.88
mean_sim1000_lt_175 = np.mean(theta_sim1000 < 1.75)
# 0.894

こちらは$P(\theta < 1.75)$をモンテカルロ近似しています。こちらもSが大きくなるにつれて真の値に近づいています。

# 95% 信頼区間とシミュレーションによる近似
ci_95 = gamma.ppf([0.025, 0.975], a + sy, scale=1/(b + n))
# [1.17343691, 1.89083626]
ci_sim10_95 = np.quantile(theta_sim10, [0.025, 0.975])
# [1.28744259, 1.87249113]
ci_sim100_95 = np.quantile(theta_sim100, [0.025, 0.975])
# [1.15152734, 1.87443595]
ci_sim1000_95 = np.quantile(theta_sim1000, [0.025, 0.975])
# [1.17546797, 1.88494668]

こちらは95%信用区間をモンテカルロ近似しています。こちらもSが大きくなるにつれて真の95信用区間に近づいていきます。

モンテカルロ標本のサンプルサイズの関数としての事後平均、確率$Pr(\theta < 1.75 | y_1, \dots y_n)$,97.5%事後分位点の収束の様子

書籍の図4.2ではガンマ分布$gamma(68, 45)$からのサイズ$S=1000$のサンプルから累積的に計算した推定値に基づく、モンテカルロ推定の真値への収束をグラフで示しています。
Pythonでの実装は以下のとおりです。

# プロット設定
plt.figure(figsize=(15, 3.5))

# パラメータ設定
np.random.seed(40)
a = 2
b = 1
sy = 66
n = 44
nsim = 1000

# ガンマ分布からのサンプル
theta_sim = np.random.gamma(a + sy, 1/(b + n), nsim)

# 累積平均、分散、CDF、97.5%分位数
cmean = np.cumsum(theta_sim) / np.arange(1, nsim + 1)
cvar = np.cumsum(theta_sim ** 2) / np.arange(1, nsim + 1) - cmean ** 2
ccdf = np.cumsum(theta_sim < 1.75) / np.arange(1, nsim + 1)
cq = np.array([np.quantile(theta_sim[:j], 0.975) for j in range(1, nsim + 1)])

# サブプロットの選択
sseq = np.concatenate([[1], np.arange(1, 101) * (nsim / 100)])

# 累積平均、CDF、97.5%分位数の計算（整数インデックス用に調整）
cmean_selected = cmean[sseq.astype(int) - 1]
ccdf_selected = ccdf[sseq.astype(int) - 1]
cq_selected = cq[sseq.astype(int) - 1]

# 累積平均のプロット
plt.subplot(1, 3, 1)
plt.plot(sseq, cmean_selected, 'black')
plt.axhline(y=(a + sy) / (b + n), color='gray', lw=2)
plt.xlabel('sample size')
plt.ylabel('Cumulative Mean')

# 累積CDFのプロット
plt.subplot(1, 3, 2)
plt.plot(sseq, ccdf_selected, 'black')
plt.axhline(y=gamma.cdf(1.75, a + sy, scale=1/(b + n)), color='gray', lw=2)
plt.xlabel('sample size')
plt.ylabel('Cumulative CDF at 1.75')

# 累積97.5%分位数のプロット
plt.subplot(1, 3, 3)
plt.plot(sseq, cq_selected, 'black')
plt.axhline(y=gamma.ppf(0.975, a + sy, scale=1/(b + n)), color='gray', lw=2)
plt.xlabel('sample size')
plt.ylabel('Cumulative CDF at 97.5%')

plt.tight_layout()
plt.show()

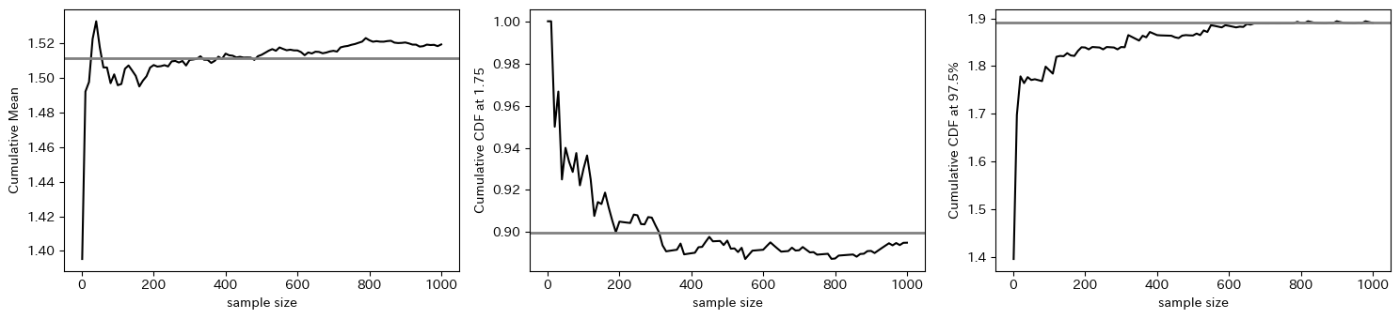
モンテカルロ標本のサンプルサイズの関数としての事後平均

対数オッズの事前分布と事後分布のモンテカルロ近似

1988年の総合的社会調査によると、回答者の54%がプロテスタントで、非プロテスタントは少数派でした。調査では、公立学校での経典読書を州や地方政府が要求することを禁じる最高裁判所の判決についての意見を尋ねました。宗教的少数派860人中441人（51%）がこの判決に賛成し、プロテスタント1011人中353人（35%）が賛成しました。そこで、図4.3では対数オッズを$\gamma = log \frac{\theta}{1-\theta}$をモンテカルロ標本をもとに作成し、プロットしました。
Pythonでの実装は以下のとおりです。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import beta
import seaborn as sns

# パラメータ設定
np.random.seed(1)
a = 1
b = 1
n0 = 860 - 441
n1 = 441

# ベータ分布からのサンプリング
theta_prior_sim = beta.rvs(a, b, size=10000)
gamma_prior_sim = np.log(theta_prior_sim / (1 - theta_prior_sim))

theta_post_sim = beta.rvs(a + n1, b + n0, size=10000)
gamma_post_sim = np.log(theta_post_sim / (1 - theta_post_sim))

# 密度推定のプロット
plt.figure(figsize=(14, 3.5))

# 事前分布
plt.subplot(1, 2, 1)
sns.kdeplot(gamma_prior_sim, color="gray")
plt.xlim(-5, 5)
plt.xlabel(r'$\gamma$')
plt.ylabel(r'$p(\gamma)$')
plt.title("Prior Distribution")

# 事後分布
plt.subplot(1, 2, 2)
sns.kdeplot(gamma_prior_sim, color="gray")
sns.kdeplot(gamma_post_sim, color="black")
plt.xlim(-5, 5)
plt.xlabel(r'$\gamma$')
plt.ylabel(r'$p(\gamma|y_1,\ldots,y_n)$')
plt.title("Posterior Distribution")

plt.show()

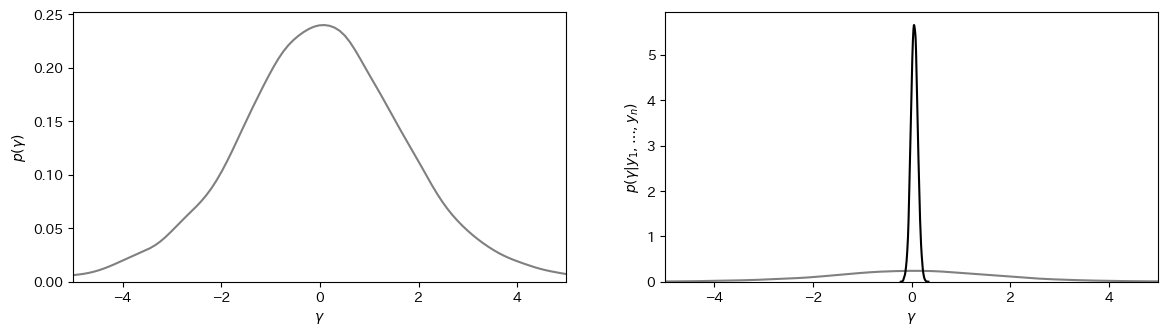
対数オッズの事前分布と事後分布のモンテカルロ近似

$\gamma = \frac{\theta_1}{\theta_2}$の事後予測分布のモンテカルロ近似

出生率の例における事前分布とデータに基づく、学歴に関する二つのグループに対する事後分布は次で与えられます。

$$\{\theta_1 | y_{1,1} \dots y_{n_1,1}\} = gamma(291,112)・・・・学士号を持っていない女性 \\ \{\theta_2 | y_{1,2} \dots y_{n_2,2}\} = gamma(68, 45) ・・・・学士号を持っている女性$$

この事後分布から作成したモンテカルロ標本を用いると、

$$Pr(\theta_1 > \theta_2|\Sigma^{111}_{i=1}Y_{i,1}=217,\Sigma^{44}_{i=1}Y_{i,2}=66) = \frac{1}{S}\Sigma^{S}_{s=1} 1(\theta^{(s)}_{1} > \theta^{(s)}_{2})$$

のように近似することができます。Pythonで実装すると以下のようになります。

# パラメータ設定
a = 2
b = 1
n1 = 111
s1 = 217
n2 = 44
s2 = 66

# モンテカルロシミュレーション
th1_mc = np.random.gamma(a + s1, 1/(b + n1), 100000)
th2_mc = np.random.gamma(a + s2, 1/(b + n2), 100000)

mean_th1_gt_th2 = np.mean(th1_mc > th2_mc)
print(mean_th1_gt_th2)
# 0.97236

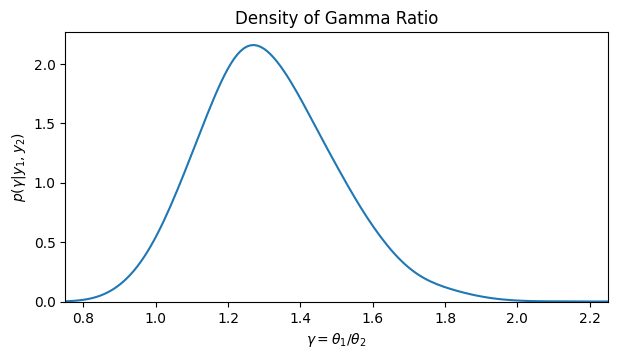
さらに、二つのグループの比に興味がある場合は、$\{\theta^{(1)}_{1}/\theta^{(2)}_{2} \dots \theta^{(S)}_{1}/\theta^{(S)}_{2}\}$の経験分布を用いることで近似することができます。図4.4ではその比のモンテカルロ標本をプロットしています。Pythonでの実装は以下のとおりです。

import matplotlib.pyplot as plt
from scipy.stats import gamma

# パラメータ設定
np.random.seed(1)
a = 2
b = 1
sy1 = 217
n1 = 111
sy2 = 66
n2 = 44

# ガンマ分布からのサンプル
theta1_mc = gamma.rvs(a + sy1, scale=1/(b + n1), size=10000)
theta2_mc = gamma.rvs(a + sy2, scale=1/(b + n2), size=10000)

# ガンマ比率の密度プロット
plt.figure(figsize=(7, 3.5))
sns.kdeplot(theta1_mc / theta2_mc, bw_adjust=2)
plt.xlim(0.75, 2.25)
plt.xlabel(r'$\gamma = \theta_1 / \theta_2$')
plt.ylabel(r'$p(\gamma|y_1, y_2)$')
plt.title("Density of Gamma Ratio")
plt.show()

$\gamma=\frac{\theta_1}{\theta_2}$の事後予測分布のモンテカルロ近似

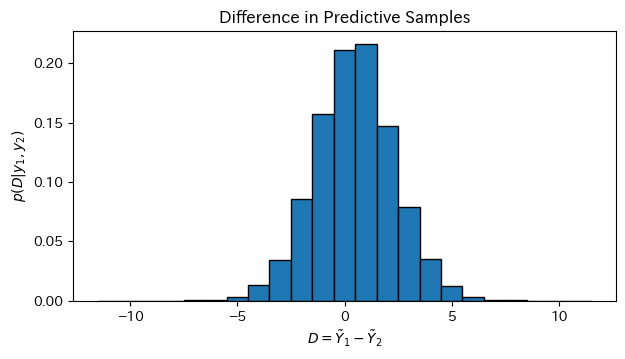
二つの教育に関する各母集団のそれぞれからランダムにサンプルされた二人の女性の子供の数の差$D=\tilde{Y_1}-\tilde{Y_2}$の事後予測分布

図4.5は学士号を持つ女性とそうでない女性の子供の数の差$D=( \tilde{Y_1}-\tilde{Y_2})$の事後予測分布です。Pythonで再現すると以下のようになります。

import matplotlib.pyplot as plt
from scipy.stats import gamma, poisson

# パラメータ設定
np.random.seed(1)
a = 2
b = 1
sy1 = 217
n1 = 111
sy2 = 66
n2 = 44

# ガンマ分布からのサンプル
theta1_mc = gamma.rvs(a + sy1, scale=1/(b + n1), size=10000)
theta2_mc = gamma.rvs(a + sy2, scale=1/(b + n2), size=10000)

# ポアソン分布からのサンプル
y1_mc = poisson.rvs(theta1_mc)
y2_mc = poisson.rvs(theta2_mc)


# y1とy2の差のプロット
diff_mc = y1_mc - y2_mc
ds = np.arange(-11, 12)
diff_table = np.histogram(diff_mc, bins=np.arange(-11.5, 12.5, 1), density=True)[0]

plt.figure(figsize=(7, 3.5))
plt.bar(ds, diff_table, width=1, edgecolor='black')
plt.xlabel(r'$D = \tilde{Y}_1 - \tilde{Y}_2$')
plt.ylabel(r'$p(D|y_1, y_2)$')
plt.title("Difference in Predictive Samples")
plt.show()

$D=\tilde{Y_1}-\tilde{Y_2}$

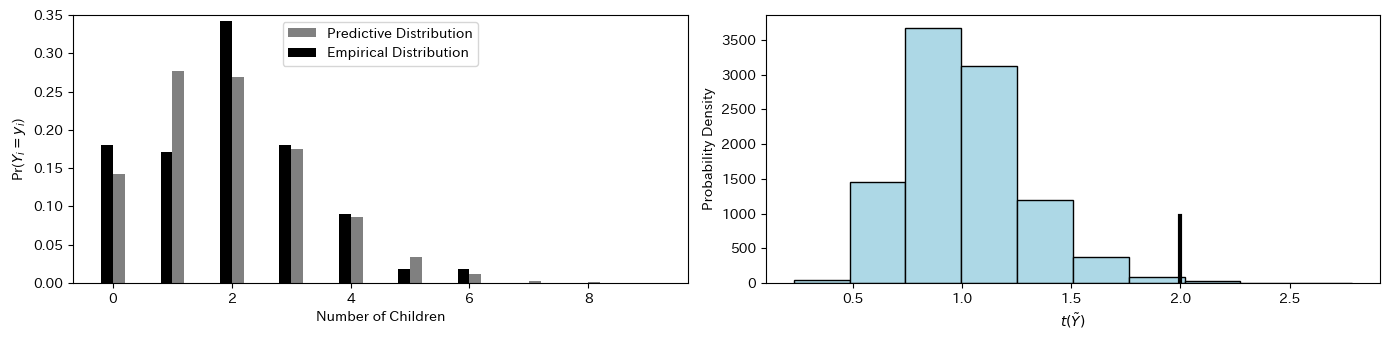
モデル適合性の評価

図4.6の左図には学士号を持っていない女性の子供の数の経験分布と事後予測分布が示されています。右図はサンプルサイズ$n=111$のデータセットにおいて経験オッズの事後予測分布を表しています。観測されたオッズは短い縦線で表しています。Pythonの実装は以下のとおりです。

import numpy as np
from scipy.stats import gamma, poisson, nbinom

# パラメータ設定
np.random.seed(1)
a = 2
b = 1

# gssデータセットから y1 のデータを抽出
y1 = gss_data[(gss_data['FEMALE'] == 1) & (gss_data['YEAR'] >= 1990) &
              (gss_data['AGE'] == 40) & (gss_data['DEGREE'] < 3)]['CHILDS']
y1 = y1.dropna()

# モンテカルロシミュレーション
t_mc = []
for s in range(10000):
    theta1 = gamma.rvs(a + y1.sum(), scale=1/(b + len(y1)))
    y1_mc = poisson.rvs(theta1, size=len(y1))
    t_mc.append(np.sum(y1_mc == 2) / np.sum(y1_mc == 1))

# 実際の観測比
t_obs = np.sum(y1 == 2) / np.sum(y1 == 1)

# プロット設定
plt.figure(figsize=(14, 3.5))

#  事後予測分布
ecdf_mc = nbinom.pmf(np.arange(10), a + y1.sum(), (b + len(y1)) / (b + len(y1) + 1))

# 経験分布
total_count = y1.value_counts().sort_index().values.sum()
proportions = y1.value_counts().sort_index().values / total_count
extended_proportions = np.append(proportions, [np.nan, np.nan, np.nan])

# 1つ目のプロット（経験分布と事後予測分布）
plt.subplot(1, 2, 1)
plt.bar(np.arange(10) + 0.1, ecdf_mc, width=0.2, color='gray', label='Predictive Distribution')
plt.bar(np.arange(10) - 0.1, extended_proportions, width=0.2, color='black', label='Empirical Distribution')
plt.xlabel('Number of Children')
plt.ylabel('Pr($Y_i = y_i$)')
plt.ylim(0, 0.35)
plt.legend()

# 2つ目のプロット
plt.subplot(1, 2, 2)
plt.hist(t_mc, color='lightblue', edgecolor='black')
plt.axvline(t_obs, 0, 0.25, color='black', linewidth=3)
plt.xlabel(r'$t(\tilde{Y})$')
plt.ylabel('Probability Density')

plt.tight_layout()
plt.show()

モデル適合性の評価

最後に

本記事では、ベイズ統計学における強力なツールであるモンテカルロ法について、Pythonを用いた実装と共に説明してきました。単純な事後分布の推定から、複雑な関数の評価、さらにはモデルの適合性評価まで、モンテカルロ法がさまざまな用途で利用できることがわかったと思います。次回は第5章「正規モデル」について解説します。