Zenn
DMM Data BlogPublicationへの投稿
🎉

Pythonで再現する標準ベイズ統計学3章

stochi
2024/08/03に公開
Python
データ分析
統計学
ベイズ統計学
tech

はじめに

本記事では、Peter D. Hoffの著書「標準ベイズ統計学」第3章の内容を、Pythonを用いて実装・解説します。

3章：二項モデルとポアソンモデル

第3章では、ベイズ統計学の基礎となる二つの重要なモデルに焦点を当てています：

  1. 二項モデル
  2. ポアソンモデル

これらのモデルは、単一のパラメータで定義される比較的シンプルな構造を持ちながら、実世界の多様な現象を記述するのに適しています。本章では、以下のベイズ統計学の概念を：

  • 共役事前分布
  • ベイズ推定による予測分布
  • 信用区間の解釈

これらの概念をPythonで実装していきます。

\thetaの関数としての標本確率と事後分布

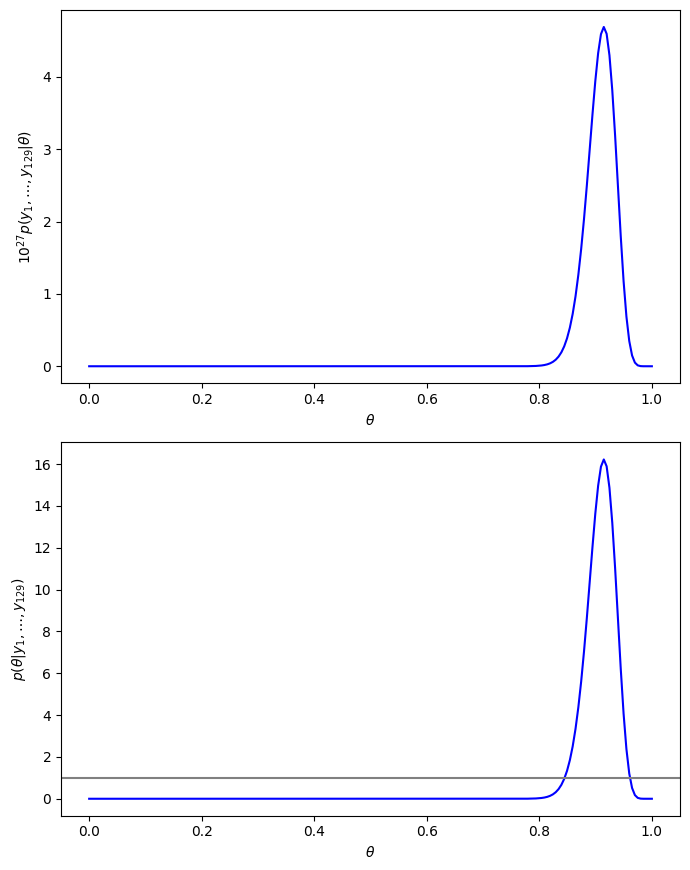
図3.1が掲載されている3.1節では二項モデルを幸福度データを利用し説明しています。幸福度データの詳細は以下のとおりです。

  • 65歳以上の女性に総じて幸せかどうかを質問した調査結果のデータ
  • 回答者が129人
  • 総じて幸せと回答した人が118人(91%)
  • 総じて幸せと回答しなかった人が11人(9%)

ある\thetaが与えられたもとでのこれらのデータの確率は

p(y_1 \dots y_{129}|\theta) = \theta^{118}(1-\theta)^{11}

となります。図3.1の上段の図はこの確率を\thetaの関数とみて図示したものです。
次に、一様事前分布を利用した二項モデルの事後分布（べータ分布）は次の通りです。

p(\theta | y_{1}, \ldots, y_{129}) = \frac{\Gamma{(119)}\Gamma{(12)}}{\Gamma{(131)}} \theta^{119-1}(1-\theta)^{12-1}

これをプロットしたのが図3.1の下段の図となります。
Pythonで実装すると以下のようになります。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta

# CSVファイルの読み込み
file_path = '/content/gss.csv'
gss_data = pd.read_csv(file_path)

# 条件に合致するデータの抽出
y = gss_data[(gss_data['YEAR'] == 1998) & (gss_data['AGE'] >= 65) & (gss_data['FEMALE'] == 1)]['HAPUNHAP']
y[y > 4] = np.nan
y[y <= 2] = 1
y[y > 2] = 0
y = y.dropna()

sy = np.sum(y)
n = len(y)

# プロット設定
plt.figure(figsize=(7, 8.8))

# 1つ目のプロット
theta = np.linspace(0, 1, 200)
plt.subplot(2, 1, 1)
plt.plot(theta, 10**27 * theta**sy * (1 - theta)**(n - sy), 'b-')
plt.xlabel(r'$\theta$')
plt.ylabel(r'$10^{27}p(y_1,\ldots,y_{129}|\theta)$')

# 2つ目のプロット
plt.subplot(2, 1, 2)
plt.plot(theta, beta.pdf(theta, sy + 1, n - sy + 1), 'b-')
plt.axhline(y=1, color='gray')
plt.xlabel(r'$\theta$')
plt.ylabel(r'$p(\theta|y_1,\ldots,y_{129})$')

plt.tight_layout()
plt.show()


\thetaの関数としての標本確率（上段）と事後分布（下段）

以下でPythonプログラムの解説を行います。ただし、前回の記事で紹介したことに関する説明はしません。

条件に合致するデータの抽出

y = gss_data[(gss_data['YEAR'] == 1998) & (gss_data['AGE'] >= 65) & (gss_data['FEMALE'] == 1)]['HAPUNHAP']
  • この行では、gss_data DataFrameから、1998年に行われた調査で、65歳以上の女性のデータをフィルタリングします。
    • 特にHAPUNHAP列（恐らく幸福度を表す何らかの指標）を抽出して、yという新しい変数に格納します。

データのクレンジングと変換

y[y > 4] = np.nan
y[y <= 2] = 1
y[y > 2] = 0
  • この部分で、y内の値に基づいてデータをクリーニングしています。
  • yの値が4より大きい場合は、そのデータ点を欠損値（np.nan）に置換します。
  • yの値が2以下の場合は、その値を1に置換します。（総じて幸福であると答えた女性）
  • yの値が2より大きい場合は、その値を0に置換します。（総じて幸福であるとは答えていない女性）

欠損値の除去

y = y.dropna()
  • dropna()メソッドを使って、yからすべての欠損値を削除します。

データの集約

sy = np.sum(y)
n = len(y)
  • np.sum(y)は、y内の値の合計を計算します。この場合、yは0と1の値しか持たないので、これは1の数、つまり女性の中で総じて幸福である（2以下）と答えた人数を数えています。
  • len(y)はデータの総数を返します。

1つ目のプロット

plt.plot(theta, 10**27 * theta**sy * (1 - theta)**(n - sy), 'b-')

ここで、

\theta^{118}(1-\theta)^{11}

の実装を行い、plt.plotでプロットしています。
観測データy_{1} \dots y_{129}が与えられたときの\thetaの尤度を10^{27}倍して視覚化しやすく調整しています。

2つ目のプロット

plt.plot(theta, beta.pdf(theta, sy + 1, n - sy + 1), 'b-')

ここで、

\frac{\Gamma{(119)}\Gamma{(12)}}{\Gamma{(131)}} \theta^{119-1}(1-\theta)^{12-1}

の実装を行い、plt.plotでプロットしています。

標準ベイズ統計学3.1節の最後に事後分布の中央値、期待値、標準偏差を計算しています。Pythonで計算する際には以下のようになります。

ap = sy + 1
bp = n - sy + 1
pmd = (ap - 1) / (ap - 1 + bp - 1)
pmn = ap / (ap + bp)
pvr = pmn * (1 - pmn) / (ap + bp + 1)

pmd # 0.9147286821705426
pmn # 0.9083969465648855
pvr # 0.0006303934396702886

  • ap（alpha parameter）と bp（beta parameter）は、ベータ分布の形状パラメータです。

  • syは女性の中で総じて幸福であると答えた人数、nは試行回数です。

  • モード (pmd):

    • ベータ分布のモード（最も頻繁に発生する値）は、
    \frac{(α - 1)}{(α + β - 2)}

    で計算されます。ここでα > 1 と β > 1 の場合に有効です。

  • 平均 (pmn):

    • ベータ分布の平均は、
    \frac{α}{(α + β)}

    で与えられます。

  • 分散 (pvr):

    • ベータ分布の分散は、
    \frac{αβ}{(α + β)^2 (α + β + 1)}

    で計算されます。

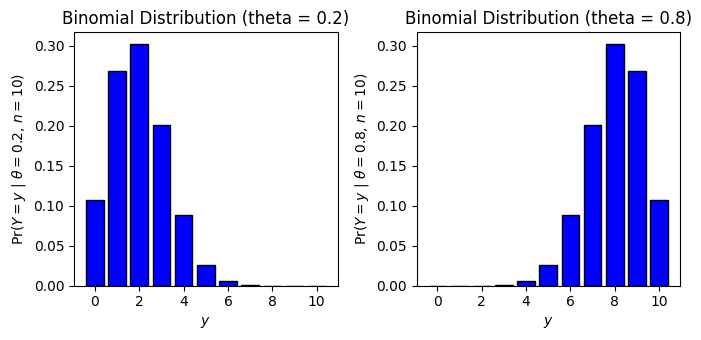
n=10、\theta \in \{0.2,0.8\}の二項分布とn=100、\theta \in \{0.2,0.8\}の二項分布

図3.2, 3.3では異なるnと\thetaの値に対する二項分布のグラフを示しています。
Pythonで実装すると以下のようになります。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import binom

# パラメータ設定
n = 10
theta1 = 0.2
theta2 = 0.8

# xの値の範囲
x = np.arange(0, n + 1)

# プロット設定
plt.figure(figsize=(7, 3.5))

# 1つ目のプロット (theta = 0.2)
plt.subplot(1, 2, 1)
plt.bar(x, binom.pmf(x, n, theta1), color='blue', edgecolor='black')
plt.xlabel(r'$y$')
plt.ylabel(r'Pr($Y=y$ | $\theta=0.2$, $n=10$)')
plt.title('Binomial Distribution (theta = 0.2)')

# 2つ目のプロット (theta = 0.8)
plt.subplot(1, 2, 2)
plt.bar(x, binom.pmf(x, n, theta2), color='blue', edgecolor='black')
plt.xlabel(r'$y$')
plt.ylabel(r'Pr($Y=y$ | $\theta=0.8$, $n=10$)')
plt.title('Binomial Distribution (theta = 0.8)')

plt.tight_layout()
plt.show()


n=10, \theta \in \{0.2,0.8\}の二項分布

# プロット設定
plt.figure(figsize=(7, 3.5))

# パラメータ設定
n = 100
theta1 = 0.2
theta2 = 0.8

# xの値の範囲
x = np.arange(0, n + 1)

# 1つ目のプロット (theta = 0.2)
plt.subplot(1, 2, 1)
plt.bar(x, binom.pmf(x, n, theta1), color='blue', edgecolor='black')
plt.xlabel(r'$y$')
plt.ylabel(r'Pr($Y=y$ | $\theta=0.2$, $n=100$)')
plt.title('Binomial Distribution (theta = 0.2)')

# 2つ目のプロット (theta = 0.8)
plt.subplot(1, 2, 2)
plt.bar(x, binom.pmf(x, n, theta2), color='blue', edgecolor='black')
plt.xlabel(r'$y$')
plt.ylabel(r'Pr($Y=y$ | $\theta=0.8$, $n=100$)')
plt.title('Binomial Distribution (theta = 0.8)')

plt.tight_layout()
plt.show()


n=100, \theta \in \{0.2,0.8\}の二項分布

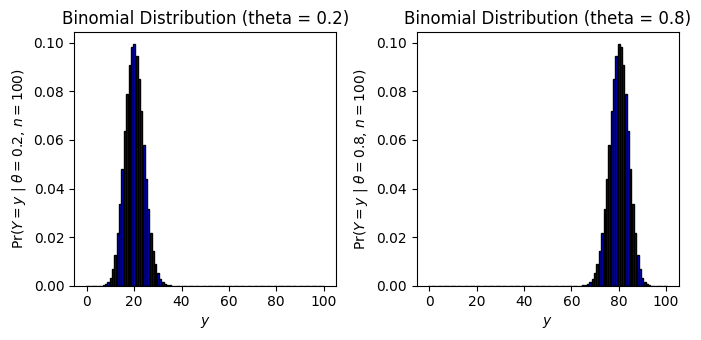
二項分布のプロット

plt.bar(x, binom.pmf(x, n, theta1), color='blue', edgecolor='black')
  • binom.pmf(x, n, theta):
    • ここで使用されているのは、binom.pmf関数です。これは、二項分布の確率質量関数（Probability Mass Function, PMF）を計算するためのものです。
    • n: 試行回数
    • theta: 各試行での成功確率
      この関数は、xで指定された各成功回数に対する確率を計算し、それらの確率値を返します。

その他のプログラムの解説は不要だと思うため、省略します。

二つの異なるサンプルサイズと事前分布のもとでのベータ事後分布

図3.4では二つの異なるサンプルサイズと事前分布のもとでのベータ事後分布をプロットしています。

事前分布に一様分布を用いた場合の事後分布

事前分布に一様分布を用いた事後分布は以下のようになります。

\frac{\Gamma{(n+2)}}{\Gamma{(y+1)\Gamma{(n-y+1)}}} \theta^{(y+1)-1} (1-\theta)^{(n-y+1)-1}

すなわち、一様事前分布を用いた二項モデルの事後分布はbeta(y+1, n-y+1)となります。

ベータ分布を事前分布に用いた場合の事後分布の導出

事前分布にベータ分布beta(a,b)を用いた事後分布は以下の通りです。

beta(a+y, b+n-y)

Pythonでの実装

# プロット設定
plt.figure(figsize=(10, 7))

# theta の範囲
theta = np.linspace(0, 1, 100)

# 各プロットのパラメータ
parameters = [
    {'a': 1, 'b': 1, 'n': 5, 'y': 1},
    {'a': 3, 'b': 2, 'n': 5, 'y': 1},
    {'a': 1, 'b': 1, 'n': 100, 'y': 20},
    {'a': 3, 'b': 2, 'n': 100, 'y': 20}
]

# 各プロットの作成
for i, params in enumerate(parameters, 1):
    a, b, n, y = params.values()
    plt.subplot(2, 2, i)
    plt.plot(theta, beta.pdf(theta, a + y, b + n - y), 'b-', lw=2, label='Posterior')
    plt.plot(theta, beta.pdf(theta, a, b), 'gray', lw=2, label='Prior' if i == 1 else "_nolegend_")
    plt.xlabel(r'$\theta$')
    plt.ylabel(r'$p(\theta|y)$')
    plt.title(f'Beta({a},{b}) prior, n={n}, Σy={y}')
    plt.legend()

plt.tight_layout()
plt.show()


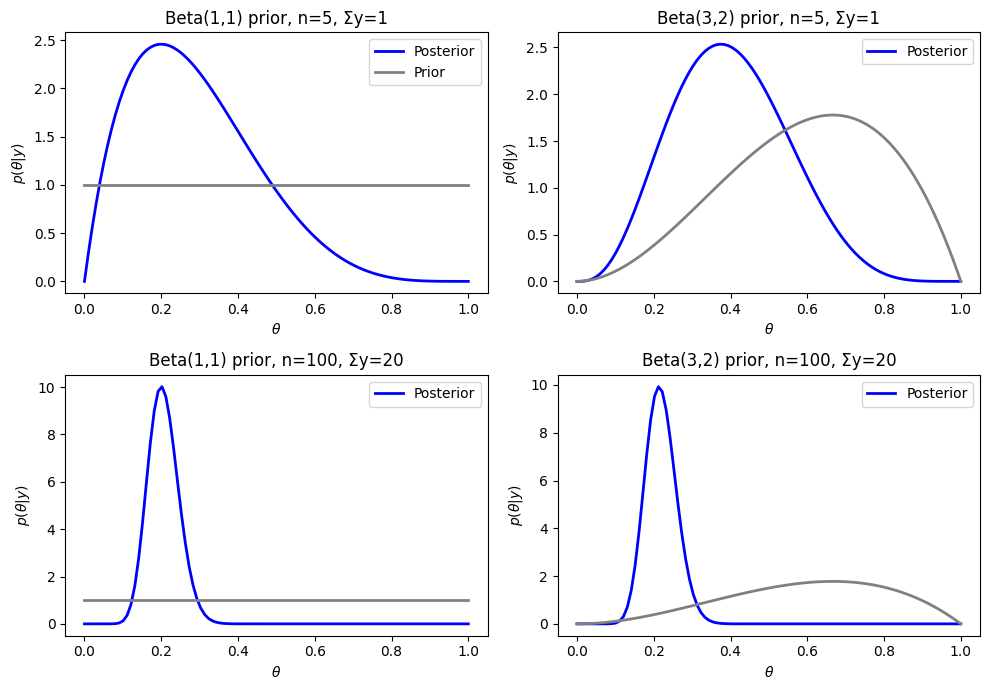
二つの異なるサンプルサイズと事前分布のもとでのベータ事後分布

改めてプログラムに関して説明する必要はないと思うため、解説は省略します。

ベータ事後分布とその分位点にもとづく95%信用区間と確率\alphaを変化させたときの最高事後密度区間

図3.5,3.6が掲載されている節ではベイズ信用区間について解説されています。図3.5は一様事前分布を用いたベータ事後分布の信用区間をプロットしています。
Pythonで実装すると以下のようになります。

# プロット設定
plt.figure(figsize=(7, 3.5))

# パラメータ設定
a = 1
b = 1
n = 10
y = 2

# thetaの範囲
theta_support = np.linspace(0, 1, 100)

# プロット
plt.plot(theta_support, beta.pdf(theta_support, a + y, b + n - y), 'b-', lw=2)
plt.xlabel(r'$\theta$')
plt.ylabel(r'$p(\theta|y)$')

# 信用区間の追加
ci_lower, ci_upper = beta.ppf([0.025, 0.975], a + y, b + n - y)
plt.axvline(x=ci_lower, color='gray', linestyle='--')
plt.axvline(x=ci_upper, color='gray', linestyle='--')

plt.title('Posterior Distribution with 95% Credible Interval')
plt.show()


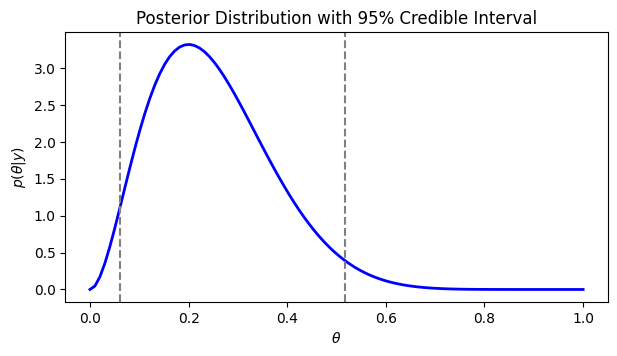
ベータ事後分布とその分位点に基づく95%信用区間（垂直の線）

信用区間の上限と下限

ci_lower, ci_upper = beta.ppf([0.025, 0.975], a + y, b + n - y)

[0.025, 0.975]のように分位点を設定すると、その分位点の値を返すようになっています。その地点でaxvlineを用いて垂直線を描くようにしています。

図3.6は一様事前分布を用いたベータ事後分布のHPD(最高密度領域)をプロットしています。
Pythonで実装すると以下のようになります。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta

def hpd(x, dx, p):
    md = x[dx == np.max(dx)]
    px = dx / np.sum(dx)
    pxs = -np.sort(-px)
    ct = np.min(pxs[np.cumsum(pxs) < p])
    hpdr = [np.min(x[px >= ct]), np.max(x[px >= ct])]
    return {'hpdr': hpdr, 'mode': md}

# パラメータ設定
a = 1
b = 1
n = 10 
y = 2

# theta の範囲を設定
theta_support = np.linspace(0, 1, 5000)

# 事後分布の計算
pth = beta.pdf(theta_support, a+y, b+n-y)

# ソートとcumulative sumの計算
ord = np.argsort(-pth)
xpx = np.column_stack((theta_support[ord], pth[ord]))
xpx = np.column_stack((xpx, np.cumsum(xpx[:, 1]) / np.sum(xpx[:, 1])))

# プロットの設定
plt.figure(figsize=(10, 5))
plt.plot(theta_support, pth, 'b-')
plt.xlabel(r'$\theta$')
plt.ylabel(r'$p(\theta|y)$')

# HPD区間の計算とプロット
for p, color in zip([0.5, 0.75, 0.95], ['0.75', '0.5', '0']):
    tmp = hpd(xpx[:, 0], xpx[:, 1], p)['hpdr']
    # HPDの出力
    print(tmp)
    plt.plot([tmp[0], tmp[0], tmp[1], tmp[1]],
             beta.pdf([0, tmp[0], tmp[1], 0], a+y, b+n-y),
             color=color, lw=2)

# 95% quantile-based interval
tmp = beta.ppf([0.025, 0.975], a+y, b+n-y)
plt.plot([tmp[0], tmp[0], tmp[1], tmp[1]],
         beta.pdf([0, tmp[0], tmp[1], 0], a+y, b+n-y),
         color='0', lw=2, ls='--')

# 凡例の追加
plt.legend(["Posterior", "50% HPD", "75% HPD", "95% HPD", "95% credible interval"],
           loc='upper left', bbox_to_anchor=(0.65, 1))

plt.tight_layout()
plt.show()


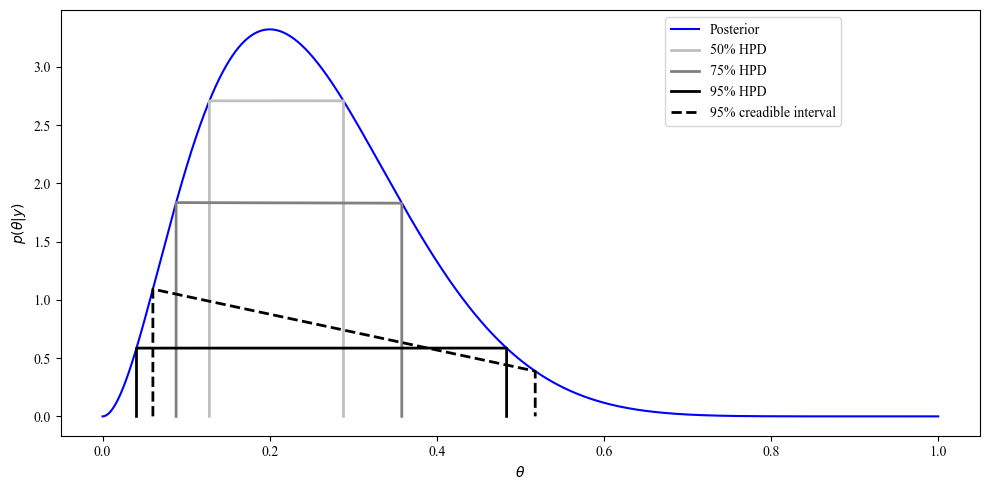
確率\alphaを変化させたときの最高事後密度区間

以下でHPDを計算するプログラムの解説を行います。

def hpd(x, dx, p):
    md = x[dx == np.max(dx)]
    px = dx / np.sum(dx)
    pxs = -np.sort(-px)
    ct = np.min(pxs[np.cumsum(pxs) < p])
    hpdr = [np.min(x[px >= ct]), np.max(x[px >= ct])]
    return {'hpdr': hpdr, 'mode': md}

この関数は以下のパラメータを受け取ります：

x: パラメータの値（この場合、θの値）
dx: 各パラメータ値に対応する確率密度
p: 求めるHPD区間の確率（例：0.95 for 95% HPD）

md = x[dx == np.max(dx)]

確率密度が最大となるx値（モード）を見つけます。

px = dx / np.sum(dx)

確率密度を合計が1になるように正規化します。

pxs = -np.sort(-px)

確率密度を降順にソートします。

ct = np.min(pxs[np.cumsum(pxs) < p])

累積確率がp未満である最小の確率密度を見つけます。これがHPD区間のカットオフ値となります。

hpdr = [np.min(x[px >= ct]), np.max(x[px >= ct])]

カットオフ値以上の確率密度を持つx値の範囲がHPD区間となります。

この関数を用いて、50%HPD, 75%HPD、95%HPDを計算すると、以下のようになります。

50%HPD
# [0.1278255651130226, 0.2882576515303061]
75%HPD
# [0.08801760352070415, 0.35807161432286455]
95%HPD
# [0.04060812162432487, 0.483496699339868]

平均1.83のポアソン分布と1990年代の総合的社会調査から得られた40歳の女性の子供の数の経験分布

図3.7の左図は平均1.83のポアソン分布と1990年代の総合的社会調査から得られた40歳の女性の子供の数の経験分布を表しています。右図は平均1.83のポアソン分布からの10個の独立同一標本の和の分布を表しています。
Pythonで実装すると以下のようになります。

import matplotlib.pyplot as plt
import pandas as pd
from scipy.stats import poisson

# CSVファイルからデータの読み込み
gss_data = pd.read_csv('./csv/gss.csv')

# 条件に合致するデータの抽出
CHILDS = gss_data[(gss_data['FEMALE'] == 1) & (gss_data['YEAR'] >= 1990) &
                  (gss_data['AGE'] == 40) & ~gss_data['DEGREE'].isna()]['CHILDS']
CHILDS = CHILDS[~CHILDS.isna()]

# プロット設定
plt.figure(figsize=(14, 3.5))

# 1つ目のプロット
plt.subplot(1, 2, 1)
# 全体の合計を計算
total_count = CHILDS.value_counts().sort_index().values.sum()
# 各値の割合を計算
proportions = CHILDS.value_counts().sort_index().values / total_count
# 追加の値（NaN）を含む新しい配列を作成
extended_proportions = np.append(proportions, [np.nan, np.nan])
# 新しいSeriesを作成し、インデックスを0から8まで設定
extended_series = pd.Series(extended_proportions, index=[0, 1, 2, 3, 4, 5, 6, 7, 8])
plt.bar(np.arange(9) + 0.1, extended_series, width=0.1, color='gray', label='Empirical Distribution')
plt.bar(np.arange(9) - 0.1, poisson.pmf(np.arange(9), CHILDS.mean()), width=0.1, color='black', label='Poisson Model')
plt.xlabel('Number of Children')
plt.ylabel('Pr($Y_i = y_i$)')
plt.legend()

# 2つ目のプロット（ポアソン分布）
plt.subplot(1, 2, 2)
plt.bar(np.arange(53), poisson.pmf(np.arange(53), 10 * CHILDS.mean()), color='black', lw=3)
plt.xlabel('Number of Children')
plt.ylabel('Pr($\sum Y_i = y | \Theta = 1.83$)')

plt.tight_layout()
plt.show()


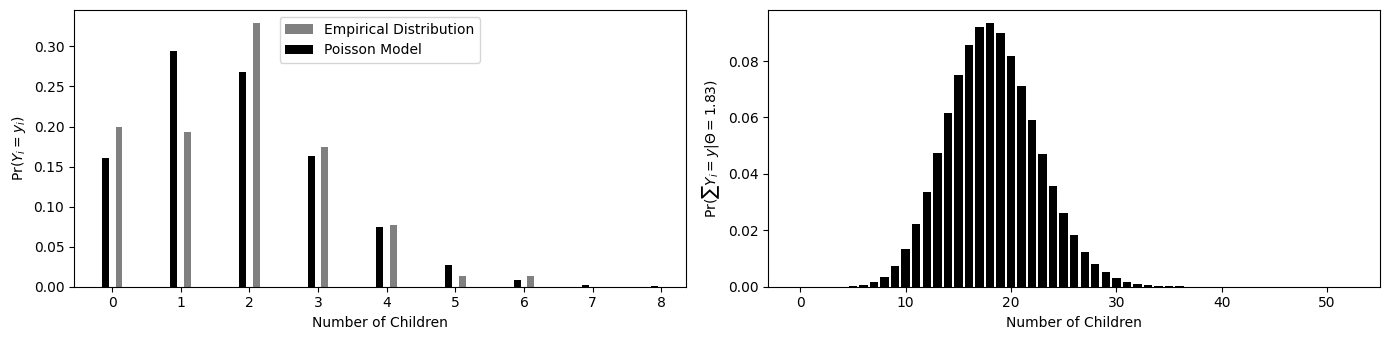
左の図は平均1.83のポアソン分布と1990年代の総合的社会調査から得られた40歳の女性の子供の数の経験分布を表す。右の図は平均1.83のポアソン分布からの10個の独立同一標本の和の分布を表す。

プログラムの解説はこれまでの解説を見れば問題なく理解できるため省略します。

ガンマ分布の密度関数

図3.8はガンマ分布をパラメータを変更してプロットしています。
こちらも特に解説は必要ないと思うため、Pythonの実装だけ載せておきます。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gamma

# プロット設定
plt.figure(figsize=(12, 8))

# theta の範囲
theta = np.linspace(0, 10, 1000)

# 各プロットのパラメータ
parameters = [
    {'a': 1, 'b': 1},
    {'a': 2, 'b': 2},
    {'a': 4, 'b': 4},
    {'a': 2, 'b': 1},
    {'a': 8, 'b': 4},
    {'a': 32, 'b': 16}
]

# サブプロットの作成
fig, axes = plt.subplots(2, 3, figsize=(15, 10))  # 2行3列のサブプロット
axes = axes.flatten()  # 1次元化して扱いやすくする

for ax, params in zip(axes, parameters):
    a, b = params['a'], params['b']
    # スケールパラメータはbの逆数となります
    dist = gamma(a, scale=1/b)
    ax.plot(theta, dist.pdf(theta), 'b-', lw=2)
    ax.set_title(f'Gamma distribution a={a}, b={b}')
    ax.set_xlabel(r'$\theta$')
    ax.set_ylabel(r'$p(\theta)$')

# プロットを見やすくするためのレイアウト調整
plt.tight_layout()
plt.show()


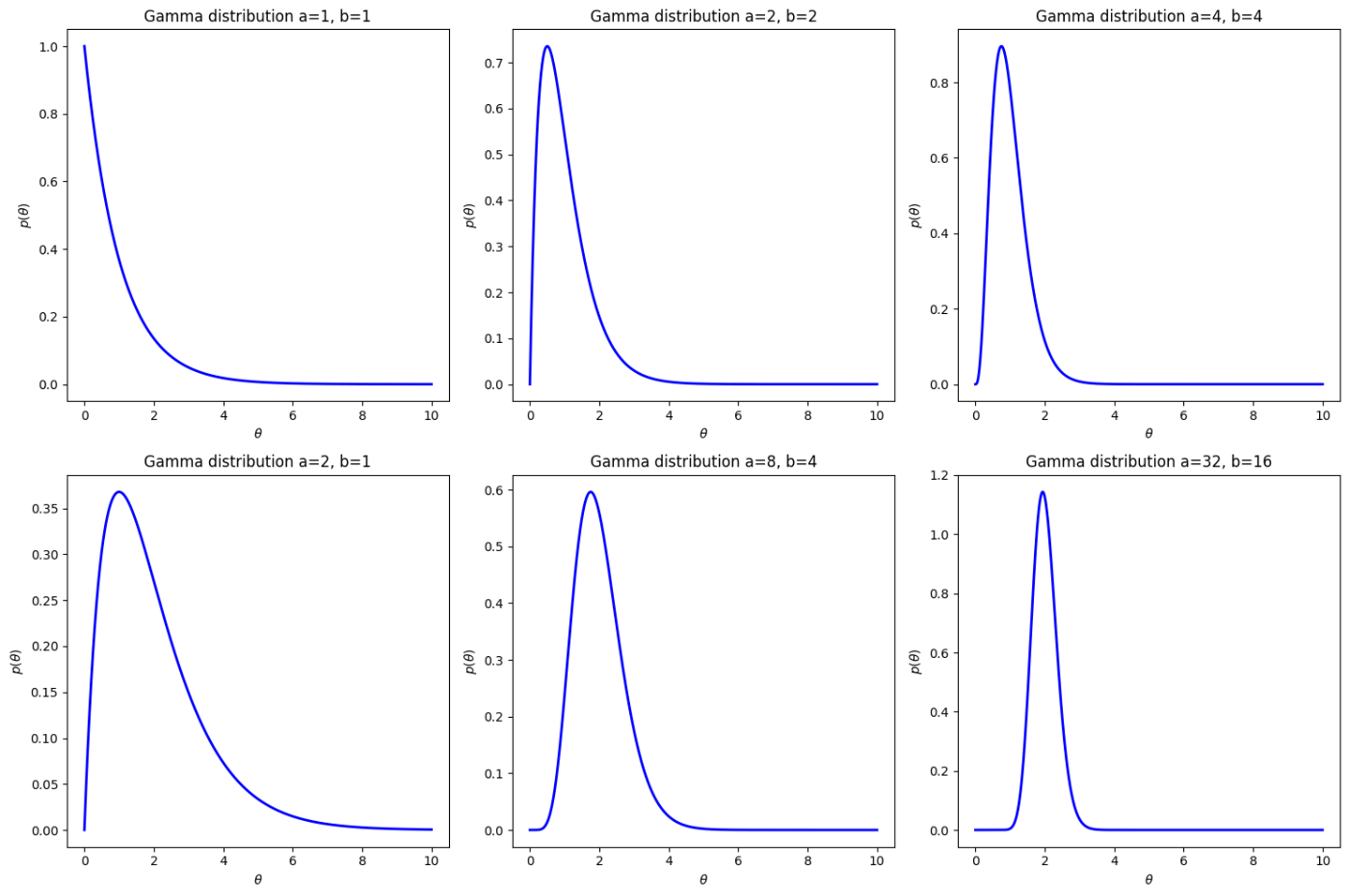
ガンマ分布の密度関数

二つのグループにおける子供の数

1990年代に総合的社会調査が実施され、調査参加時に40歳だった155人の女性を対象に、学歴と子供の数に関するデータが収集されました。図3.9ではこのデータを用いて、学士号を持つ女性と持たない女性の子供の数を比較したグラフが作成されています。
以下がPythonによる実装です。こちらも解説は不要かと思うため省略します。

# プロット設定
plt.figure(figsize=(10, 4))

# データのフィルタリング（'DEGREE'列を使用）
y1 = gss_data[(gss_data['FEMALE'] == 1) & (gss_data['YEAR'] >= 1990) &
              (gss_data['AGE'] == 40) & (gss_data['DEGREE'] < 3)]['CHILDS']
y2 = gss_data[(gss_data['FEMALE'] == 1) & (gss_data['YEAR'] >= 1990) &
              (gss_data['AGE'] == 40) & (gss_data['DEGREE'] >= 3)]['CHILDS']

y1 = y1.dropna()
y2 = y2.dropna()

# 1つ目のプロット（学士未満）
plt.subplot(1, 2, 1)
plt.bar(y1.value_counts().index, y1.value_counts(), color='gray', edgecolor='black', width=0.1)
plt.xlabel('Number of Children')
plt.ylabel('Count')
plt.title("Less than Bachelor's")

# 2つ目のプロット（学士以上）
plt.subplot(1, 2, 2)
plt.bar(y2.value_counts().index, y2.value_counts(), color='black', edgecolor='black', width=0.1)
plt.xlabel('Number of Children')
plt.ylabel('Count')
plt.title("Bachelor's or Higher")

plt.tight_layout()
plt.show()


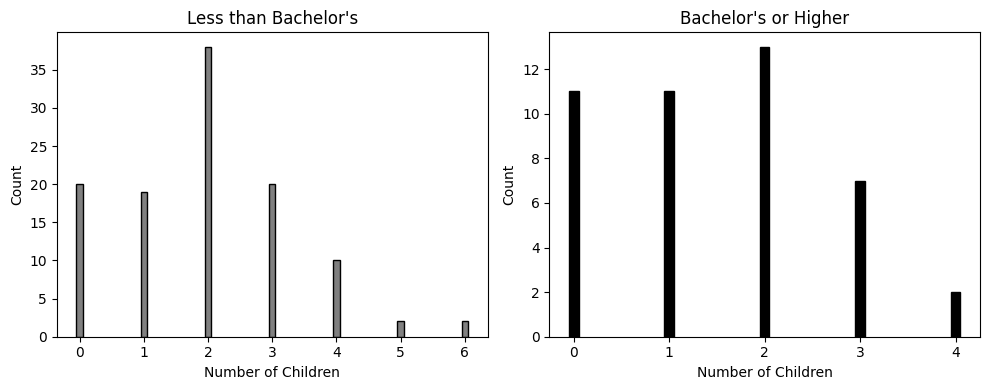
二つのグループにおける子供の数

平均出生率の事後分布および子供の数の事後予測分布

図3.10は、学士号を持っている女性と持っていない女性の子供の数について、ポアソンモデルを用いてモデリングした結果です。この図では、それぞれのグループの事後分布と予測分布がプロットされています。

ポアソンモデルの事後分布

Y_1, \dots Y_n | \theta \sim i.i.d. Poisson(\theta)\\ p(\theta) \sim gamma(a,b)

とすると、事後分布は以下のように導出できます。

p(\theta|y_1, \dots y_n) = p(\theta) × p(y_1 \dots y_n|\theta)/p(y_1 \dots y_n) \\ = \{\theta^{a-1}e^{-b\theta}\}×\{\theta^{\Sigma y_i}e^{-n\theta}\} × c(y_1, \dots y_n, a,b) \\ = \{\theta^{a+\Sigma y_i -1} e^{-(b+n)\theta}\}×c(y_1, \dots y_n, a,b)

このように、事後分布はガンマ分布となります。

ポアソンモデルの予測分布

ポアソンモデルの予測分布は以下のような負の二項分布となります。
（導出の詳細は書籍をご覧ください。）

p(\tilde{y}|y_1 \dots y_n) = \frac{\Gamma{(a + \Sigma y_i + \tilde{y})}}{\Gamma{(\tilde{y}+1)}\Gamma{(a+\Sigma{y_i})}} (\frac{b+n}{b+n+1})^{a+\Sigma{y_i}}(\frac{1}{b+n+1})^{\tilde{y}}

実装

図3.10の左図では以下の三つの分布が、右図では負の二項分布の予測分布がプロットされています。

\{\theta_1, \theta_2\} \sim gamma(a=2, b=1) \\ \theta_1|\{n_1 = 111, \Sigma^{n_1}_{i=1}Y_{i,1}=217\} \sim gamma(2+217, 1+111) \\ \theta_2|\{n_2 = 44, \Sigma^{n_2}_{i=1}Y_{i,2}=66\} \sim gamma(2+66, 1+44) 
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gamma, nbinom

# プロット設定
plt.figure(figsize=(10, 4))

# パラメータ設定
a = 2
b = 1
s1 = np.sum(y1)
n1 = len(y1)
s2 = np.sum(y2)
n2 = len(y2)
xtheta = np.linspace(0, 5, 1000)
y = np.arange(0, 13)

# 1つ目のプロット（ガンマ分布）
plt.subplot(1, 2, 1)
plt.plot(xtheta, gamma.pdf(xtheta, a+s1, scale=1/(b+n1)), color='gray', lw=2, label="Less than bachelor's")
plt.plot(xtheta, gamma.pdf(xtheta, a+s2, scale=1/(b+n2)), color='black', lw=2, label="Bachelor's or higher")
plt.plot(xtheta, gamma.pdf(xtheta, a, scale=1/b), color='black', lw=2, linestyle='--', label="Prior")
plt.xlabel(r'$\theta$')
plt.ylabel(r'$p(\theta|y_1,\ldots,y_n)$')
plt.legend()

# 2つ目のプロット（負の二項分布）
plt.subplot(1, 2, 2)
plt.bar(y - 0.1, nbinom.pmf(y, a+s1, (b+n1)/(b+n1+1)), width=0.2, color='gray', label="Less than bachelor's")
plt.bar(y + 0.1, nbinom.pmf(y, a+s2, (b+n2)/(b+n2+1)), width=0.2, color='black', label="Bachelor's or higher")
plt.xlabel(r'$y_{n+1}$')
plt.ylabel(r'$p(y_{n+1}|y_1,\ldots,y_n)$')
plt.ylim(0, 0.35)
plt.legend()

plt.tight_layout()
plt.show()


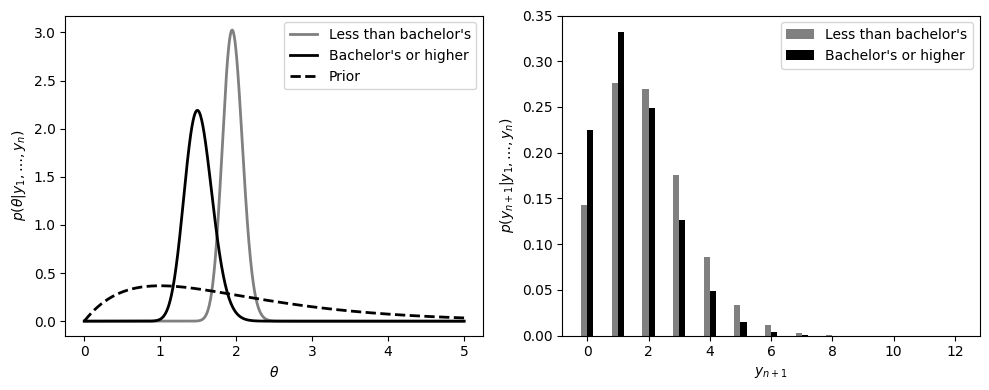
平均出生率の事後分布と子供の数の事後予測分布

事後平均、モード、95%信用区間の計算

以下では学士号をもつ女性の子供の数とそうでない女性の子供の数の事後分布の事後平均、モード、95%信用区間を計算します。

from scipy.stats import gamma, poisson, nbinom

# パラメータ設定
a = 2
b = 1
n1 = 111
s1 = 217
n2 = 44
s2 = 66

# 学士号を持たない女性の子供の数の事後平均、モード、95% CI
post_mean1 = (a + s1) / (b + n1)
post_mode1 = (a + s1 - 1) / (b + n1)
post_ci1 = gamma.ppf([0.025, 0.975], a + s1, scale=1/(b + n1))
print(post_mean1)
# 1.9553571428571428
print(post_mode1)
# 1.9464285714285714
print(post_ci1)
# [1.70494315 2.22267902]

# 学士号を持つ女性の子供の数の事後平均、モード、95% CI
post_mean2 = (a + s2) / (b + n2)
post_mode2 = (a + s2 - 1) / (b + n2)
post_ci2 = gamma.ppf([0.025, 0.975], a + s2, scale=1/(b + n2))
print(post_mean2)
# 1.511111111111111
print(post_mode2)
# 1.488888888888889
print(post_ci2)
# [1.17343691 1.89083626]

両者の比較

以下の計算を行い、比較をしていきます。

Pr(\theta_1 > \theta_2 | \Sigma Y_{i,1}=217, \Sigma Y_{i,2}=66) \\ Pr(\tilde{Y_1} > \tilde{Y_2} | \Sigma Y_{i,1}=217, \Sigma Y_{i,2}=66)\\ Pr(\tilde{Y_1} = \tilde{Y_2} | \Sigma Y_{i,1}=217, \Sigma Y_{i,2}=66) 
# モンテカルロシミュレーション
th1_mc = np.random.gamma(a + s1, 1/(b + n1), 100000)
th2_mc = np.random.gamma(a + s2, 1/(b + n2), 100000)

# 比較
mean_th1_gt_th2 = np.mean(th1_mc > th2_mc)
y1_mc = np.random.poisson(th1_mc)
y2_mc = np.random.poisson(th2_mc)
mean_y1_gt_y2 = np.mean(y1_mc > y2_mc)
mean_y1_ge_y2 = np.mean(y1_mc >= y2_mc)
mean_y1_eq_y2 = np.mean(y1_mc == y2_mc)

# 結果の出力
print(mean_th1_gt_th2)
# 0.97232
print(mean_y1_gt_y2)
# 0.47933
print(mean_y1_eq_y2)
# 0.22046

上記の結果より、Pr(\theta_1 > \theta_2 | \Sigma Y_{i,1}=217, \Sigma Y_{i,2}=66) = 0.97232となっており、学士号を持たない女性の方が子供の数の平均が大きいという結果になります。ただし、図3.10の右図を見ると分かるように、予測分布間に大きな差はありません。また、Pr(\tilde{Y_1} > \tilde{Y_2} | \Sigma Y_{i,1}=217, \Sigma Y_{i,2}=66)=0.47933、Pr(\tilde{Y_1} = \tilde{Y_2} | \Sigma Y_{i,1}=217, \Sigma Y_{i,2}=66)=0.22であることからも、母集団間に差があるとしても、その差が大きいわけではないことが理解できます。

最後に

本記事では、Peter D. Hoffの「標準ベイズ統計学」第3章の内容をPythonで実装し、二項モデルとポアソンモデルを中心に、ベイズ統計学の基本的な概念や手法を説明しました。その中でも特に、事前分布、事後分布、予測分布の概念や、HPD（最高密度領域）などの信用区間の解釈は、データ分析において非常に重要な役割を果たします。次回は第4章の内容に進み、より複雑なモデルや高度な概念について説明していく予定です。

DMM Data Blog
DMM Data BlogPublication

DMM.comに所属するデータ分析関連組織の有志によるテックブログです。データ分析に関する知識・技術を発信します。

Discussion