Zenn
DMM Data BlogPublicationへの投稿
😀

Pythonで再現する標準ベイズ統計学2章

stochi
2024/08/02に公開
Python
データ分析
統計学
ベイズ統計学
tech

はじめに

本記事では、Peter D. Hoff著『A First Course in Bayesian Statistical Methods』（邦訳：「標準ベイズ統計学」）の内容をベースに、ベイズ統計学の基本概念をPythonで実装する方法を紹介します。この連載では、イントロの1章を飛ばし、書籍の2章から始めます。各章で扱う内容を簡潔に解説し、それに対応するPythonコードを提供することで、理論と実践の橋渡しのお手伝いができればと考えています。本記事は、ベイズ統計学に興味がある方、Pythonでデータ分析を行いたい方、そして理論を実践に移したい方々に向けて書いています。ただし、これはあくまで入門的な内容であり、詳細な理論や応用については原著をお読みいただくことをお勧めします。

2章：信念、確率、交換可能性

本章では、ベイズ統計学の基礎となる重要な概念を説明しています。：

  1. 合理的な信念関数の性質
  2. 確率の基本的な性質
  3. 離散型と連続型の確率変数
  4. 確率分布の構造
  5. 独立性と交換可能性の関係

これらの概念は後続の章でより高度な内容を学ぶための基礎となっています。

図2.1 平均が2.1と21のポアソン分布

図2.1が掲載されている2.4.1節では離散型確率変数について説明しています。離散型確率変数の例として二項分布・ポアソン分布が挙げられています。確率変数Yが確率θの二項分布を持つとは、

Pr(Y=y|θ) = \binom{n}{y} θ^y (1-θ)^{n-y}

となることを意味します。また、確率変数Yが平均\thetaのポアソン分布をもつとは以下のようになることを意味します。

P(Y = y|θ) = \frac{\theta^y e^{-\theta}}{y!}

標準ベイズ統計学の図2.1では平均が2.1と21のポアソン分布を描画しています。
pythonで実装すると以下のようになります。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import poisson

# プロット設定
plt.figure(figsize=(7, 3.5))

# 1つ目のプロット (theta = 2.1)
x1 = np.arange(0, 11)
plt.subplot(1, 2, 1)
plt.bar(x1, poisson.pmf(x1, 2.1), color='blue', edgecolor='black')
plt.xlabel(r'$y$')
plt.ylabel(r'$p(y|\theta=2.1)$')
plt.title('Poisson Distribution (theta = 2.1)')

# 2つ目のプロット (theta = 21)
x2 = np.arange(0, 101)
plt.subplot(1, 2, 2)
plt.bar(x2, poisson.pmf(x2, 21), color='blue', edgecolor='black')
plt.xlabel(r'$y$')
plt.ylabel(r'$p(y|\theta=21)$')
plt.title('Poisson Distribution (theta = 21)')

plt.tight_layout()
plt.show()


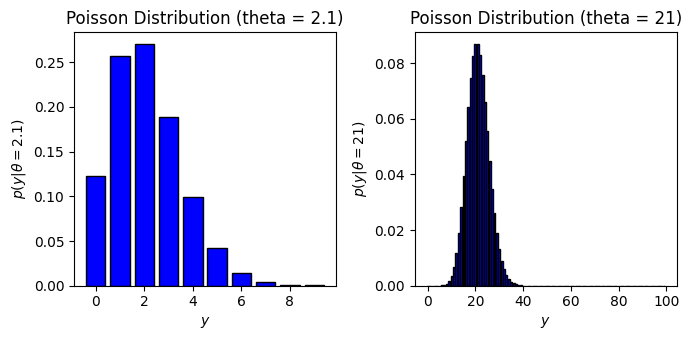
平均が2.1と21のポアソン分布

以下でpythonプログラムの解説を行います。

最初のサブプロット（θ = 2.1の場合）

x1 = np.arange(0, 11)
plt.subplot(1, 2, 1)
plt.bar(x1, poisson.pmf(x1, 2.1), color='blue', edgecolor='black')
plt.xlabel(r'$y$')
plt.ylabel(r'$p(y|\theta=2.1)$')
plt.title('Poisson Distribution (theta = 2.1)')
  • x1 = np.arange(0, 11): 0から10までの整数配列を生成します。
  • plt.subplot(1, 2, 1): 1行2列のグリッドの最初の領域（左側）にサブプロットを配置します。
poisson.pmf(x1, 2.1)

ポアソン分布の確率質量関数（Probability Mass Function, PMF）を計算します。ここでは、ポアソン分布のパラメーター \lambda（平均または期待値）が2.1である場合のPMFを計算しています。

  • 引数:
    • x1: PMFを計算する整数の値の配列。このケースでは np.arange(0, 11) によって0から10までの整数が生成され、それぞれの点でのPMFが計算されます。
    • 2.1: ポアソン分布の平均\lambdaです。
  • 出力
    • poisson.pmf(x1, 21) は、各x1に対する確率の値を持つ配列を返します。この配列は、ポアソン分布に従って、各x1が発生する確率を表します。

2つ目のサブプロット（θ = 21の場合）

x2 = np.arange(0, 101)
plt.subplot(1, 2, 2)
plt.bar(x2, poisson.pmf(x2, 21), color='blue', edgecolor='black')
plt.xlabel(r'$y$')
plt.ylabel(r'$p(y|\theta=21)$')
plt.title('Poisson Distribution (theta = 21)')

一つ目のプロットと同様なので省略します。

図2.2 平均が10.75、標準偏差が0.8の正規分布の累積分布関数と確率密度関数

図2.2が掲載されている2.4.2節では連続型確率変数について説明しています。
具体例として正規分布が紹介されています。正規分布の累積分布関数は以下のとおりです。

Pr(Y \leq y | \mu, \sigma^2) = F(y) =　\int_{-\infty}^{y} \frac{1}{\sqrt{2\pi}\sigma} exp\{-\frac{(y-\mu)^2}{2\sigma^2}\} \, dy

また、確率密度関数は以下のとおりです。

p(y|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} exp\{-\frac{(y-\mu)^2}{2\sigma^2}\}

図2.2では平均10.75、標準偏差が0.8の正規分布の累積分布関数と確率密度関数が描画されています。
pythonで実装すると以下のようになります。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

# プロット設定
plt.figure(figsize=(7, 3.5))

# パラメータ
mu = 10.75
sig = 0.8

# xの値の範囲
x = np.linspace(7.9, 13.9, 500)

# 1つ目のプロット（正規分布の累積分布関数）
plt.subplot(1, 2, 1)
plt.plot(x, norm.cdf(x, mu, sig), 'b-', lw=1)
plt.ylabel(r'$F(y)$')
plt.xlabel(r'$y$')
plt.axhline(y=0, color='gray')
plt.axhline(y=0.5, color='gray')
plt.axhline(y=1, color='gray')
plt.title('Cumulative Distribution Function')

# 2つ目のプロット（正規分布の確率密度関数）
plt.subplot(1, 2, 2)
plt.plot(x, norm.pdf(x, mu, sig), 'b-', lw=1)
plt.ylabel(r'$p(y)$')
plt.xlabel(r'$y$')
plt.axvline(x=mu, color='gray')
plt.title('Probability Density Function')

plt.tight_layout()
plt.show()


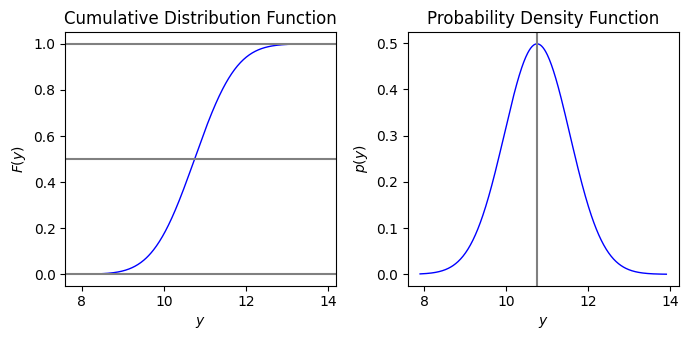
平均が10.75、標準偏差が0.8の正規分布の累積分布関数と確率密度関数

以下でPythonプログラムの解説を行います。ただし、すでに解説した部分に関しては省略します。

正規分布のプロット

norm.cdf(x, mu, sig)
  • norm.cdf(x, mu, sig) は、PythonのSciPyライブラリの一部である正規分布の累積分布関数（Cumulative Distribution Function, CDF）を計算する関数です。ここでの関数は、与えられた平均muと標準偏差sigを持つ正規分布における、特定の値x以下の確率を返します。

図2.3 \mu = 10.75、\sigma=0.8の正規分布と対数正規分布の最頻値、中央値、平均値

図2.3が掲載されている2.4.3節では分布の特徴づけについて解説されています。具体的には最頻値（モード）、中央値（メディアン）、平均値などです。図2.3は\mu = 10.75、\sigma = 0.8の正規分布と対数正規分布の最頻値、中央値、平均値を示しています。
pythonでの実装は以下のとおりです。

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm, lognorm

# 正規分布と対数正規分布のパラメータ
mu = 10.75
sig = 0.8  

# 正規分布のプロット
x1 = np.linspace(7.75, 13.75, 100)
plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
plt.plot(x1, norm.pdf(x1, mu, sig), 'b-', lw=1)
plt.axvline(x=mu, color='gray', linestyle='-')
plt.xlabel(r'$y$')
plt.ylabel(r'$p(y)$')
plt.title('Normal Distribution')

# 対数正規分布のプロット
x2 = np.linspace(0, 300000, 200)
plt.subplot(1, 2, 2)
plt.plot(x2, lognorm.pdf(x2, sig, scale=np.exp(mu)), 'b-', lw=1)
plt.axvline(x=np.exp(mu), color='gray', linestyle='--', label="Mode")  # mode
plt.axvline(x=np.exp(mu - sig**2), color='gray', linestyle='-', label="Median")  # median
plt.axvline(x=np.exp(mu + 0.5 * sig**2), color='gray', linestyle='-.', label="Mean")  # mean
plt.xlabel(r'$y$')
plt.ylabel(r'$p(y)$')
# x軸のメモリを縦に表示
plt.xticks(rotation=90) 
plt.title('Log-Normal Distribution')
plt.legend()

plt.tight_layout()
plt.show()


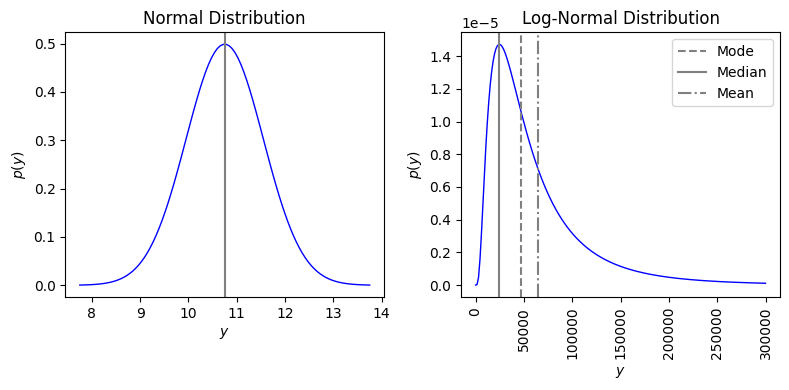
\mu = 10.75、\sigma=0.8の正規分布と対数正規分布の最頻値、中央値、平均値

対数正規分布のプロット

lognorm.pdf(x2, sig, scale=np.exp(mu))
  • lognormal.pdf関数を使用して対数正規分布の確率密度関数（PDF）を求めます。
    • パラメータ
      • x2: 密度を計算したい変数の値を表します。
      • sig:この形状パラメーターは、変数の対数の基となる正規分布の標準偏差を示します。
      • scale=np.exp(mu):このスケールパラメーターは分布のスケールを調整しています。

最後に

本記事では、Peter D. Hoffの「標準ベイズ統計学」第2章をPythonで実装する方法を紹介しました。ポアソン分布、正規分布、対数正規分布といった基本的な確率分布の概念を、Pythonを用いて可視化しました。次回は、第3章「二項モデルとポアソンモデル」の内容を説明します。ここでは、より実践的なモデリング手法を学び、Pythonでの実装を通じて理解を深めていきます。

DMM Data Blog
DMM Data BlogPublication

DMM.comに所属するデータ分析関連組織の有志によるテックブログです。データ分析に関する知識・技術を発信します。

Discussion