Pythonで再現する標準ベイズ統計学11章

はじめに

本記事では標準ベイズ統計学の11章で掲載されている図表やモデルをPythonで実装する方法に関して説明します。

11章：線形・一般化線形混合効果モデル

標準ベイズ統計学の11章では、前章で学んだ基本的な階層モデルの考え方を発展させ、今回は変数間の関係性が集団ごとにどのように変化するかを説明しています。具体的には、集団内のデータの挙動を記述する回帰モデルと、集団間での回帰係数の違いを表現する多変量正規分布を組み合わせるアプローチを紹介しています。これにより、データの持つ複雑な構造をより精密にモデル化することが可能になります。さらに、より柔軟なモデリングを可能にする階層一般化線形モデルについても触れ、その推定方法を解説しています。

得点データに対する最小二乗推定された回帰直線および推定値と集団内サンプルサイズの散布図

図11.1の左図では、100校の回帰直線の最小二乗推定値を示しています。大多数の学校ではSESの増加に伴って数学スコアが上昇する傾向が見られますが、一部の学校では負の関係も見られます。全体の平均を表す黒い線も含まれています。中央の図では、各学校のサンプルサイズと回帰係数の関係を示しています。サンプルサイズが大きい学校は平均に近い回帰係数を持つ傾向があります。右図では、サンプルサイズの小さい学校ほど平均から大きく離れた回帰係数を持つ傾向があることを示しています。

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt

# データ
nels_data = pd.read_csv('./csv/nelsSES.csv')

# 学校IDごとにデータを分割
school_ids = nels_data['sch_id'].unique()
m = len(school_ids)

Y = []
X = []
N = []

# 各学校ごとにデータを処理
for school_id in school_ids:
    school_data = nels_data[nels_data['sch_id'] == school_id]
    Y.append(school_data['stu_mathscore'])
    N.append(len(school_data))

    # SES変数の中心化
    xj = school_data['stu_ses'] - school_data['stu_ses'].mean()
    X.append(sm.add_constant(xj))  # 定数項を追加

# OLS回帰モデルのフィット
BETA_LS = []
S2_LS = []

for j in range(m):
    model = sm.OLS(Y[j], X[j])
    results = model.fit()
    BETA_LS.append(results.params)
    S2_LS.append(results.mse_resid)

# 図の作成（
plt.figure(figsize=(15, 5))

# SESの範囲を取得
ses_range = np.linspace(nels_data['stu_ses'].min(), nels_data['stu_ses'].max(), 100)

# 回帰線のプロット
plt.subplot(1, 3, 1)
plt.xlabel("SES")
plt.ylabel("Math Score")

for j in range(m):
    plt.plot(ses_range, ses_range * BETA_LS[j][1] + BETA_LS[j][0], color='gray', alpha=0.5)

BETA_MLS = np.mean(BETA_LS, axis=0)
plt.plot(ses_range, ses_range * BETA_MLS[1] + BETA_MLS[0], color='black', linewidth=2)

# サンプルサイズに対する切片のプロット
plt.subplot(1, 3, 2)
plt.scatter(N, [beta[0] for beta in BETA_LS])
plt.xlabel("Sample Size")
plt.ylabel("Intercept")
plt.axhline(y=BETA_MLS[0], color='black', linewidth=2)

# サンプルサイズに対する傾きのプロット
plt.subplot(1, 3, 3)
plt.scatter(N, [beta[1] for beta in BETA_LS])
plt.xlabel("Sample Size")
plt.ylabel("Slope")
plt.axhline(y=BETA_MLS[1], color='black', linewidth=2)

plt.tight_layout()
plt.show()

正規階層回帰モデルのグラフ構造の表現

図11.2では正規階層回帰モデルのグラフ構造をプロットされています。
プロットする方法について解説しません。プログラムだけ掲載しておきます。

import matplotlib.pyplot as plt

# 図の作成
plt.figure(figsize=(10, 6))

# プロット領域の設定
plt.plot([0, 1], [0, 1], 'w') 
plt.axis('off')

# θ, Σ の配置
plt.text(0.5, 0.9, r'$\theta, \Sigma$', fontsize=14, ha='center')

# 変数の位置とラベルの設定
positions = [0.1, 0.3, 0.7, 0.9]
beta_labels = [r'$\beta_1$', r'$\beta_2$', r'$\beta_{m-1}$', r'$\beta_m$']
y_labels = [r'$Y_1$', r'$Y_2$', r'$Y_{m-1}$', r'$Y_m$']

# β の配置
for x, label in zip(positions, beta_labels):
    plt.text(x, 0.6, label, fontsize=12, ha='center')
plt.text(0.5, 0.6, r'$\ldots$', fontsize=14, ha='center')

# Y の配置
for x, label in zip(positions, y_labels):
    plt.text(x, 0.3, label, fontsize=12, ha='center')
plt.text(0.5, 0.3, r'$\ldots$', fontsize=14, ha='center')

# σ² の配置
plt.text(0.5, 0.1, r'$\sigma^2$', fontsize=12, ha='center')

# θ, Σ から β への線
for x in positions:
    plt.plot([0.5, x], [0.85, 0.65], 'k-', lw=0.5)

# β から Y への線
for x in positions:
    plt.plot([x, x], [0.55, 0.35], 'k-', lw=0.5)

# σ² から Y への線
for x in positions:
    plt.plot([0.5, x], [0.15, 0.25], 'k-', lw=0.5)

plt.tight_layout()
plt.show()

SESと試験スコアの関係性

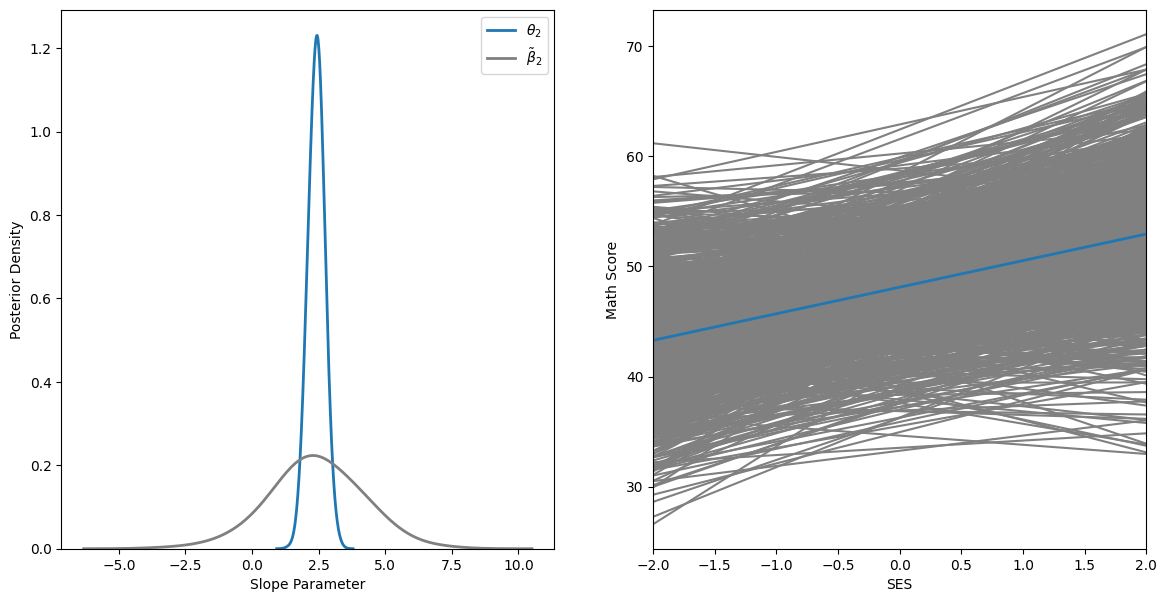
図11.3は、社会経済的地位（SES）と数学スコアの関係を分析した階層モデルの結果を示す図です。左図では、ランダムに抽出された学校の期待される傾き$θ_2$の事後分布と、個別の学校の傾きの事後予測分布$\tilde{\beta}_2$が示されています。$θ_2$の分布は正の値に集中しており、これは学校レベルの傾きの母集団平均が正であることを示唆しています。一方、$\tilde{\beta}_2$の分布はより広がりを持ち、個々の学校の傾きにはより大きな変動があることを表しています。
右図では、100校それぞれの回帰直線の事後期待値をプロットしており、全体の平均を表す青い線も含まれています。この図は、階層モデルがどのようにグループ間で情報を共有し、極端な回帰直線をグループ全体の平均に向けて調整しているかを視覚的に示しています。図11.1の左図と比較すると、情報共有により、ほとんどの傾きが正になっていることがわかります。
この図は、階層モデルの強力さと柔軟性を明確に示しています。個々の学校のデータだけでなく、全体の傾向を考慮することで、より安定した推定が可能になることを表現しています。また、母集団パラメータ（$θ_2$）の推定と個別の学校の予測（$\tilde{\beta}_2$）の違いを明確に示すことで、階層モデルの解釈の重要性も強調しています。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import wishart, multivariate_normal, gamma
import seaborn as sns
import japanize_matplotlib

# 多変量正規分布の関数
def rmvnorm(n, mu, Sigma):
    return multivariate_normal.rvs(mean=mu, cov=Sigma, size=n)

# ウィシャート分布の関数
def rwish(n, nu0, S0):
    return wishart.rvs(df=nu0, scale=S0, size=n)

# データの読み込み
nels_data = pd.read_csv('./csv/nelsSES.csv')

# データの準備
school_ids = nels_data['sch_id'].unique()
m = len(school_ids)
Y = []
X = []
N = []

for school_id in school_ids:
    school_data = nels_data[nels_data['sch_id'] == school_id]
    Y.append(school_data['stu_mathscore'].to_numpy())
    N.append(len(school_data))
    xj = school_data['stu_ses'] - school_data['stu_ses'].mean()
    X.append(np.column_stack((np.ones(len(school_data)), xj)))

# OLS回帰
BETA_LS = np.array([np.linalg.lstsq(X[j], Y[j], rcond=None)[0] for j in range(m)])
S2_LS = np.array([np.var(Y[j] - X[j] @ BETA_LS[j]) for j in range(m)])

# パラメータの設定
p = X[0].shape[1]
theta = mu0 = BETA_LS.mean(axis=0)
nu0 = 1
s2 = s20 = S2_LS.mean()
eta0 = p + 2
Sigma = S0 = L0 = np.cov(BETA_LS.T)
BETA = BETA_LS.copy()
iL0 = np.linalg.inv(L0)
iSigma = np.linalg.inv(Sigma)

# MCMCループ
np.random.seed(1)
S2_b = []
THETA_b = []
SIGMA_PS = []
BETA_pp = []

for s in range(10000):
    # beta_jの更新
    for j in range(m):
        Vj = np.linalg.inv(iSigma + 1/s2 * X[j].T @ X[j])
        Ej = Vj @ (iSigma @ theta + 1/s2 * X[j].T @ Y[j])
        BETA[j] = rmvnorm(1, Ej, Vj)
    
    # thetaの更新
    Lm = np.linalg.inv(iL0 + m * iSigma)
    mum = Lm @ (iL0 @ mu0 + iSigma @ BETA.sum(axis=0))
    theta = rmvnorm(1, mum, Lm).flatten()
    
    # Sigmaの更新
    mtheta = np.tile(theta, (m, 1))
    iSigma = rwish(1, eta0 + m, np.linalg.inv(S0 + (BETA - mtheta).T @ (BETA - mtheta)))
    
    # s2の更新
    RSS = sum([np.sum((Y[j] - X[j] @ BETA[j])**2) for j in range(m)])
    s2 = 1 / gamma.rvs((nu0 + sum(N)) / 2, scale=1 / ((nu0 * s20 + RSS) / 2))
    
    # 結果の保存
    if s % 10 == 0:
        S2_b.append(s2)
        THETA_b.append(theta)
        SIGMA_PS.append(np.linalg.inv(iSigma))
        BETA_pp.append(rmvnorm(1, theta, np.linalg.inv(iSigma)).flatten())

# リストをNumPy配列に変換
S2_b = np.array(S2_b)
THETA_b = np.array(THETA_b)
SIGMA_PS = np.array(SIGMA_PS)
BETA_pp = np.array(BETA_pp)

# 図11.3のプロット
plt.figure(figsize=(14, 7))

# 左側のサブプロット
plt.subplot(1, 2, 1)
sns.kdeplot(THETA_b[:, 1], bw_adjust=2, label=r'$\theta_2$', lw=2)
sns.kdeplot(BETA_pp[:, 1], bw_adjust=2, color="gray", label=r'$\tilde{\beta}_2$', lw=2)
plt.xlabel("傾きパラメータ")
plt.ylabel("事後確率密度")
plt.legend()

# 右側のサブプロット
plt.subplot(1, 2, 2)
x_range = np.linspace(-3, 3, 100)
for j in range(BETA_pp.shape[0]):
    plt.plot(x_range, BETA_pp[j, 1] * x_range + BETA_pp[j, 0], color="gray")
plt.plot(x_range, np.mean(THETA_b[:, 1]) * x_range + np.mean(THETA_b[:, 0]), lw=2, color='blue')
plt.xlabel("SES")
plt.ylabel("数学スコア")
plt.xlim(-3, 3)

plt.tight_layout()
plt.show()

以下では$\theta_2$の95%事後信用区間と$P(β̃2 < 0)$を計算しています。
95%事後信用区間は(1.84, 2.96)、$P(β̃2 < 0)$を0.071となっており、書籍とほぼ同じ値となっています。

quantiles_theta = np.quantile(THETA_b[:, 1], [0.025, 0.5, 0.975])
mean_beta = np.mean(BETA_pp[:, 1] < 0)
print(f"θ2の95%信用区間: ({quantiles_theta[0]:.2f}, {quantiles_theta[2]:.2f})")
# θ2の95%信用区間: (1.84, 2.96)
print(f"P(β̃2 < 0) = {mean_beta:.3f}")
# P(β̃2 < 0) = 0.071

場所ごとに変化する各マウスごとの腫瘍数、二次、三次、四次多項式を平均腫瘍数の対数に当てはめた結果

図11.4は、実験用マウスの腸における腫瘍成長の研究結果を詳細に視覚化した図です。この研究では、21匹のマウスの腸をそれぞれ20区画に分け、各区画での腫瘍数を記録しています。左図では、各マウスの腸の長さに沿った腫瘍数の分布を21本の線で表現しています。X軸は腸の長さの割合、Y軸は腫瘍数を示しています。青い線で示された平均に対して、一部のマウスのデータが一貫して上回りまたは下回る傾向が見られます。これは、腫瘍数がマウス個体内で類似性が高く、個体間で差異が大きいことを示唆しており、マウス固有の効果を考慮した階層モデルの必要性を示しています。
このようなカウントデータに対して、対数リンク関数を持つポアソン分布モデルが自然な選択となります。各マウス$j$の腸の位置$x$での腫瘍数$Y_{x,j}$は、$Poisson(exp\{f_j(x)\})$とモデル化されます。ここで$f_j(x)$は滑らかに変化する関数で、多項式として表現されます。
右図では、21匹のマウスの平均腫瘍数の対数を示しており、2次、3次、4次の多項式近似も表示されています。4次多項式が最も良く平均腫瘍数の対数関数にフィットしていることが分かります。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import statsmodels.api as sm

# データの読み込み
tumor_location = pd.read_csv('./csv/tumorLocation.csv')
Y = tumor_location.values

# 値のシーケンスを作成
m = Y.shape[0]
xs = np.linspace(0, 1, Y.shape[1])

# 最初のグラフをプロット
plt.figure(figsize=(14, 7))
plt.subplot(1, 2, 1)
plt.plot([0, 1], [np.min(Y), np.max(Y)], 'w')
plt.xlabel("位置")
plt.ylabel("腫瘍の数")
for j in range(m):
    plt.plot(xs, Y[j, :], color="gray")
plt.plot(xs, np.mean(Y, axis=0), linewidth=3)

# 平均腫瘍数の対数
lya = np.log(np.mean(Y, axis=0))

# 線形モデル用の多項式特徴量
X = np.column_stack([np.ones_like(xs), np.polynomial.polynomial.polyvander(xs, 4)[:, 1:]])

# 線形モデルのフィッティング
fit2 = sm.OLS(lya, X[:, :3]).fit()
fit3 = sm.OLS(lya, X[:, :4]).fit()
fit4 = sm.OLS(lya, X[:, :5]).fit()

# モデルからの予測
yh2 = X[:, :3] @ fit2.params
yh3 = X[:, :4] @ fit3.params
yh4 = X[:, :5] @ fit4.params

# 2番目のグラフをプロット
plt.subplot(1, 2, 2)
plt.plot(xs, lya, 'k', linewidth=3, label="対数平均腫瘍数")
plt.plot(xs, yh2, 'gray', label="モデル2")
plt.plot(xs, yh3, 'gray', linestyle='--', label="モデル3")
plt.plot(xs, yh4, 'gray', linestyle=':', label="モデル4")
plt.xlabel("位置")
plt.ylabel("対数平均腫瘍数")
plt.legend()

plt.show()

$exp(\theta^{T}x)$,$exp(\theta^{T}x)$および$\{Y|x\}$の2.5%、50%、97.5%分位点

左図では、$exp(θ^{T}x)$の事後分布の2.5%、50%、97.5%分位点を表示しています。これは、固定されているが未知の値θに関する不確実性を表しています。
中央の図は、$exp(β^{T}x)$の事後予測分布の同じ分位点を示しています。左図と比較して信頼区間が広くなっていますが、これはマウス間の異質性（$\Sigma$）の推定値を反映しています。もしマウス間の異質性がなければ、$\Sigma$はゼロとなり、各$\beta_j$は$\theta$に等しくなるため、両パネルは同一になるはずです。右図では、20の異なる$x$値それぞれに対する$\{Y|x\}$の事後予測分布の2.5%、50%、97.5%分位点を示しています。中央の図との違いは、ポアソン分布に従う変数$Y$の期待値$exp(β^{T}x)$周りの変動によるものです。これら3つのプロットにおける信頼区間の拡大は、累積的な不確実性の源を描写しています。左図では$\theta$の不確実性、中央の図ではそれにマウス間の異質性による不確実性を加えたもの、右図では更に個々のマウスの観測された腫瘍数の期待腫瘍数関数周りの変動を含んでいます。

import numpy as np
from scipy.stats import multivariate_normal, wishart, poisson
from numpy.linalg import inv, det
import matplotlib.pyplot as plt
import japanize_matplotlib
import statsmodels.api as sm

def ldmvnorm(X, mu, Sigma, iSigma=None, dSigma=None):
    if iSigma is None:
        iSigma = np.linalg.inv(Sigma)
    if dSigma is None:
        dSigma = np.linalg.det(Sigma)

    Y = X - mu
    log_density = -0.5 * np.sum(np.dot(Y, iSigma) * Y, axis=1)
    log_density -= 0.5 * (np.prod(X.shape) * np.log(2 * np.pi) + X.shape[0] * np.log(dSigma))

    return np.sum(log_density)

BETA = []

# Yの各行に対してBETAを計算
for j in range(m):
    # 対数変換したYをXに対して線形回帰
    X_with_intercept = sm.add_constant(X)
    # 切片を含むXに対して対数変換したYの線形回帰
    model = sm.OLS(np.log(Y[j, :] + 1/20), X_with_intercept).fit()
    BETA.append(model.params)

# BETAをnumpy配列に変換
BETA = np.array(BETA)

# 事前分布を計算
mu0 = np.mean(BETA, axis=0)
S0 = np.cov(BETA.T)
eta0 = p + 2
iL0 = iSigma = np.linalg.inv(S0)

np.random.seed(100)

# THETA.postとSIGMA.postを初期化
THETA_post = []
SIGMA_post = []

for s in range(1, 50001):
    # thetaを更新
    Lm = inv(iL0 + m * iSigma)
    mum = np.dot(Lm, np.dot(iL0, mu0) + iSigma @ np.sum(BETA, axis=0))
    theta = multivariate_normal.rvs(mean=mum, cov=Lm, size=1)

    # Sigmaを更新
    mtheta = np.tile(theta, (m, 1))
    iSigma = wishart.rvs(df=eta0 + m, scale=inv(S0 + np.dot((BETA - mtheta).T, (BETA - mtheta))), size=1)

    # betaを更新
    Sigma = inv(iSigma)
    dSigma = det(Sigma)
    for j in range(m):
        beta_p = multivariate_normal.rvs(mean=BETA[j, :], cov=0.5 * Sigma, size=1)
        lr = np.sum(poisson.logpmf(Y[j, :], np.exp(np.dot(X, beta_p)))) - \
             np.sum(poisson.logpmf(Y[j, :], np.exp(np.dot(X, BETA[j, ])))) + \
             ldmvnorm(beta_p[None, :], theta, Sigma, iSigma, dSigma) - \
             ldmvnorm(BETA[j, :][None, :], theta, Sigma, iSigma, dSigma)

        if np.log(np.random.uniform()) < lr:
            BETA[j, :] = beta_p

    # 一部の出力を保存
    if s % 10 == 0:
        THETA_post.append(theta)
        SIGMA_post.append(Sigma.flatten())

# リストを配列に変換
THETA_post = np.array(THETA_post)
SIGMA_post = np.array(SIGMA_post)

eXB_post = []

# eXB.postを生成
for s in range(THETA_post.shape[0]):
    # SIGMA_post[s, :]を5x5行列に再形成
    sigma_matrix = SIGMA_post[s, :].reshape(5, 5)

    beta = multivariate_normal.rvs(mean=THETA_post[s, :], cov=sigma_matrix)
    eXB_post.append(np.exp(np.dot(X, beta)))

eXB_post = np.array(eXB_post)

# eXB.postの分位数
qEB = np.quantile(eXB_post, [0.025, 0.5, 0.975], axis=0)

# eXT.postを生成
eXT_post = np.exp(np.dot(X, THETA_post.T))

# eXT.postの分位数
qET = np.quantile(eXT_post, [0.025, 0.5, 0.975], axis=1)

# yXT.ppを生成
yXT_pp = np.random.poisson(lam=eXB_post).reshape(eXB_post.shape)

# yXT.ppの分位数
qYP = np.quantile(yXT_pp, [0.025, 0.5, 0.975], axis=0)

# プロットの準備
plt.figure(figsize=(15, 5))

titles = ['期待腫瘍数', '期待ベータ', '予測事後分布']
quantiles = [qET, qEB, qYP]
y_min = 0   # y軸の最小値
y_max = 20  # y軸の最大値

for i in range(3):
    plt.subplot(1, 3, i+1)
    plt.plot(np.linspace(0, 1, quantiles[i][0].shape[0]), quantiles[i][0], 'k-', label='2.5%')
    plt.plot(np.linspace(0, 1, quantiles[i][0].shape[0]), quantiles[i][1], 'k--', label='50%')
    plt.plot(np.linspace(0, 1, quantiles[i][0].shape[0]), quantiles[i][2], 'k-', label='97.5%')
    plt.ylim(y_min, y_max)
    plt.title(titles[i])
    plt.xlabel('位置')
    if i == 0:
        plt.ylabel('腫瘍数')
    plt.legend()

plt.tight_layout()
plt.show()

最後に

本ブログでは、標準ベイズ統計学の第11章で扱われる線形・一般化線形混合効果モデルについて、Pythonを用いた実装と可視化を行いました。次は、「順序データに対する潜在変数法」の実装を行っていきたいと思います。