🌟

Consistency Models: 1~4stepsで画像が生成できる、新しいスコアベース生成モデル

2023/04/14に公開

Diffusion model

拡散モデル

tech

はじめに

こんにちは。

今回は、Yang Songさんをはじめとする拡散モデルの第一人者が新たに提唱する生成モデルである、Consistency Model（一貫性モデル） を説明します。

https://arxiv.org/abs/2303.01469

まだ実用レベルのpre-trained modelがリリースされているわけではなく、PoCの段階ですが、その成り立ちやデザインからして、のちに拡散モデルの正統進化版の1つとして広く受け入れられるものになる気がしています。

前置き

Consistency Modelは拡散モデルと強すぎる結びつきがあり、拡散モデルをスコアベース生成モデル（Score-based Generative Model）として捉えることが議論の端緒となっていることから、話に追いつくまでには数多くの文脈があります。

特に、以下の2論文はConsistency Modelと非常に深い関わりがあるため、もしめっちゃ詳しく理解したいなら一読をおすすめします。

1. Score-Based Generative Modeling through Stochastic Differential Equations

https://arxiv.org/abs/2011.13456

2. Elucidating the Design Space of Diffusion-Based Generative Models

https://arxiv.org/abs/2206.00364

なお、なんとなく読んでも多分大丈夫だと思います。

TL;DR

あらゆる時刻からの原点へのマッピングを学習することによって、スコアベース生成モデルで1stepもしくは数stepでの画像生成が可能になった。性能は当然既存の重い拡散モデルに劣るが、高速化は著しい
Consistency Modelの学習手法には既存の拡散モデルからの蒸留（Consistency Distillation）とゼロからの学習（Consistency Training）の2つがある
推論ステップ数と品質はトレードオフの関係にあり、推論時にどちらを優先するか選択することができる
L2距離以外にも、L1距離やLPIPSのような様々な差異の評価関数を使用して学習を試みている

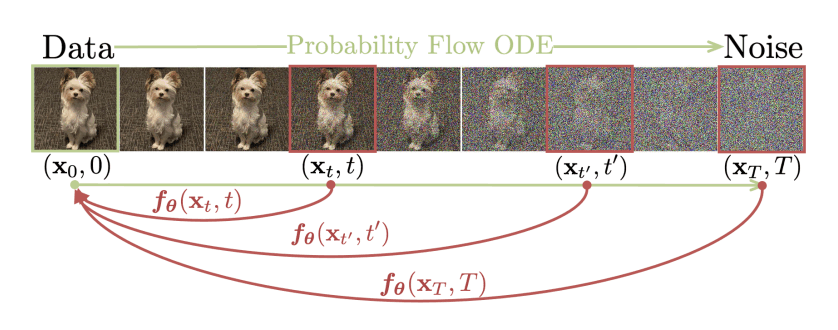
定義（難しく、つらい）

まず、拡散モデルの拡散過程のタイムステップを無限大に増やした場合、逆拡散過程は確率微分方程式（Stochastic Differential Equation）の解で表現することができ、それはProbability Flow ODEと呼ばれる常微分方程式の解としても表現することができる、ということが分かっています（Song et al., 2021）。

そして、ある時刻 $t$ におけるProbability Flow ODE（以下PF ODE）の解軌道は以下のようになります。

d\bold{x}_{t} = \lbrack \bold{\mu}(\bold{x}_{t},t) + \frac{1}{2}\sigma(t)^2 \nabla\log p_{t}(\bold{x}_{t}) \rbrack dt

ここでそれぞれ、

$t$ : $t\in [0, T], T > 0$ を満たす定数
$\bold{x}_{t}$ : 時刻 $t$ におけるデータの状態
$d\bold{x}_{t}$ : 時刻 $t$ におけるデータの状態の変化量
$\bold{\mu}(\bold{x}_{t},t)$ : 時刻tでのデータの状態 $\bold{x}_{t}$ に依存する確率過程の平均変化率を表す。実際には簡単のために $\bold{\mu}(\cdot,\cdot)=0$ として扱われる
$\sigma(t)$ : 時刻tにおけるノイズの強度を表す関数で、実際には簡単のために $\sigma(t)=\sqrt{2t}$ として扱われる
$\nabla\log p_{t}(\bold{x}_{t})$ : 時刻 $t$ におけるデータの状態 $\bold{x}_{t}$ の対数尤度関数 $\log p_{t}(\bold{x}_{t})$ の勾配（→スコア）
$dt$ : 時刻の変化量

を意味します。

この式によって $\{\bold{x}_{t}\}_{t\in [\epsilon, T]}$ の解軌道（solution trajectory）が与えられたとき、Consistency Functionとして $\bm{f}: (\bold{x}_{t}, t) \mapsto \bold{x_{\epsilon}}$ を定義します。Consistency Functionはself-consistencyを持ち、出力 $\bold{x_{\epsilon}}$ が同じPF ODEの軌道に属する任意の $(\bold{x}_{t},t)$ のペアに対して一貫しているという性質があります。

そして、Consistency Modelである $\bm{f_{\theta}}$ は、Consistency Functionの特性であるself-consistencyを得るように学習され、振る舞いを推定するようデザインされたモデルです。

Consistency Modelは深層学習モデルである $F_{\theta}(\bold{x}, t)$ を用いたとき、以下のように表すことができます（ $F_{\theta}(\bold{x}, t)$ の出力次元は $\bold{x}$ と同じ）。

\bm{f_{\theta}}(\bold{x}, t) = \begin{cases} \bold{x}, & t=\epsilon \\ F_{\theta}(\bold{x}, t), & t\in (\epsilon, T] \end{cases}

また、以前の研究と類似した書き方として、以下も挙げられています。

\bm{f_{\theta}}(\bold{x}, t) = c_{skip}(t)\bold{x}+c_{out}(t)F_{\theta}(\bold{x}, t)

ここで、 $c_{skip}(t), c_{out}(t)$ は微分可能な関数で、 $c_{skip}(\epsilon) = 1, c_{out}(\epsilon) = 0$ となります。

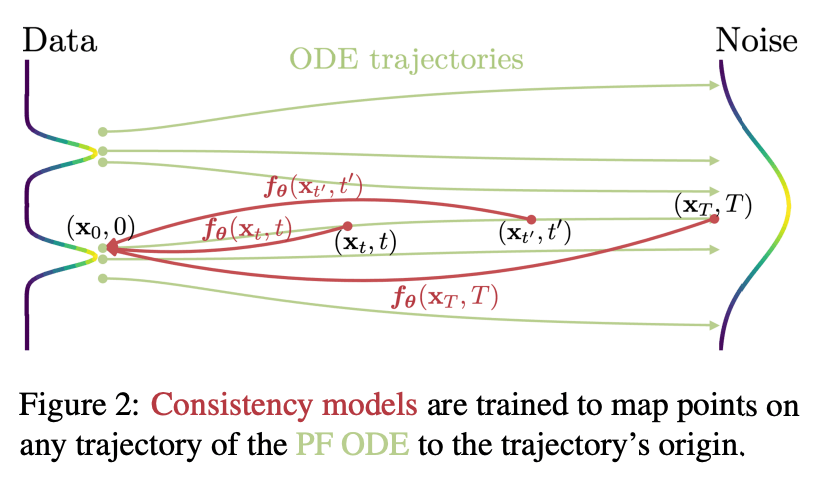
定義（ざっくり）

結論から言うと、Consistency Modelは、色々と複雑な数学的プロセスを使って、データの状態を任意の時刻 $t$ から初期状態に戻す方法を学習するモデルです。

まず、Consistency Functionという、現実には存在しない理想的な関数を定義します。
この関数は、どの時刻 $t$ の状態 $\bold{x}_{t}$ でも同じ初期状態 $\bold{x_{\epsilon}}$ に戻すことができるという性質を持っていると仮定します。これをself-consistencyと呼びます。概念的には、過去方向未来方向問わず、ある人間の年齢を自由に操作できる魔法の装置のような存在です。

Consistency Modelは、このConsistency Functionの性質（self-consistency）を持つように学習され、模倣するように振る舞います。仮に画像を扱うとすれば、扱う画像が完全なノイズでも、少しだけノイズが乗っているとしても、必ず同じ初期状態（ノイズが全く乗っていない状態）に戻す方法を推定するモデルとなります。つまり、うまく学習されたConsistency Modelは、1step、もしくは数stepsだけで、何十stepsも経て生成された高品質な画像と同クオリティの画像が生成できることが期待できます。

学習方法

学習方法には、既存の拡散モデルから知識を蒸留するConsistency Distillation（CD）　と、ゼロからConsistency Modelとして学習するConsistency Training（CT） との2つがあります。
単なる知識蒸留による高速化に留まらず、新しい学習プロセスをもって既存の拡散モデルに依存しないこともできることから、Consistency Modelを新たな生成モデルとして数えることができる、と論文の筆者は主張しています。

なお、実装は論文の筆者が所属するOpenAIから公開されています。研究用のため、Stable Diffusionのように高品質ではなく、まだテキスト条件付けもできませんが、上に挙げた2つの方法両方で学習された複数のpre-trained modelがアップロードされていて、自分で学習を行うためのコードもリポジトリに含まれています。

1. Consistency Distillation（CD）

まずは既存の拡散モデル（事前学習済みスコアモデル）から知識を蒸留する場合です。

十分に生成ステップ数を増やし、時刻 $t$ と $t+1$ を近づけたとき、ODE Solver（EulerとかDPM++とかのアレです）が逆拡散過程における $\bold{x}_{t+1}$ から $\bold{x}_{t}$ への変化量を正確に推定することができます。
そのとき、ODE Solverが推測した時刻 $t$ の状態を $\bold{\hat{x}}^{\phi}_{t}$ と表記すると、 $(\bold{\hat{x}}^{\phi}_{t}, \bold{x}_{t+1})$ は同じPF ODE軌道上の隣接したデータ点と考えることができます。

そして、Consistency Modelはどの時刻 $t$ の状態 $\bold{x}_{t}$ でも同じ初期状態 $\bold{x_{\epsilon}}$ に戻ることができるという性質を持っているようにしたいことから、どちらのデータ点をConsistency Modelに入力しても同じ出力が出てくるように学習させます。 つまり、 $\bold{\hat{x}}^{\phi}_{t}$ と $\bold{x}_{t+1}$ それぞれをモデルに入力したときの出力の差異を最小化するように学習します。

損失関数であるconsistency distillation lossの定式化は以下です。

\mathcal{L}^{N}_{CD}(\bm{\theta}, \bm{\theta}^{-};\bm{\phi}) = \mathbb{E} [\lambda(t_{n})d(\bm{f_{\theta}}(\bold{x}_{t_{n+1}}, t_{n+1}),\bm{f_{\theta^{-}}}(\bold{\hat{x}^{\phi}}_{t_{n}}, t_{n}))]

ここで、

$\lambda(t_{n})$ : 重みづけのための係数、 $\lambda(t_{n}) \equiv 1$ がどのデータセット・タスクにおいても良かったとのこと
$\bm{\theta}$ : Consistency Modelのパラメーター
$\bm{\theta}^{-}$ : Consistency Modelのパラメーターの学習過程での移動平均
$\bm{\phi}$ : ODE Solverのパラメーター（？）
$\bm{f_{\theta}}(\bold{x}_{t_{n+1}}, t_{n+1})$ : 時刻 $t+1$ における $\bold{x}$ の状態をConsistency Modelに入力した場合の出力（定式化のために $t$ は $t=0$ から $t=1$ までの連続的な値をとる時刻と考える必要があり、表記が $t_{n+1}$ となっているが、簡単な理解のためには $t+1$ と置き換えて読んでもよい）
$\bm{f_{\theta^{-}}}(\bold{\hat{x}}^{\phi}_{t_{n}}, t_{n})$ : 時刻 $t$ における $\bold{x}$ の状態をODE Solverによって推定した結果 $\bold{\hat{x}}^{\phi}_{t}$ をConsistency Model（パラメーターは移動平均を使用）に入力した場合の出力
$d(\cdot, \cdot)$ : L2距離・L1距離・LPIPSのどれか、今までのセオリー通りならL2距離だが、色々試してみているのがこの論文のおもしろポイントの一つ

アルゴリズムは以下です。

なお、理論的には学習が収束すると $\bm{\theta} = \bm{\theta}^{-}$ となります。

深層強化学習の文脈では $\bm{f_{\theta}^{-}}$ を"target network"、 $\bm{f_{\theta}}$ を"online network"と呼ぶらしく、 $\bm{\theta}^{-}$ をアルゴリズムのようにEMAでアップデートしていくことが学習を"かなり"安定させ、Consistency Modelの最終的なパフォーマンスを向上させたそうです。
あんまりピンとこないので、実際のところこれにどんな利点があるのかGPT-4に説明してもらいました。彼が嘘をついているようだったら教えてください。

深層強化学習（Deep Reinforcement Learning, DRL）において、ターゲットネットワーク（ $f_{\theta}^{-}$ ）とオンラインネットワーク（ $f_{\theta}$ ）の利用は、主に学習の安定性を向上させる目的で行われます。具体的には以下のような利点があります。

TD誤差の低減: DRLでは、Q値（行動価値関数）を推定するためにTemporal Difference (TD) 学習を使用します。オンラインネットワークを更新する際に、ターゲットネットワークから得られたQ値を使ってTD誤差を計算することで、誤差の推定がより安定します。これはターゲットネットワークが一定期間固定されているため、学習過程で推定値が急激に変化することが少なくなります。

相関の低減: ターゲットネットワークの利用は、学習データ間の相関を低減する効果があります。これは、オンラインネットワークとターゲットネットワークが別のパラメータを持っているため、連続した状態・行動ペア間でQ値の更新が伝播しにくくなることが原因です。これにより、学習がより安定し、収束しやすくなります。

過学習の抑制: ターゲットネットワークは、EMA（指数移動平均）を用いてゆっくりと更新されます。これにより、オンラインネットワークのノイズに対する感度が低下し、過学習が抑制される可能性があります。

収束速度の向上: ターゲットネットワークとオンラインネットワークの二つのネットワークを使用することで、学習の収束速度が向上することが報告されています。これは、ターゲットネットワークが学習の進捗に応じて更新されるため、オンラインネットワークの更新に適切な教師信号が提供されることが原因です。
これらの利点により、深層強化学習においてターゲットネットワークとオンラインネットワークの使用は、一般的で効果的な方法となっています。

2. Consistency Training（CT）

Consistency Distillationでは、真のスコア関数 $\nabla\log p_{t}(\bold{x}_{t})$ を近似する事前学習済みスコアモデルを利用することでself-consistencyを獲得することが可能でした。
しかし、既存の拡散モデルに依存する形では新しい生成モデルとは言えず、別の方法でゼロからスコア関数の振る舞いを推定する手法が必要になってきます。

そこで、以下が $\nabla\log p_{t}(\bold{x}_{t})$ の不偏推定量（推定する対象パラメータの期待値に等しい推定量のこと）であることを利用し、モンテカルロ法を用いて推定します。

\nabla\log p_{t}(\bold{x}_{t}) = - \mathbb{E} \left[ \frac{\bold{x}_t - \bold{x}}{t^{2}} | \bold{x}_t \right]

ここで、 $\bold{x} \sim p_{data}, \bold{x}_t \sim \mathcal{N}(\bold{x}, t^{2}\bold{I})$ です。
つまり、 $p_{data}$ から持ってきたデータ $\bold{x}$ の時刻を $t$ だけ進め（=ノイズを乗せ）て $\bold{x_{t}}$ とし、 $-(\bold{x}_t - \bold{x})/t^{2}$ を計算する、というのをたくさんやり、その結果の期待値を計算することで、 $\nabla\log p_{t}(\bold{x}_{t})$ の振る舞いを推定できるということです。

その後、つらく厳しい計算過程を経て、

Consistency Trainingの損失関数は以下のように定式化されます。結果的にConsistency Distillationとあまり変わらない感じになりました。

\mathcal{L}^{N}_{CT}(\bm{\theta}, \bm{\theta}^{-}) = \mathbb{E} [\lambda(t_{n})d(\bm{f_{\theta}}(\bold{x} + t_{n+1} \bold{z}, t_{n+1}),\bm{f_{\theta^{-}}}(\bold{x} + t_{n} \bold{z}, t_{n}))]

ここで、 $\bold{z}$ は $\bold{z}\coloneqq \frac{\bold{x}_{t_{n+1}}-\bold{x}}{t_{n+1}}$ と定義される、 $\mathcal{N}(\bold{0},\bold{I})$ に従う変数です。要するに、ただのノイズです。

アルゴリズムは以下です。ここでも $\bm{\theta^{-}}$ をEMAで更新する手法が使われています。

性能

さて、一番気になるのは性能です。
まず、Consistency Modelを拡散モデルの蒸留手法と見たとき、既存の蒸留手法であるProgressive Distillationとの差を見てみます。

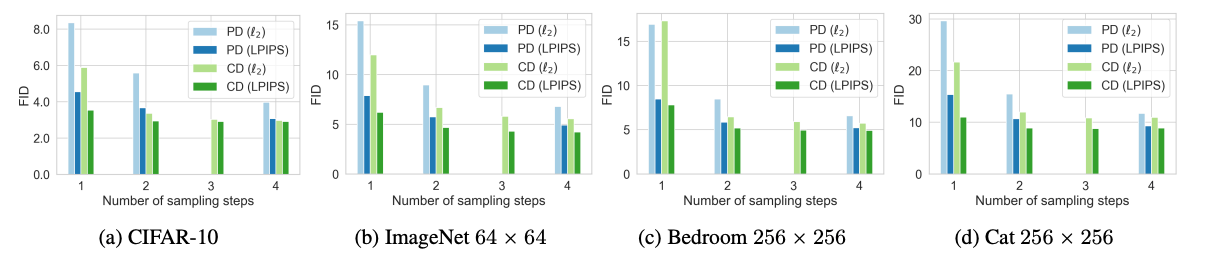
CDがConsistency Distillation、PDがProgressive Distillation

結構いい感じですね。1step・数steps両方で凌駕しているように見えます。
あと意外なのが、L2距離よりLPIPSで学習したほうが大体強いようです。

次に、EDM(Karras et al., 2022)との差異を見てみましょう。こちらは蒸留モデルではなく、普通に強くて比較的高速な拡散モデルです。

上からEDM、CT+1step、CT+2steps

まあさすがにEDMの方が強いですが、EDMは1枚の画像を生成する際に79回UNetを使用しているのに対して、下2段のConsistency Modelはそれぞれ1回と2回です。考えるとめっちゃすごい。
自分でも実際に触ってみましたが、1, 2stepsは生成がびっくりするぐらい早いです。

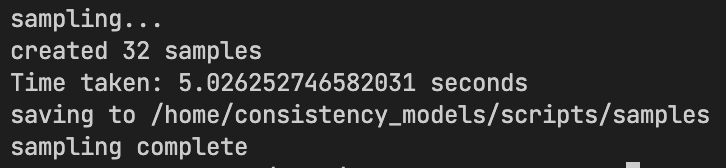
256x256の画像を2stepsで32枚生成するのに5.02秒しかかかりません。1stepだと3.25秒です。びっくり

また、Consistency Modelのオススメの使い方として、Zero-shot Image Editingがあるそうです。ゼロからのHigh-fidelityな画像生成は重たい既存の拡散モデルに任せておいて、すでに生成対象がある程度見えている状態からの画像編集タスクのほうがConsistency Modelはより威力を発揮するのかもしれません。

Zero-shot Image Editing. 上から、モノクロ画像の色付け、超解像、手描き画像からの生成を行っている

Zero-shot Image Editing.(2) マスク部分をinpaintするタスクにも結構強い

おわりに

1〜数stepsにしてはかなりの性能があるというのと、何より論文の著者が界隈の超有名人で実装がOpenAIからリリースされた、というところでかなり注目を集めたConsistency Modelですが、画像生成のようなクソデカモデルの世界になると、「それが強い技術かどうか」よりも「ユーザーが使いやすいドメインのpre-trained modelが公開されているかどうか」　が世間に普及する鍵になっているので、まだまだこの技術がどんどん受け入れられていくかどうかは未知数です。

しかし、やはり単純な性能の高さや、拡散モデルを蒸留する形で作成できること、GANと比較すると学習が難しくないことなどから、今までの生成高速化技術とは一線を画すものであるような気がします。

テキスト条件付けがある場合に既存の拡散モデルに比べてどの程度Text Alignmentのパフォーマンスが変わるのか？など、未検証の部分はまだたくさんあるので、今後に期待です。