AtCoder Beginner Contest 317参加記(A~C)
ゲームフリーク Programming Contest 2023(AtCoder Beginner Contest 317)に参加したので記録を残します。
今回は3完です。
豪華な特典が話題になりました。ポストカード、何が当たっても嬉しいので当たらないかなあ…
A - Potions
なのですが、なんか無駄に複雑なコードになってしまいました。
fun main() {
val (n, h, x) = readln().split(" ").map { it.toInt() }
val p = readln().split(" ").map { it.toInt() }
println(p.mapIndexed { index, i -> index to h + i }.filter { it.second >= x }.minBy { it.second }.first + 1)
}
最初は
実際にはこうすればよかった。
fun main() {
val (n, h, x) = readln().split(" ").map { it.toInt() }
val p = readln().split(" ").map { it.toInt() }
println(p.indexOfFirst { it + h >= x } + 1)
}
B - MissingNo.
fun main() {
val n = readln().toInt()
val a = readln().split(" ").map { it.toInt() }
.sorted()
var num = a.first()
for(i in 1 until n) {
if(a[i] != num + 1) {
println(a[i] - 1)
return
} else {
num = a[i]
}
}
println(a.first() - 1)
}
最後の一行はいらないですね…
飛んでいる番号が見つからなかった場合は最小値の1つ前という意味で書いています。
しかし飛んでいる番号がなかったとしたら、普通に考えれば最小値の一つ前か最大値の一つ後かの2通りが考えられますが、ということは なくした整数が一意に定まるような入力のみが与えられます。 という制約に反するのでそのような入力が与えられることはないですね。
なので、そもそも不要な上に考慮しきれてもいないという残念な感じです。
C - Remembering the Days
制約が小さいので、DFSで全部試して最大値を探せばいいということになりますが、グラフを処理するコードを書くのが久しぶりで感覚を忘れていたのと、実装のミスでハマって時間を溶かしました。
基本的には街が頂点で道路が辺の無向グラフとして捉えて、あり得るルートを全部試すという実装になりました。
一応、Threadを生成してスタックを拡張しています。Kotlinだとこれをやらないとスタックオーバーフローになりがちです。今回は制約が小さいので大丈夫かなと思ったものの、念のため。
(これはスニペット化したので入力の手間もないし)
道路は距離を持つので、Pairを使って重み付きグラフとしています。
import java.util.ArrayDeque
import kotlin.math.max
fun main() {
Thread(
null,
{
val (n, m) = readln().split(" ").map { it.toInt() }
val graph = Array(n + 1) { mutableListOf<Pair<Int, Int>>() }
repeat(m) {
val (a, b, c) = readln().split(" ").map { it.toInt() }
graph[a].add(b to c)
graph[b].add(a to c)
}
for(i in 1..n) {
dfs(i, BooleanArray(n + 1), graph, 0L)
}
println(ans)
},
"",
128 * 1024 * 1024
).start()
}
var ans = 0L
fun dfs(v: Int, seen: BooleanArray, graph: Array<MutableList<Pair<Int, Int>>>, distSum: Long): Long {
seen[v] = true
for(node in graph[v]) {
val (next, dist) = node
if(seen[next]) {
continue
}
val ret = dfs(next, seen, graph, distSum + dist)
ans = max(ans, ret)
}
seen[v] = false
return distSum
}
ポイントは seen[v] = false の部分です。seenは訪問済の街に再度訪問することがないようにするための値です。これを設定しないと同じ街に再度訪問してしまい、それから同じルートをぐるぐると回り続けて探索が終わりません。かといって、設定しっぱなしだと必要な探索もブロックされて途中で処理が終わってしまいます。
今回の場合は、seen[v] = falseを適宜実行しないと探索が途中で終わってしまうのが問題となりました。
ちょっと出力例3の画像を元に考えてみます。
(ちなみにこれって初代ポケモンのカントー地方らしいですね。言われてみればたしかになんですが、初代ポケモンは何周もしたのに気づかず不覚です…)
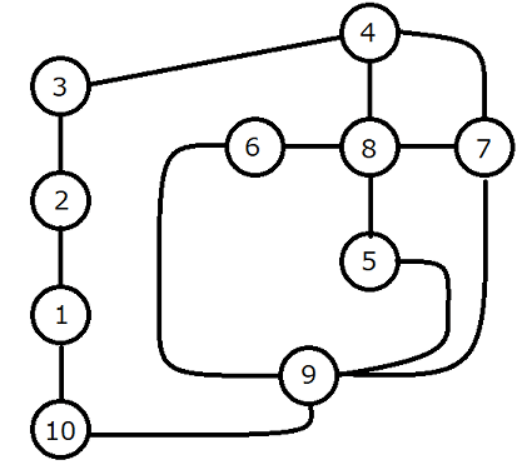
わかりやすいように、頂点番号が小さいほうを優先して探索することとします。(実際にはそうとは限らないのですが)
マサラタウンもとい街1から探索を開始するとして、上記のルールで行けるところまで行ったら以下のようになります。
赤が通った道路で、訪問済は水色にしています。手描きでごめんね。
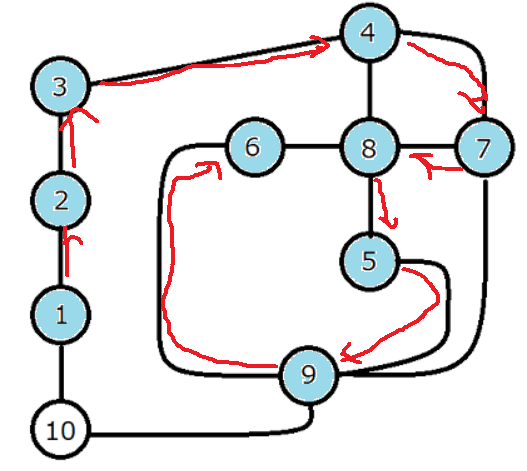
街10以外の全ての街を訪問して、街6にたどり着きます。6から8に伸びる道路がありますが、8は訪問済なのでそこから先には行きません。
街6から行ける場所は他にはないので再帰を抜けて、街9からの探索に戻ります。街9から行ける未訪問の街として街10があるので、そこに訪問します。 (ふたごじまがないね)
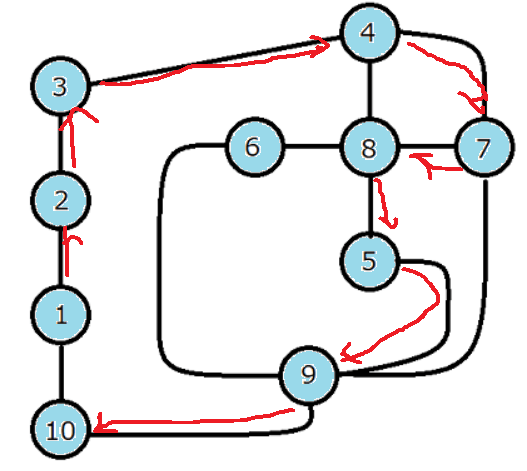
街10から街1への「道路」[1]がありますが、街1は訪問済(出発地)なので訪問しません。
この時点で全ての街が訪問済になるので、これ以降は探索されずにそのまま処理が終了します。
しかし、これだと明らかに一部しか探索できていません。
以下の「道路」を通るルートが試されていません。
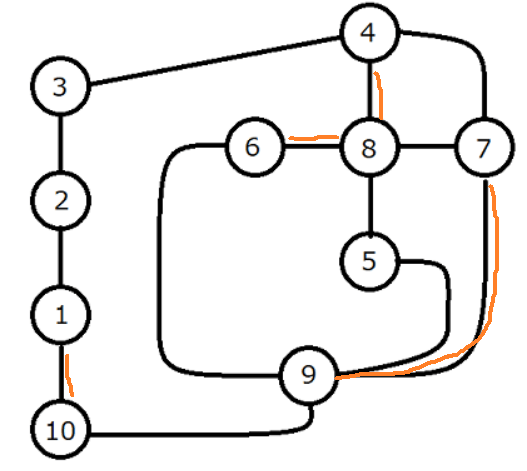
なんでそうなってしまうかというと、街の訪問済フラグを適宜解除していないためです。
たとえば4と8をつなぐ道路を通るパターンも試したいと思ったときに (賄賂が必要)
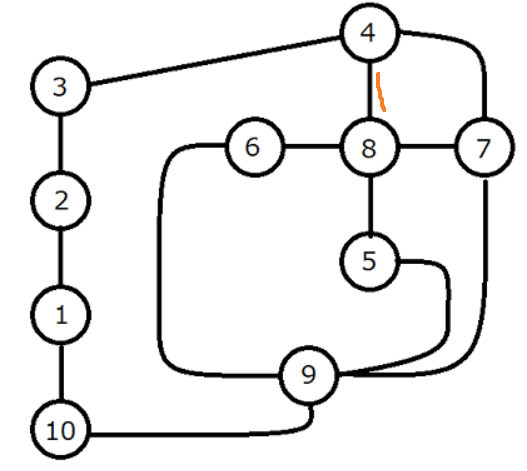
4まで来たときはこうなっていて
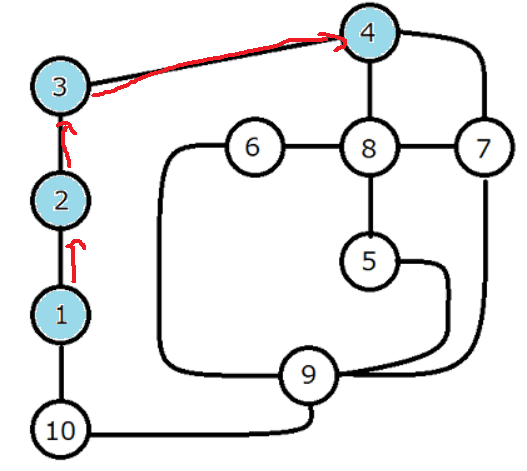
まずは7へ行くわけですが
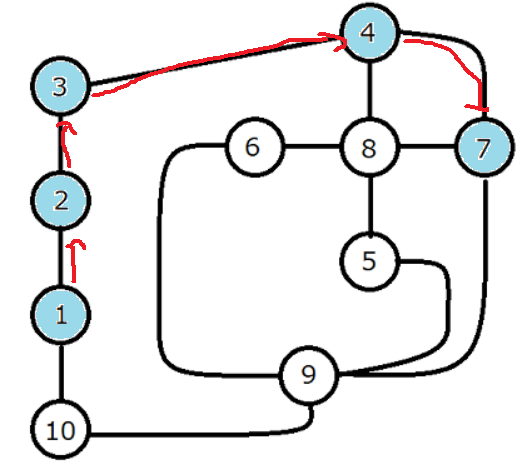
一通り探索が終わって再帰を抜けて抜けて4まで戻ってきたときにこうなっていれば、続いて8への探索を開始できるのですが
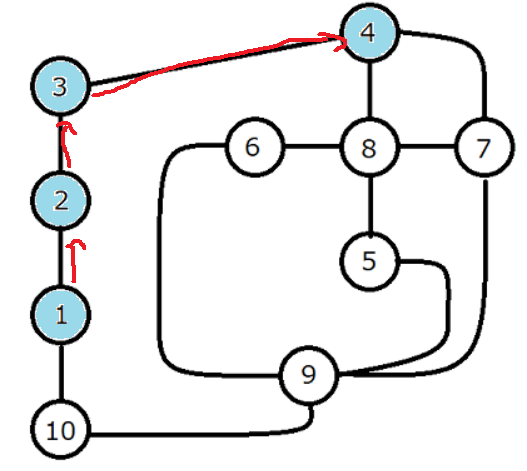
実際にはこうなっちゃっているわけです
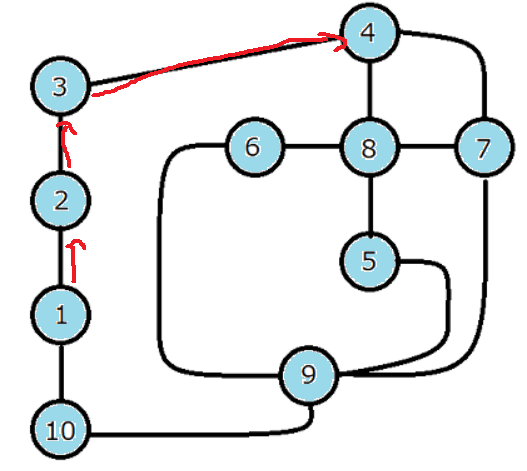
それをどうやって回避するか。まあそのために必要なのが seen[v] = false なのですが、なぜそれでいいのか。
このコードは関数の最後、つまり再帰を抜けるときに実行されます。
最初のこの状態からだと
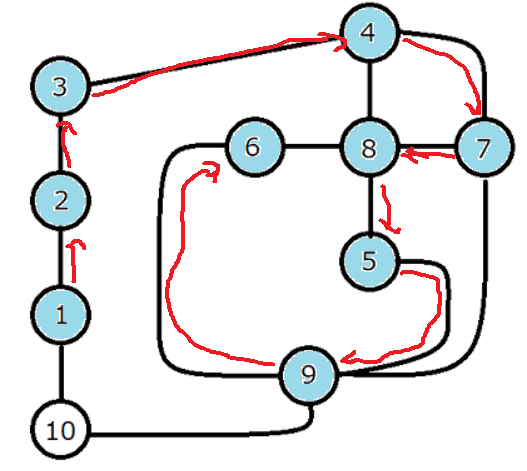
6を抜けるときにそれ自身の訪問済フラグを解除するのでこうなります
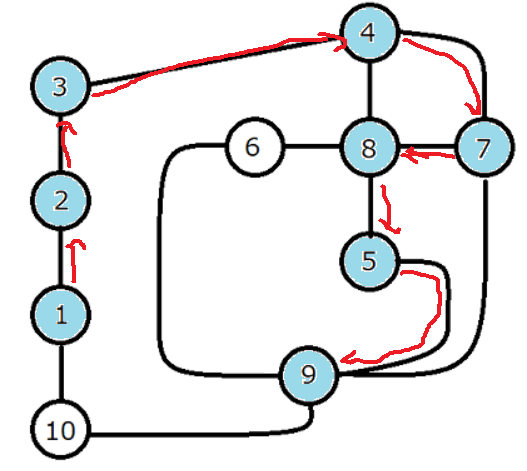
9から10へ行きますが
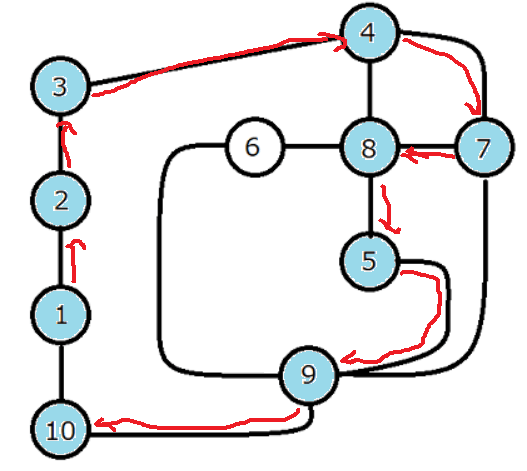
10から行ける場所はないので抜けて9に戻り、また同じ状態になります
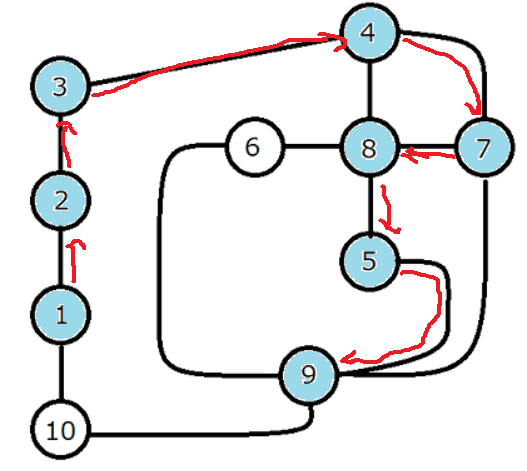
同じといっても9から6、10への遷移はすでに実行済なので再度実行はしません。
9から行ける場所は他にないので9を抜け、5に戻ります。
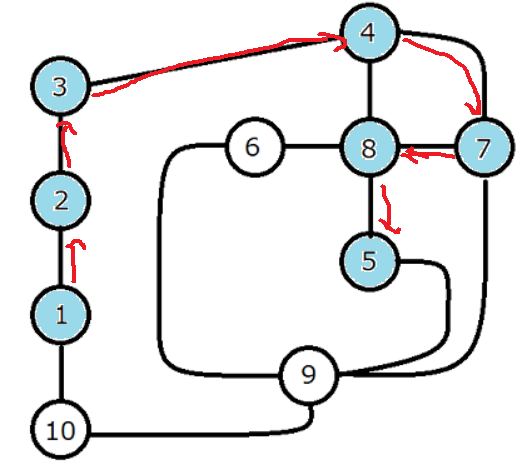
こんな感じで、探索が終わって抜けるときに自身の訪問済フラグが解除されていくので、このまま5を抜けて、8を抜けて、7を抜けて、となっていくと望んでいたこの状態になるわけです。
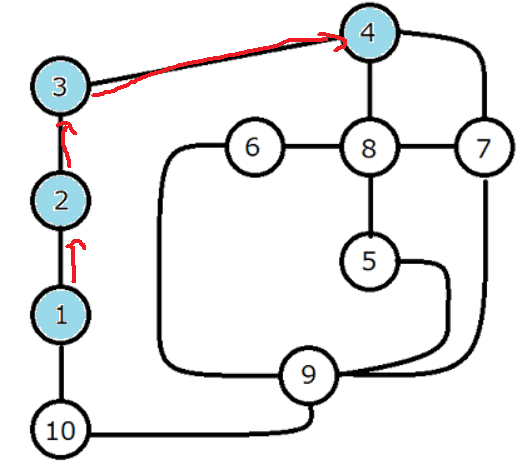
まあ実際にはその前に8から6への探索が発生したり、7から9への探索が発生したりするのですが、それはそれで本来必要なのに実行されなかった探索が実行されるということなので、これで一通りうまくいきそうというのがわかります。
偉そうに書きましたが、これを理解するまでに1時間くらいかかりました。グラフ処理はこの探索済フラグをどのように更新するのかが肝というのが再認識させられました。
D - President
制約が小さければ、どの勝たせる選挙区のパターンをbit全探索とかで全部見れば解けるのですが、
それ系はだいたいDPだと思っているので、まあDPで解けるんだろうなあとは思ったのですが、C問題で時間を溶かしたので全然時間が足りず解けませんでした。
感想
最近は習慣的にRated参加することもできていなかったので、当分は多少冷えてもいいのでとにかくRated参加することだけを目標にしようと思っています。
それを考えると、今回は若干とはいえレートも増加したので悪くない感じだったなと思います。
C問題で一旦詰まったわけですが、まあ今の自分ならそうなるよなと変に達観していて落ち着いて考えることができて結果解けたみたいなところがあります。以前の自分だと、これは解けなきゃいけない問題だろと焦って結果解けないみたいになっていたかもしれません。
グラフ系の問題だと、類題が多いので過去書いたコードをコピペして少し変えるだけで通るみたいなことがあったりするんですよね。なので直近だとあまりちゃんと考察せずに実装先行でうまくいかず爆死みたいなこともあったのですが、今回は落ち着いて考えて解法を見つけられたのでよかったなと。当たり前なんですけど、レートが冷えるのが怖くて焦ってそういうムーブをかましがちだったかもなあと反省しましたね…
レートも重要なんですけど、焦らずに問題をちゃんと考えて解くことの楽しさを忘れないようにしたいなあと思ったところです。
(執筆時間: 1時間31分12秒)
-
なみのりが必要。道路…?? ↩︎
Discussion