🎉

AtCoder Beginner Contest 340参加記（A～D）

2024/02/11に公開

AtCoder

競プロ

tech

鹿島建設プログラミングコンテスト2024（AtCoder Beginner Contest 340）に参加したので記録を残します。
https://atcoder.jp/contests/abc340

今回は4完です。過去最高パフォ（993）が出ました。1000台には載りませんでしたが。

A - Arithmetic Progression

$A$ から始めて、 $B$ を超えるまで $D$ を足し続けるだけ、なんですが無駄にstepとか使ってやろうとしてうまくいかず手間取りました。なぜ…

fun main() {
    val (a, b, d) = readln().split(" ").map { it.toInt() }

    val list = mutableListOf<Int>()
    list.add(a)

    var num = a
    while (true) {
        num += d
        if(num > b) {
            break
        }
        list.add(num)
    }

    println(list.joinToString(" "))
}

B - Append

やるだけなんですが、 $k$ が末尾からのカウントなのが若干面倒。そこで $A$ を反転させて先頭から見た位置に補正しました。計算量としてはアレですが、気にする必要があるほどの制約じゃないのでセーフ。

fun main() {
    val q = readln().toInt()


    val a = mutableListOf<Int>()

    for(i in 0 until q) {
        val (t, x) = readln().split(" ").map { it.toInt() }
        if(t == 1) {
            a.add(x)
        } else {
            println(a.reversed()[x-1])
        }
    }
}

C - Divide and Divide

この記号が床関数と天井関数なのは知っていましたが、どういう意味だったかの知識は曖昧だったので調べるところから始めました。

それで、愚直に考えると $x$ から $⌊\frac{x}{2}⌋$ と $⌈\frac{x}{2}⌉$ の2つの数値が生まれて、生まれたやつに対してまた床関数と天井関数をとって…を1になるまで続けるわけです。これはいかにも再帰という感じがしました。愚直にというか、制約は大きく見えるけどどんどん半分になっていくので実はそんなに計算量は多くないようにも思えました。
しかし、実際に再帰で書いただけだとサンプル2まではOKだったのですがサンプル3で結果が返ってこず。そこでメモ化することを考えました。個別の結果としては $x$ が決まれば結果も決まるので、計算の過程で同じ $x$ が登場した場合は、以前辿って求めた値と必ず同じ結果になります。なので一度結果を求めた $x$ については結果をキャッシュしておくことで高速化できるだろうと。
やってみたらサンプル3もすぐに結果が返ってきたので思惑通りでした。

fun main() {
    val n = readln().toLong()

    val ans = rec(n)

    println(ans)
}

val memo = mutableMapOf<Long, Long>()

fun rec(x: Long): Long {
    val floor = x.floor()
    val ceil = x.ceil()

    if(x in memo) {
        return memo[x]!!
    }

    var ret = x

    if(floor != 1L) {
        ret += rec(floor)
    }
    if(ceil != 1L) {
        ret += rec(ceil)
    }

    memo[x] = ret

    return ret
}


fun Long.floor(): Long {
    return this / 2L
}

fun Long.ceil(): Long {
    return if(this % 2 == 0L) {
        this / 2L
    } else {
        this / 2L + 1
    }
}

ちなみに再帰でできそうというのは直感的に思ったことですが、なぜ再帰でできるのかともう少し考えてみて、 $x$ と $⌊\frac{x}{2}⌋$ および $⌈\frac{x}{2}⌉$ の関係は二分木として表現できるとわかってしっくりきました。
$N$ が15だとしたら以下のような感じになります。（2の子はどちらも1なので省略しています）

こういう木は再帰で辿れます。青丸の数値を全部足した値が答えなので、辿りながら足していけばいいわけですね。4が3つありますが、4以下の合計値は8と決まっているので、辿るのは最初の1回だけで、2回目以降はキャッシュを参照することで無駄な探索を避けられます。

D - Super Takahashi Bros.

すごくDPっぽさを感じたのでその方向で考えてみたのですが、どうもうまくいかなさそう。ステージ1への最短時間は明らかに0秒なのでそれはいいのですが、そこからステージ2までの最短時間が単純に $A_1$ かというとそうとも限らなさそう。どうやらステージ3以降からステージ2に戻るというルートもあり得るっぽいので。
仮にステージ2へ行くためにステージ1から行くルートとステージ3から行くルートの2つがあるとしたら、ステージ2への最短時間を求めるにはステージ3への最短時間が既に判明している必要があります。しかし、そうなるとステージ3へのルート全部について事前に調べる必要があります。とてもじゃないが単純なDPで解けるようなものではないとわかりました…

ここで、ステージ間のルートをグラフとして表現できることに気づきました。ステージ $N$ 以外の頂点については出次数2の有向重み付きグラフです。重みはもちろん所要時間です。

サンプル1だとこんな感じのグラフになります。

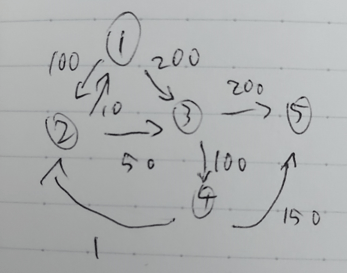
なので、単純に1から $N$ までの最短経路を求める問題ってことですね。
（重み付きグラフの場合、最短経路とは経由する辺の数が最小の経路のことではなく、重みの合計が最小の経路のことを言います。鉄則本にそう書いてありました）

最短経路といえばBFSというイメージですが、重み付きグラフの場合はダイクストラ法を使うのがよいとググってみてわかりました。ダイクストラは名前は知っているけど書いたことはないです。ただ、この問題はシンプルに最短経路を求めるだけなので、おそらくダイクストラやるだけの問題であることは想像できました。それなら既存の実装をお借りすればできるんじゃないかなあと思って、既存の実装を借りて書いたのがこちら。

import java.util.*

fun main() {
    val n = readln().toInt()

    val graph = Array(n + 1) { mutableListOf<Edge>() }
    repeat(n - 1) {
        val (a, b, x) = readln().split(" ").map { it.toLong() }

        val v = it + 1
        graph[v].add(Edge(v + 1, a))
        graph[v].add(Edge(x.toInt(), b))
    }

    val dist = dijkstra(graph, 1)
    println(dist[n])
}

// グラフを表すデータクラス
data class Edge(val to: Int, val cost: Long)

// グラフを表す型
typealias Graph = Array<MutableList<Edge>>

// 最短距離を計算する関数
fun dijkstra(graph: Graph, start: Int): List<Long> {
    val n = graph.size
    val distances = MutableList(n) { Long.MAX_VALUE }
    distances[start] = 0L

    // 優先度付きキュー
    val pq = PriorityQueue<Pair<Long, Int>>(compareBy { it.first })

    // スタートノードを追加
    pq.add(Pair(0L, start))

    while (pq.isNotEmpty()) {
        val (distance, v) = pq.poll()

        // 既に探索済みの場合はスキップ
        if (distances[v] < distance) continue

        // 隣接頂点への距離を更新
        for (edge in graph[v]) {
            val newDistance = distance + edge.cost
            if (distances[edge.to] > newDistance) {
                distances[edge.to] = newDistance
                pq.add(Pair(newDistance, edge.to))
            }
        }
    }

    return distances
}

はい、これで通ってしまいました。ほんとにダイクストラやるだけだったー！

実装の中身はちゃんと把握していないですが、思ったよりシンプルですね。後で見てみようかな…

感想

今回はわりと満足感のある感じでしたね。実装を借りたりとかしましたが、そうすれば解けるってところまでは自力でたどり着いたのでセーフ…
直近だと他の勉強をしていて精進らしい精進ができておらず、しばらくは停滞か衰退覚悟という感じです。なので、今回のように勝ててしまうことがあったら大儲けですね。ありがたい。
ダイクストラにも触れることができたし、精進していないと言いつつもコンテストに出ることで何らかの学びは得られています。しばらくはこんな感じで少しずつ進んでいきます。
（執筆時間: 49分33秒）

A - Arithmetic Progression

B - Append

C - Divide and Divide

D - Super Takahashi Bros.

感想

Discussion