AtCoder Beginner Contest 341参加記
トヨタ自動車プログラミングコンテスト2024#2(AtCoder Beginner Contest 341)に参加したので記録を残します。
今回は3完です。A~Cまでで致命的なミスはなかったものの、Dが割と解かれていたので冷えです。
A - Print 341
最初は問題文をちゃんと読んでなくて
fun main() {
val n = readln().toInt()
val sb = StringBuilder()
for(i in 0 until n * 2 + 1) {
if(i % 2 == 0) {
sb.append(1)
} else {
sb.append(0)
}
}
println(sb)
}
B - Foreign Exchange
最初は全くわからなくて一旦飛ばしてCから解きました。Cが解けた後に戻ってきました。
よく見たら単位数として出力するのは
fun main() {
val n = readln().toInt()
val a = readln().split(" ").map { it.toLong() }
val st = List(n - 1) {
val (s, t) = readln().split(" ").map { it.toLong() }
s to t
}
val array = a.toLongArray()
for(i in 0 until n-1) {
val (s, t) = st[i]
array[i+1] += array[i] / s * t
}
println(array[n-1])
}
C - Takahashi Gets Lost
グリッドで、制約が小さく見えて、ということで全探索だろうと思いました。
計算量は
アルゴリズムとしては、出発点から実際に移動をシミュレーションして一度も海に入らなかったら答えをインクリメント、というのを全マスに対して行います。
fun main() {
val br = System.`in`.bufferedReader()
val (h, w, n) = br.readLine().split(" ").map { it.toInt() }
val t = br.readLine()
val s = Array(h) {
br.readLine()
}
val diffs = mapOf(
'U' to (-1 to 0),
'L' to (0 to -1), 'R' to (0 to 1),
'D' to (1 to 0),
)
var ans = 0
for(i in 0 until h) {
for(j in 0 until w) {
if(s[i][j] == '#') {
continue
}
// TODO
if(i == 2 && j == 4) {
"1".toInt()
}
if(i == 3 && j == 5) {
"1".toInt()
}
var success = true
var currentI = i
var currentJ = j
for(k in t.indices) {
val pair = diffs[t[k]]!!
val di = pair.first
val dj = pair.second
val ii = currentI + di
val jj = currentJ + dj
if(ii !in 0 until h) {
success = false
break
}
if(jj !in 0 until w) {
success = false
break
}
if(s[ii][jj] == '#') {
success = false
break
}
currentI = ii
currentJ = jj
}
if(success) {
ans++
}
}
}
println(ans)
}
実行時間的には思ったよりも大丈夫でした。

よく見たらデバッグ用の恥ずかしいコードが残ってる……
D - Only one of two
これは残念ながら解けず、コンテスト後に通しました。
こういう
import kotlin.math.abs
fun main() {
val (n, m, k) = readln().split(' ').map { it.toLong() }
val isOk: (Long) -> Boolean = { x ->
var count = 0L
for(i in 1L..x) {
val a = i % n == 0L
val b = i % m == 0L
if(a xor b) {
count++
}
}
count >= k
}
val ans = binarySearch(-1, Long.MAX_VALUE - 1, isOk)
println(ans)
}
fun binarySearch(minNg: Long, maxOk: Long, isOk: (Long) -> Boolean): Long {
var ng = minNg
var ok = maxOk
while(abs(ok - ng) > 1) {
val mid = (ok + ng) / 2
if(isOk(mid)) {
ok = mid
} else {
ng = mid
}
}
return ok
}
ただ、これだともちろんダメです。判定問題自体の計算量がネックとなります。これをなんとか減らす必要があるのですが、その方法がわからないまま時間切れとなりました。
なぜか、なんとか探索できないかと考えていたのですが、実際には計算で求めるのが正解だったようです。
「
文章で書くとわかりづらいですが、ベン図で書くとわかりやすいそうです。
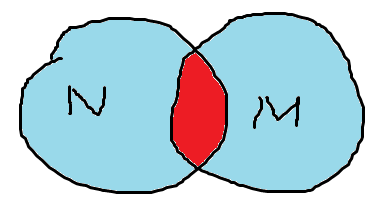
欲しいのは水色部分で、赤部分は邪魔なので引くと。なるほど。
import kotlin.math.abs
fun main() {
val (n, m, k) = readln().split(' ').map { it.toLong() }
val isOk: (Long) -> Boolean = { x ->
val count = x / n + x / m - x / lcm(n, m) * 2
count >= k
}
val ans = binarySearch(-1, Long.MAX_VALUE - 1, isOk)
println(ans)
}
fun binarySearch(minNg: Long, maxOk: Long, isOk: (Long) -> Boolean): Long {
var ng = minNg
var ok = maxOk
while(abs(ok - ng) > 1) {
val mid = (ok + ng) / 2
if(isOk(mid)) {
ok = mid
} else {
ng = mid
}
}
return ok
}
fun gcd(a: Long, b: Long): Long {
return if (b == 0L) {
a
} else {
gcd(b, a % b)
}
}
fun lcm(a: Long, b: Long): Long {
val d = gcd(a, b)
return a / d * b;
}
上限をLong.MAX_VALUE - 1としているのは、本来の上限がよくわからないので可能な限り大きな数にしたということです。本当はそれもちゃんと理解しないといけないのですが…
感想
久々に数学力で負けた気がします。数学ってほどの話じゃないかもしれないですが、最小公倍数とかベン図とか思いつきもしなくて…
そう考えると最近は数学要素が強い問題がD問題以下であんまりなかったのかな?精進できてないわりにレートが伸びていたのはそのおかげかも。
直近だと数学要素が強い問題を解いてなかったし、数学自体の勉強もできていないし、ってことでDが解けなかったのは必然的な結果でしたね。二分探索で解けるってところまではわかったので悔しいのですが。
Bの解法を思いつくのに時間がかかるとか、Cでバグらせまくって泥沼にハマるとかがなかったのでむしろよくやったほうかもしれません…w
まだしばらくは精進に時間を割けなさそうなので、当分はこんな感じが続きます。せめて爆死はしないように簡単な問題を埋めるくらいはやっていきます。
(執筆時間: 45分54秒)
Discussion