🪐

Qiskit で遊んでみる (18) — Quantum Convolutional Networks その 1

2023/08/20に公開

Python

目的

量子畳み込みニューラル・ネットワークを GPU 実装に乗せ換えようとして色々行き詰まったので、オリジナルを試してみようという内容。

量子畳み込みニューラル・ネットワーク

Cong, I., Choi, S. & Lukin, M.D. Quantum convolutional neural networks. Nat. Phys. 15, 1273–1278 (2019) で提案されたアーキテクチャ。原論文は読んでいてよく分からなくなったので、今回は忘れてしまう。使うのは

Qiskit: 量子畳み込みニューラル・ネットワーク
TensorFlow Quantum: 量子畳み込みニューラルネットワーク

の 2 つ。両方とも前述の同じ論文を参照しているので、Qiskit か Cirq かくらいの違いしかないが、恐らく、TensorFlow Quantum のほうが原論文に近い実装なのだと思われる。Qiskit のチュートリアルのほうは QCNN レイヤに 15 個のパラメータが見えるのに対し、Qiskit では

このことから、各ユニタリーは15個のパラメーターに依存しており、QCNNがHilbert空間全体をカバーするためには、我々のQCNNの各ユニタリーはそれぞれ15個のパラメーターを含んでいなければならないことがわかります。

この大量のパラメーターを調整するのは難しく、学習時間が長くなってしまいます。この問題を克服するために、私たちはansatzをヒルベルト空間の特定の部分空間に制限し、2量子ビットユニタリーゲートを $N(\alpha, \beta, \gamma)$ として定義します。これらの2量子ビットのユニタリーは[3]に見られるように、QCNNの各層で隣接するすべての量子ビットに適用されるもので、以下のようになります。

とあり、実際簡略化した実装になっている。

今回は、雰囲気を見たいだけなので Qiskit のチュートリアルの実装を使う。

今回やったこと

11_quantum_convolutional_neural_networks.ipynb を実行した。内容はチュートリアルそのままなので省略。概略としては ansatz $\ket{\psi(\theta)}$ を量子畳み込みレイヤと量子プーリングレイヤで構築して、分類器

\begin{align*} \braket{Z_7} = \braket{\psi(\theta) | Z_7 | \psi(\theta)} \in [-1, 1] \end{align*}

の期待値が -1 なら水平線、+1 なら垂直線を推定したとする二値分類である^[1]。ここで $Z_7 = I^{\otimes 6} \otimes Z$ である。

補足

事前訓練

このチュートリアルはいわゆるファインチューニングのような内容をやっている。つまり、事前訓練済みのパラメータを用いて、そこから訓練を追加実施する。

モデルの学習には長い時間がかかる可能性があるため、すでにいくつかの反復で事前学習したモデルがあり、事前学習済みの重みを保存してあります。 initial_point に学習済みの重みのベクトルを設定することで、その時点から学習を継続することにします。

とある。さて、これはどのくらいの精度のものを用いているのであろうか？

neural_network.py#L147-L170 と estimator_qnn.py#L178-L193 を参考に確認してみよう:

from qiskit.primitives import Estimator

with open("11_qcnn_initial_point.json", "r") as f:
    pretrained_params = json.load(f)

input_data = np.array(test_images)
num_samples = input_data.shape[0]
weights = np.broadcast_to(pretrained_params, (num_samples, len(pretrained_params)))
parameters = np.concatenate((input_data, weights), axis=1)

estimator = Estimator()

job = estimator.run(
    [circuit] * len(test_images),
    [observable] * len(test_images),
    parameters
)
result = job.result()
predicted_values = np.sign(result.values)
print(result.values, predicted_values)
acc = np.sum(predicted_values == test_labels) / len(test_images)
print(f"acc={np.round(acc, 2)}")

[ 0.51289937 -0.68428272 -0.28808234 0.03436394 0.529726 -0.09421202
0.16272573 -0.09746916 0.20643321 0.07950454 0.02714803 -0.22000584
0.51577936 -0.04334054 -0.36885618] [ 1. -1. -1. 1. 1. -1. 1. -1. 1. 1. 1. -1. 1. -1. -1.]
acc=0.67

0.03436394 を +1 扱いするのもどうかな？という気持ちもないわけではないが、とりあえず 0.67 という悪くない精度から始めていることが分かる。

実験結果

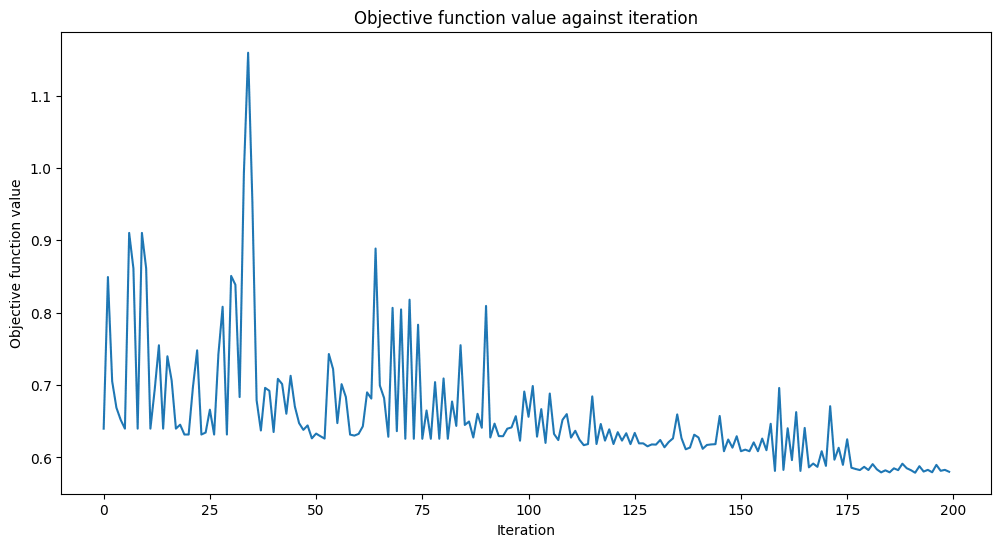
Accuracy from the train data : 91.43%
CPU times: user 2min 32s, sys: 30.3 s, total: 3min 2s
Wall time: 2min 23s

という感じでチュートリアルと似たような訓練の様子になった。

QCNNの学習には時間がかかるので、気長に待ちましょう。

と書いてあるので、かなり待たされることを覚悟したが、ファインチューニングは 2 分 30 秒弱ということになる。

評価

ノートブックのセルを逐次実行して「6. Testing our QCNN」を実行すると以下のような結果になった。

Accuracy from the test data : 80.0%

訓練済みパラメータよりは良い結果になった。

訓練済みパラメータ保存

with open("qcnn_trained_point.json", "w") as f:
    json.dump(classifier.weights.tolist(), f)

のようにすれば残しておける。

オマケ

別実装で predict を検証

API を使っているばかりだと自身がなくなってくるので、もうちょっと基本的な実装でも確認してみよう:

from qiskit.quantum_info import Statevector

expvals = []
for img in test_images:
    full_parameter = img.tolist() + classifier.weights.tolist()

    circ = circuit.bind_parameters(full_parameter)
    inv_circ = circ.inverse()
    circ.z(7)
    circ.compose(inv_circ, inplace=True)

    sv = Statevector(circ)
    expvals.append(sv[0].real)  # coefficient of |00000000>

predicted_values = np.sign(expvals)
acc = np.sum(predicted_values == test_labels) / len(test_images)
print(f"acc={np.round(acc, 2)}")

acc=0.8

で NeuralNetworkClassifier.predict と同じ結果が得られる。

スクラッチから訓練

事前訓練しない場合にはどれくらいかかるのだろうか？

random_initial_point = (np.random.rand(63) - 0.5) * np.pi / 0.5

のようなランダム値で初期化して maxiter=1000 で訓練すると以下のようになる:

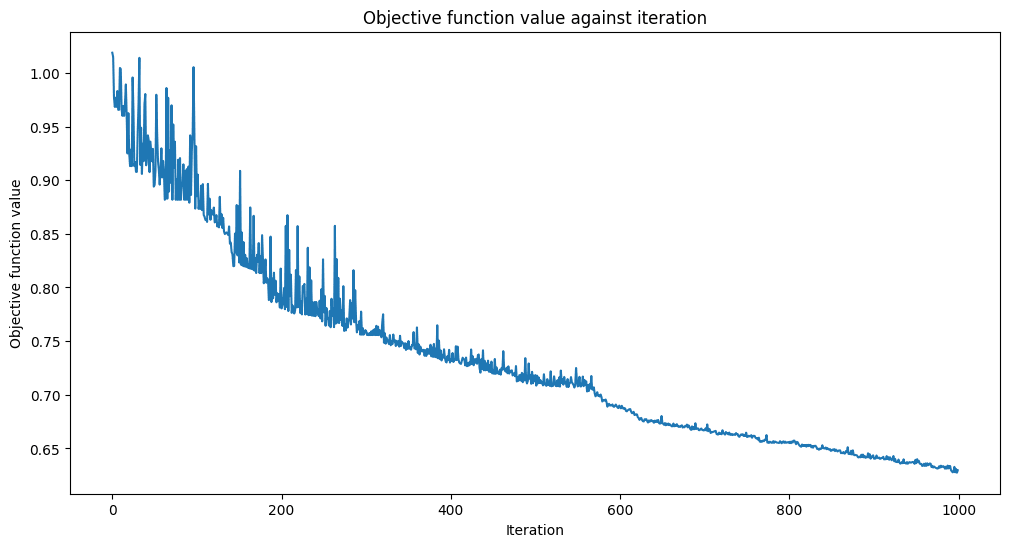
Accuracy from the train data : 77.14%
CPU times: user 12min 54s, sys: 2min 34s, total: 15min 28s
Wall time: 12min 12s

この結果、テストセットでは acc=0.8 であった。

iter=500 程度で acc=0.7、iter=1000 程度で acc=0.8 くらいになるらしい。

また使うかもしれないので、最適化後のパラメータ値も残しておく:

[2.3546402794623362, 0.46565763865242493, 0.11094331771924071, -1.6778035531433366]
[2.2289313648585347, 0.6594424460291675, -0.5432492945661821, -3.317285847097621]
[-0.3574435087896934, 2.323275959994348, 2.0309549413490537, -1.3860424443160662]
[1.6222999603417891, -1.6753977467341172, 3.411869809488068, 2.5045011300681734]
[-1.039402639233666, 1.7695128202953938, 2.061609189794608, 2.1590894499465576]
[3.636152525994555, 0.9007120879294425, -0.04687203918218217, 2.953138474889541]
[2.3637080139002906, -2.048441178272313, 0.44034719144541634, 2.638433285773038]
[-0.6595296061424282, -0.07163571288425928, -2.2129937037433423, 1.2865948147779918]
[-0.284840258530323, 2.295962679383686, -0.11187969514114203, -2.5390971426645588]
[0.7568724535683455, 0.24854824957249252, -2.350382324759061, -2.685680120590185]
[-0.7537183559803439, -2.257162215950451, 1.7463885537127504, -0.3468287868007189]
[3.104063434529963, -0.8980074282527297, 1.6609274683249684, 0.6319069397142701]
[3.0991036890351267, -2.677064254793225, 3.2022831483146104, 1.0611476681877685]
[-1.4204850218096825, 3.522995592567884, -1.472610465623983, 1.7473893112783592]
[1.8811768188320181, -1.5269413780525884, 1.7964102389080947, 3.1243979218645666]
[-0.8673817820407203, 0.0017640155478652782, -1.0958799673090145]

まとめ

ノートブックをそのまま実行しただけだが、量子畳み込みニューラル・ネットワークが少しだけ分かったような気がする。

自分でやって行き詰まる前に、既に存在するチュートリアルがある場合は、何も考えずにそれを実行するのもアリかな？と思った。

脚注

そんなに綺麗に訓練できないので、負の値なら -1 に丸め、正の値なら +1 に丸める実装になっている。 ↩︎

GitHubで編集を提案

目的