📈

行列積について考える

2022/07/24に公開

Python

math

tech

目的

行列積状態 (Matrix Product State; MPS) について理解しようと思ったらさっぱり分からなかったので、「行列積」についてちょっと分かった気になるところまでお絵描きをする。^[1]

行列積とはテンソルネットワークの一例らしい。以下の図で言うと、左のテンソルを右のように表現したものを行列積と呼ぶようである。^[2]

テンソル	の	行列積への分解
	→

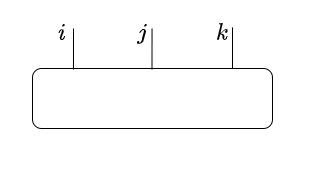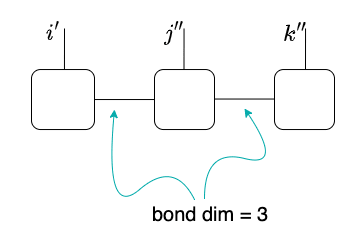文献 [2] によると「行列積」というのは行列の積ではなく多脚テンソルという説明がなされている。

このような絵を何度眺めたところで読書百遍意自ら通ずとはいかない気がするので、具体的に簡単なテンソル $T^{ijk}$ を考えてみたい。

具体例で見る行列積

3 解のテンソルを考える

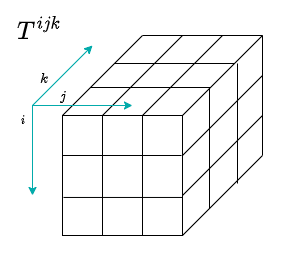
以下のような各次元が 3 であるような 3 階のテンソル $T^{ijk}$ を考える。恐らく全般に話がややこしいのは、「次元」と呼ばれるものがコンテキストによって少々異なるからであろう。

ついでに NumPy での計算例も添えていこう:

T = np.array(range(27)).reshape(3, 3, 3)
print(T)

[[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]]

[[ 9 10 11]
[12 13 14]
[15 16 17]]

[[18 19 20]
[21 22 23]
[24 25 26]]]

テンソルの添字をくくる

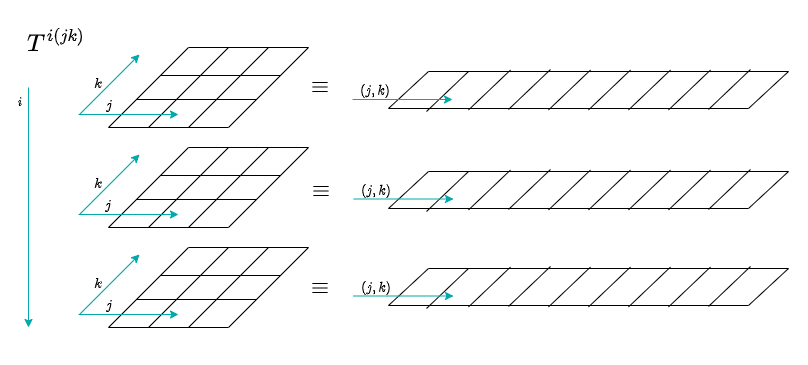
文献 [2] を参考に、 $T^{ijk}$ の添字を $i$ と $jk$ の 2 つのグループに分けてみる。図で見ると、以下のようになるだろう:

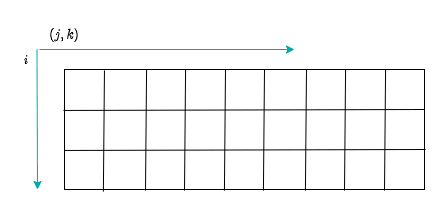
ここで $jk$ 部分は平坦にしてしまい右のように 1 解のテンソルにしてしまう。仮にこの時、 $jk$ の添字を $h = (j,k)$ にまとめてしまうとすると、 $T^{ijk}$ はテンソル $A^{ih}$ と見ることができる。

A = T.reshape(3, -1)
print(A, f'{A.shape=}')

[[ 0 1 2 3 4 5 6 7 8]
[ 9 10 11 12 13 14 15 16 17]
[18 19 20 21 22 23 24 25 26]] A.shape=(3, 9)

特異値分解を行う

先程の $A^{ih}$ を行列と見做して特異値分解すると以下のような図になる:

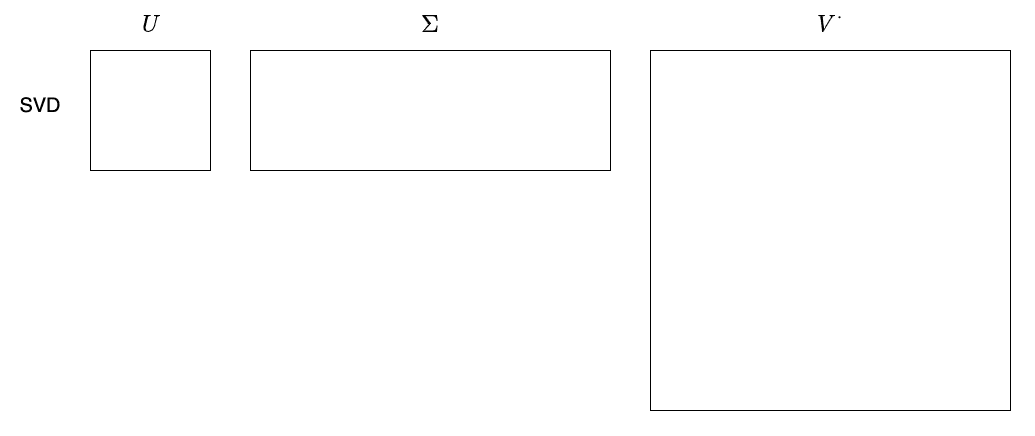
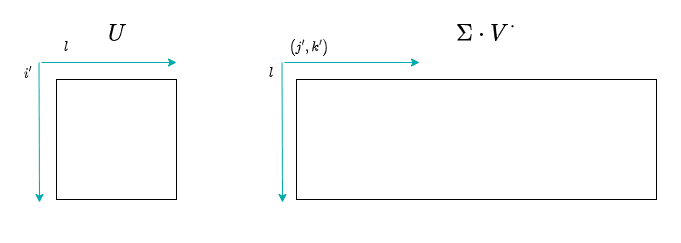
そして、 $\Sigma \cdot V^*$ の積をとってしまうと以下の図のようになる:

T1, s, vh = np.linalg.svd(A)
s = (s * np.eye(3)).flatten()
s.resize(9, 3)
s = s.T
S = (s @ vh).reshape(3, 3, 3)
print(f'{T1.shape=}, {s.shape=}, {vh.shape=}, {S.shape=}')

T1.shape=(3, 3), s.shape=(3, 9), vh.shape=(9, 9), S.shape=(3, 3, 3)

これをテンソルの絵で描くと以下のようになる:

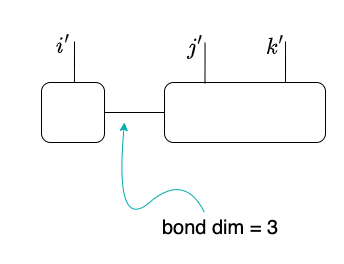
数式で書くと以下のようになるであろう:

\begin{align*} T^{ijk} = T_1^{i\ell} S^{\ell jk} \end{align*}

なお、ボンド次元については T1.shape[1] 或は S.shape[0] に現れる 3 である。

繰り返すと・・・

テンソル $S^{\ell jk}$ を $S^{(\ell j) k}$ という添字のグルーピングをして同じ手続きを実行する。すると冒頭の図になる:

Python の計算で確認する

既に T1 と S まで得ていたので、S を行列積に分解しよう。

A2 = S.reshape(-1, 3)
u2, s2, T3 = np.linalg.svd(A2)
s2 = (s2 * np.eye(3)).flatten()
s2.resize(9, 3)
T2 = (u2 @ s2).reshape(3, 3, 3)
print(f'{T1.shape=}, {T2.shape=}, {T3.shape=}')

T1.shape=(3, 3), T2.shape=(3, 3, 3), T3.shape=(3, 3)

これで、テンソル $T^{ijk}$ は行列積に分解された:

\begin{align*} T^{ijk} = T_1^{i\ell} T_2^{\ell j m} T_3^{mk} \end{align*}

検算

縮約計算を実行してみよう:

T12 = np.einsum('il,ljm', T1, T2)
T123 = np.einsum('ijm,mk', T12, T3)
print(np.round(T123, 2))

[[[ 0. 1. 2.]
[ 3. 4. 5.]
[ 6. 7. 8.]]

[[ 9. 10. 11.]
[12. 13. 14.]
[15. 16. 17.]]

[[18. 19. 20.]
[21. 22. 23.]
[24. 25. 26.]]]

最初のテンソル T が得られた。
念の為に、T1, T2, T3 を見てみると以下のようになっている:

print(np.round(T1, 2))

[[-0.17 0.9 0.41]
[-0.51 0.28 -0.82]
[-0.85 -0.34 0.41]]

print(np.round(T2, 2))

[[[-36.97 -0.44 0. ]
[-44.85 -0.07 -0. ]
[-52.73 0.3 -0. ]]

[[ -4.83 1.4 0. ]
[ -0.51 1.2 0. ]
[ 3.82 1. 0. ]]

[[ -0. -0. 0. ]
[ 0. -0. -0. ]
[ -0. -0. -0. ]]]

print(np.round(T3, 2))

[[ 0.54 0.58 0.61]
[-0.73 -0.03 0.68]
[ 0.41 -0.82 0.41]]

まとめ

結局行列積にするとどういう旨みがあるのか？とかは何も分かっていないが、どういうことをすれば行列積という形式に持ち込めるのかを簡単なサンプルで見てみた。
他の分解方法があるのか？とか一意性は？と言ったことも調べていないが、まずは一歩目ということで、残りの疑問については追々調べていきたい。

文献

[1] Matrix product state simulation method
[2] テンソルネットワークの基礎と応用
[3] Matrix Product State / Tensor Train

脚注

文献 [1], [2], [3] の順番で見ていって、何も分からんとなってしまった。 ↩︎
右の絵に要らないものがごちゃごちゃ書いてあるのは、図を使いまわしているためである。 ↩︎

GitHubで編集を提案

目的