有限差分法で微分方程式の解を眺めてみる
目的
例えば Quantum algorithm for non-homogeneous linear partial differential equations や High-precision quantum algorithms for partial differential equations のように、量子計算を活用して微分方程式を解いてみようという論文がある。ところでまったく数値解析をやったことがないこともあって、微分方程式を解くことはできても、あまり解の挙動については詳しくない。ということで、普通の数値解析、特に有限差分法で微分方程式を解いて解を可視化するということをやってみたい。
教材と概要
東海大学の遠藤先生のサイトに 世界一易しいPoisson方程式シミュレーション という、有限差分法の素晴らしい解説があったのでこれを大いに活用したい。というよりほぼこの内容を元に実装しており、可視化の際も表示について倣った。こちらの解説では熱方程式と波動方程式はカバーされていなかったので、神戸大学の陰山先生の講義資料 第2回シミュレーションスクール(H22年度後期) を拝見し、一階差分と二階差分について参考にし、熱方程式と波動方程式を実装した。
但し、数値解析の実装が実質始めてなのであまりよく分かっておらず、係数の類はそれっぽい解が得られるように調整したものもあり、境界条件の実装もあやしい。つまり、一般に参考になるような記事にはできていない。
しかしそれでも手を動かして実装し、可視化することに一定の意味があるものと考え、これを実行した。
扱う範囲
扱いが楽であるという理由で 2 次元空間
- 楕円型
- Poisson 方程式
- Laplace 方程式
- 放物型
- 熱方程式 (拡散方程式)
- 双曲型
- 波動方程式
それぞれの大雑把な特徴
楕円型
以下のような境界値問題を考える:
1 つの特性としては、この類の方程式は楕円型正則性定理により、
放物型
以下のような初期値-境界値問題を考える。
1 つの特性としては、この類の方程式は平滑化効果により、初期値
双曲型
以下のような初期値-境界値問題を考える。
1 つの特性としては、この類の方程式は解の有限伝播性により、“波の速度” に応じた速度で解の台が広がる。従って、いきなり無限遠にまで解は到達しない。
Poisson 方程式の実装
Poisson 方程式は典型的には、例えば接地した球内に配置した点電荷による静電ポテンシャルを記述する非斉次方程式である。
Laplace 方程式は Poisson 方程式において
Poisson 方程式を差分化すると大雑把には以下のようになる:
これを移項すると
となる。これを満たす函数
リンク先では正方形領域において中心に点電荷を置き、領域の正方形の境界で設置、即ち電位を 0 として解を求めている。
共通モジュールの import
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numba
from IPython.display import HTML
各種パラメータの設定と点電荷の初期化
N = 100
X = 1.0
e0 = 8.85e-12
center = np.array((N // 2, N // 2))
delta = X / N
Conv = 1.0e-6
rho = np.zeros((N, N))
for i in range(N):
for j in range(N):
if np.linalg.norm(center - (i, j))*delta < 0.05:
rho[i, j] = 1.0e-8
numba で JIT コンパイルする対象の関数定義
# Eq. (6)
@numba.jit
def calc_phi_at(i, j, phi: np.ndarray, rho: np.ndarray, e0):
return 0.25*(rho[i, j]*(delta**2)/e0+phi[i+1, j]+\
phi[i-1, j]+phi[i, j+1]+phi[i, j-1])
@numba.jit
def main_loop():
phi = np.zeros((N, N), dtype=numba.float32)
MaxPhi_list = []
loop = 0
MaxPhi = 1.0e-10
while True:
if loop%1000 == 0:
print(loop, MaxPhi)
MaxErr = CurErr = 0
for i in range(1, N-1):
for j in range(1, N-1):
Prev_phi = phi[i, j]
phi[i, j] = calc_phi_at(i, j, phi, rho, e0)
if MaxPhi < abs(phi[i, j]):
MaxPhi = phi[i, j]
CurErr = abs(phi[i, j] - Prev_phi) / MaxPhi
if MaxErr < CurErr:
MaxErr = CurErr
MaxPhi_list.append(MaxErr)
loop += 1
if MaxErr <= Conv:
return phi, MaxPhi_list
逐次近似実行
phi, _ = main_loop()
で、少し待てば解は求まる。これを可視化しよう。
可視化
静電ポテンシャルの 3 次元表示
fig, ax = plt.subplots(subplot_kw={'projection': '3d'})
xs, ys = np.meshgrid(np.arange(N), np.arange(N))
zs = phi[xs, ys]
xs_, ys_ = np.meshgrid(np.arange(N)*delta, np.arange(N)*delta)
ax.plot_surface(xs_, ys_, zs, vmin=zs.min(), cmap='viridis')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
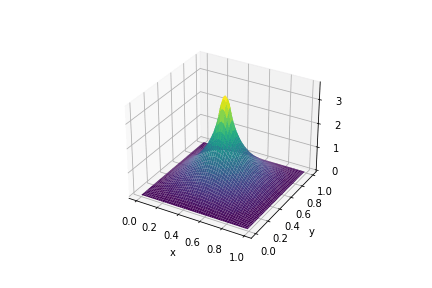
楕円型正則性定理により、十分に滑らかな解として静電ポテンシャルが求まっているようにも感じられる。
静電場と電気力線の 2 次元表示
Exs = np.zeros((N, N))
Eys = np.zeros((N, N))
Es = np.zeros((N, N))
for i in range(1, N-1):
for j in range(1, N-1):
Ex = -(phi[i+1, j]-phi[i-1, j])/(2.0*delta)
Ey = -(phi[i, j+1]-phi[i, j-1])/(2.0*delta)
Exs[i, j] = Ex
Eys[i, j] = Ey
Es[i, j] = np.linalg.norm((Ex, Ey))
fig, ax = plt.subplots(figsize=None)
xs, ys = np.meshgrid(np.arange(N), np.arange(N))
zs = Es[xs, ys]
us = Exs[xs, ys]
vs = Eys[xs, ys]
xs_, ys_ = np.meshgrid(np.arange(N)*delta, np.arange(N)*delta)
im = ax.pcolormesh(xs_,ys_,zs,vmin=np.min(zs),vmax=np.max(zs))
fig.colorbar(im, ax=ax)
ax.quiver(xs_,ys_,us,vs,linewidth=1,cmap=plt.cm.inferno,alpha=.5)
ax.set_aspect('equal')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
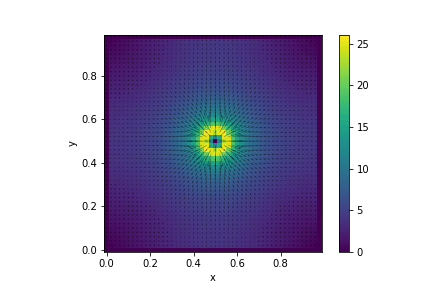
電気力線が放射状に広がるような形で電場が得られた。
Laplace 方程式の実装
Poisson 方程式のケースを応用して、Laplace 方程式を解いてみよう。今回は領域の形状を正円とし、以下のようなものを考えたい:
実はこの方程式は直接計算で解を求めることができて、
Poisson 方程式の場合との違いは境界条件の設定の部分である:
各種パラメータの設定と境界条件
thres = 0.05
@numba.jit
def init_phi(phi):
for i in range(N):
for j in range(N):
r2 = ((center[0] - i)**2 + (center[1] - j)**2)*(delta**2)
if (1 - thres)**2 <= r2 <= 1:
x_ = i - center[0]
y_ = j - center[1]
if x_ == 0:
theta = np.pi/2 if y_ >= 0 else -np.pi/2
else:
tan = y_ / x_
if x_ >= 0:
theta = np.arctan(tan)
else:
theta = np.arctan(tan) + np.pi
phi[i, j] = np.cos(3*theta)
可視化
後は Poisson 方程式と同じように解いて可視化すると以下のようになる:
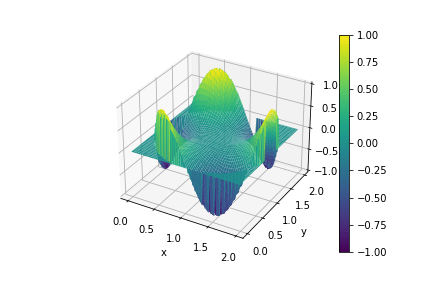
熱方程式の実装
熱方程式はその名の通り、熱が拡散する様子を記述する方程式である。
熱方程式を差分化すると大雑把には以下のようになる:
時刻
基本的な枠組みは Poisson 方程式のものを踏襲するが、ここでは点電荷であったものを「中央に集中した熱源」と読み替える。なお、
各種パラメータの設定と熱源の初期化
N = 100
X = 1.0
T = 100
k = 0.1
time_step = 5
center = np.array((N // 2, N // 2))
delta = X / N
rho = np.zeros((N, N))
for i in range(N):
for j in range(N):
if np.linalg.norm(center - (i, j))*delta < 0.05:
rho[i, j] = 10
numba で JIT コンパイルする対象の関数定義
@numba.jit
def calc_variation_at(i, j, phi: np.ndarray):
return (phi[i+1, j]+phi[i-1, j]+phi[i, j+1]+phi[i, j-1]-4*phi[i, j]) * k
@numba.jit
def calt_phi(prev_phi):
phi = np.zeros((N, N), dtype=numba.float32)
for i in range(1, N-1):
for j in range(1, N-1):
phi[i, j] = prev_phi[i, j] + calc_variation_at(i, j, prev_phi)
return phi
時間発展実行
solutions = [rho]
phi = rho
for t in range(1, T):
for _ in range(time_step):
phi = calt_phi(phi)
solutions.append(phi)
で、少し待てば各時刻ごとの解が求まる。これをアニメーションとして可視化しよう。
可視化
熱の拡散の 3 次元表示
ims = []
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for sol in solutions:
xs, ys = np.meshgrid(np.arange(N), np.arange(N))
zs = sol[xs, ys]
xs_, ys_ = np.meshgrid(np.arange(N)*delta, np.arange(N)*delta)
im = ax.plot_surface(xs_, ys_, zs, vmin=vmin, cmap='viridis')
plt.xlabel('x')
plt.ylabel('y')
ims.append([im])
ani = animation.ArtistAnimation(fig, ims, interval=100)
HTML(ani.to_jshtml())

初期値として中央に集中させた熱は時刻が進むと滑らかにじわっと広がっている様子が見える。
波動方程式の実装
波動方程式はその名の通り、波が伝播する様子を記述する方程式である。
波動方程式を差分化すると大雑把には以下のようになる:
時刻
時刻
なお、
各種パラメータの設定と波束の初期化
N = 100
X = 1.0
T = 100
c = 0.1
time_step = 5
center0 = np.array((N // 2 - 1, N // 2 - 1))
center1 = np.array((N // 2, N // 2))
delta = X / N
rho0 = np.zeros((N, N))
rho1 = np.zeros((N, N))
for i in range(N):
for j in range(N):
if np.linalg.norm(center0 - (i, j))*delta < 0.05:
rho0[i, j] = 10
for i in range(N):
for j in range(N):
if np.linalg.norm(center1 - (i, j))*delta < 0.05:
rho1[i, j] = 10
numba で JIT コンパイルする対象の関数定義
@numba.jit
def calc_variation_at(i, j, phi: np.ndarray):
return (phi[i+1, j]+phi[i-1, j]+phi[i, j+1]+phi[i, j-1]-4*phi[i, j]) * c
@numba.jit
def calt_phi(prev_phi, prev_prev_phi):
phi = np.zeros((N, N), dtype=numba.float32)
for i in range(1, N-1):
for j in range(1, N-1):
phi[i, j] = 2 * prev_phi[i, j] - prev_prev_phi[i, j] + \
calc_variation_at(i, j, prev_phi)
return phi
時間発展実行
solutions = [rho1]
prev_prev_phi = rho0
prev_phi = rho1
for t in range(1, T):
for _ in range(time_step):
phi = calt_phi(prev_phi, prev_prev_phi)
prev_prev_phi = prev_phi
prev_phi = phi
solutions.append(phi)
で、少し待てば各時刻ごとの解が求まる。これをアニメーションとして可視化しよう。
可視化
波の伝播の 2 次元表示
ims = []
fig = plt.figure()
for sol in solutions:
xs, ys = np.meshgrid(np.arange(N), np.arange(N))
zs = sol[xs, ys]
xs_, ys_ = np.meshgrid(np.arange(N)*delta, np.arange(N)*delta)
im = plt.imshow(zs, vmin=vmin, vmax=vmax, cmap='viridis')
ims.append([im])
ani = animation.ArtistAnimation(fig, ims, interval=100)
HTML(ani.to_jshtml())

波の伝播の 3 次元表示
ims = []
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for sol in solutions:
xs, ys = np.meshgrid(np.arange(N), np.arange(N))
zs = sol[xs, ys]
xs_, ys_ = np.meshgrid(np.arange(N)*delta, np.arange(N)*delta)
im = ax.plot_surface(xs_, ys_, zs, vmin=vmin, cmap='viridis')
plt.xlabel('x')
plt.ylabel('y')
ims.append([im])
ani = animation.ArtistAnimation(fig, ims, interval=100)
HTML(ani.to_jshtml())

初期値として中央に集中させた波束は時刻が進むと有限の速度で波紋が伝播していき、領域境界で反射して戻ってきた波同士の重ね合わせが発生している様子が見える。
まとめ
実装が適切かはさておき、何となく物理現象のシミュレーションを実装できたように思う。基本的な考え方は Poisson 方程式の場合を応用して実装すれば良いことも分かった。
いずれの方程式も空間変数
他のケースの方程式についても数値解析の方法が理解できたら試してみたいし、量子計算を用いた微分方程式の解法についても、手元で実装できる難易度のものであれば試してみたいと思う。
参考文献
-
この問題設定は、複素正則函数
z^3
Discussion