cuQuantum で遊んでみる (9) — 少し規模が大きめの QAOA を計算する
目的
cuQuantum で遊んでみる (8) — QAOA の期待値計算高速化 で大分計算周りをマシにしたのでもう少し本格的な計算をしてみたいというもの。
なお、今回の計算、どこか間違えているようなのだが間違えているなりにそこそこ行けてそうなので、一旦記事にしてしまって後日修正したい。 修正した[1]。再度修正した[2]。
実験は Google Colab 上で T4 を使って行った。 時間がかかるので、途中からは A100@GCP を使った。とは言え、Google Colab 上で T4 でも可能なので、そんな手軽な環境で本格的な QAOA も VQE も実行できるのである。
お題
TYTANSDK のチュートリアル 線形回帰 を拝借したい。因みにこの問題は疑似量子アニーリングで計算したらすぐに結果が得られる。
QAOA に書き直す
必要なモジュールを import する。
from __future__ import annotations
from collections.abc import Callable, Sequence
import matplotlib.pyplot as plt
from tytan import symbols_list, Compile, Auto_array
import numpy as np
from scipy.optimize import minimize
from qiskit import QuantumCircuit
from qiskit.quantum_info import SparsePauliOp
from qiskit.circuit import ParameterVector
from qiskit.circuit.library import QAOAAnsatz
from qiskit.quantum_info import SparsePauliOp
from qiskit_aer import AerSimulator
import cupy as cp
from cuquantum import CircuitToEinsum, contract
また、Rx_Rxdag などの関数は cuQuantum で遊んでみる (8) — QAOA の期待値計算高速化 の通りとする。
QUBO 定式化
線形回帰 の内容を QUBO で定式化する。
n_qubits = 16
q0, q1, q2, q3, q4, q5, q6, q7, q8, q9, q10, q11, q12, q13, q14, q15 = \
symbols_list(n_qubits, "q{}")
a = 10 + 10 * ((128*q0 + 64*q1 + 32*q2 + 16*q3 + 8*q4 + 4*q5 + 2*q6 + q7) / 256)
b = 0 + 1 * ((128*q8 + 64*q9 + 32*q10 + 16*q11 + 8*q12 + 4*q13 + 2*q14 + q15) / 256)
H = 0
H += (5.75 - (a*0.31 + b))**2
H += (8.56 - (a*0.4 + b))**2
H += (8.42 - (a*0.47 + b))**2
H += (7.78 - (a*0.4 + b))**2
H += (10.25 - (a*0.54 + b))**2
H += (6.79 - (a*0.36 + b))**2
H += (11.51 - (a*0.56 + b))**2
H += (7.66 - (a*0.43 + b))**2
H += (6.99 - (a*0.32 + b))**2
H += (10.61 - (a*0.6 + b))**2
qubo, offset = Compile(H).get_qubo()
この後、
を用いて、イジング変数で書き直す。単に面倒くさいだけで qubo 辞書の内容を ising_dict 辞書に置き換えている。
ising_dict = {}
additional_offset = 0
for k, v in qubo.items():
left, right = k
ln = int(left[1:])
rn = int(right[1:])
if rn < ln:
ln, rn = rn, ln
if ln == rn:
new_k = (f"z{ln}",)
ising_dict.setdefault(new_k, 0.0)
ising_dict[new_k] += -v/2
additional_offset += 1/2
else:
new_k = (f"z{ln}", f"z{rn}")
ising_dict.setdefault(new_k, 0.0)
ising_dict[new_k] += v/4
new_k = (f"z{ln}",)
ising_dict.setdefault(new_k, 0.0)
ising_dict[new_k] += -v/4
new_k = (f"z{rn}",)
ising_dict.setdefault(new_k, 0.0)
ising_dict[new_k] += -v/4
additional_offset += 1/4
def calc_key(k: tuple[int] | tuple[int, int]):
if len(k) == 1:
left = k[0]
ln = int(left[1:])
return 256*ln - 1
else:
left, right = k
ln = int(left[1:])
rn = int(right[1:])
return 256*ln + 16*rn
ising_dict = dict(sorted(ising_dict.items(), key=lambda k_v: calc_key(k_v[0])))
#for k in ising_dict:
# print(k)
#print(additional_offset)
#for k, v in ising_dict.items():
# k = str(k)
# n_pad = 15 - len(k)
# print(k, " "*n_pad, round(v, 5))
QAOA 回路実装
この辺は cuQuantum で遊んでみる (6) — 最大カット問題と QUBO と QAOA と同様である。
n_reps = 5
def rzz(qc, theta, qubit1, qubit2):
qc.cx(qubit1, qubit2)
qc.rz(theta, qubit2)
qc.cx(qubit1, qubit2)
betas = ParameterVector("β", n_reps)
beta_idx = iter(range(n_reps))
def bi():
return next(beta_idx)
gammas = ParameterVector("γ", n_reps)
gamma_idx = iter(range(n_reps))
def gi():
return next(gamma_idx)
qc = QuantumCircuit(n_qubits)
qc.h(qc.qregs[0][:])
for _ in range(n_reps):
gamma = gammas[gi()]
param_names.append(gamma.name)
for k in ising_dict:
if len(k) == 1:
left = k[0]
ln = int(left[1:])
qc.rz(gamma, ln)
else:
left, right = k
ln = int(left[1:])
rn = int(right[1:])
assert ln <= rn
rzz(qc, gamma, ln, rn)
qc.barrier()
beta = betas[bi()]
param_names.append(beta.name)
for i in range(n_qubits):
qc.rx(beta, i)
#qc.draw()
テンソルネットワーク実装
cuQuantum で遊んでみる (7) — 期待値計算再考 で触れた高速計算用のハミルトニアンを作成する。
I = cp.eye(2, dtype=complex)
Z = cp.array([
[1, 0],
[0, -1]
], dtype=complex)
def to_hamiltonian(ising_dict):
hamiltonian = []
for i in range(n_qubits):
row = []
for k in ising_dict.keys():
if len(k) == 1:
left = k[0]
ln = int(left[1:])
rn = None
else:
left, right = k
ln = int(left[1:])
rn = int(right[1:])
if ln == i or rn == i:
row.append(Z)
else:
row.append(I)
hamiltonian.append(cp.array(row))
return hamiltonian
hamiltonian = to_hamiltonian(ising_dict)
# 今回のハミルトニアンはごちゃごちゃした係数を持っている。
coefficients = np.array(list(ising_dict.values()))
# パラメータの bind 時に 2π を何周もする可能性があるので係数をスケールしておく。
coefficients /= np.max(abs(coefficients))
量子回路にダミーのハミルトニアンを与えて一旦、cuTensorNet のテンソルネットワークに変換してからハミルトニアンを差し替える。やや回路が深いので計算に少し時間がかかる。
%%time
dummy_hamiltonian = "Z" * n_qubits
expr, operands, pname2locs = circuit_to_einsum_expectation(qc, dummy_hamiltonian)
hamiltonian_locs = find_dummy_hamiltonian(operands)
es = expr.split("->")[0].split(",")
for loc in hamiltonian_locs:
es[loc] = "食" + es[loc]
expr = ",".join(es) + "->食"
for ham, locs in zip(hamiltonian, hamiltonian_locs):
operands[locs] = ham
CPU times: user 3.68 s, sys: 293 ms, total: 3.97 s
Wall time: 3.97 s
expr の中身が酷くて、眺めてみると面白い。「食 (hamu)」の部分にハミルトニアンを埋め込んでいる。

コスト関数を定義する。ここは見た目上は厳密ではない。問題ハミルトニアンを replace_pauli の中に隠蔽しているのであるが、その詳細を書き出すと大変煩雑になるので割愛する。
param_names = [p.name for p in qc.parameters]
losses = []
def comnpute_expectation_tn(params, *args):
expr, operands, pname2locs = args
energy = 0.
pname2theta = dict(zip(param_names, params))
# この中で、ハミルトニアンの係数を位相にかける処理も一緒にやっている。
parameterized_operands = replace_pauli(operands, pname2theta, pname2locs)
# 純粋な期待値と係数のアダマール積をとって加算する。
energy = np.sum(
cp.asnumpy(contract(expr, *parameterized_operands).real) * coefficients
)
losses.append(energy)
return energy
最適化を回す
適当な "maxiter" で回す。
%%time
init = np.random.randn(qc.num_parameters) * 2*np.pi
result = minimize(
comnpute_expectation_tn,
init,
args=(expr, operands, pname2locs),
method="COBYLA",
options={
"maxiter": 500
},
)
print(result.message)
print(f"opt value={round(result.fun, 3)}")
Maximum number of function evaluations has been exceeded.
opt value=-0.508
CPU times: user 1h 8min 56s, sys: 2min 31s, total: 1h 11min 27s
Wall time: 1h 11min 26s
(A100 でやったが) 結構時間がかかったが、まだ常識的な範囲ではあろう。そろそろ途中経過の可視化を考えたほうが良い。コールバックから値を引っ張ってきて動的にグラフを書かせるか、TensorBoard を使うといったところか。
結果を考察する
そこそこの規模だとメモリを圧迫するので、念のため AerSimulator をテンソルネットワークをバックエンドにして実行する[3]。今回のケースは shots を大きくしてもわりとすぐに完了する。理由はよく分かっていない。
%%time
def to_pauli_strings(hamiltonian: tuple[list[cp.ndarray]]):
I = cp.eye(2, dtype=complex)
Z = cp.array([[1, 0], [0, -1]], dtype=complex)
pauli_strings: list[str] = []
for ham in zip(*hamiltonian):
pauli_str = ""
for h in ham:
if cp.allclose(h, I):
pauli_str += "I"
elif cp.allclose(h, Z):
pauli_str += "Z"
else:
raise ValueError(f"{h} must be I or Z.")
pauli_strings.append(pauli_str)
return pauli_strings
qubit_op = SparsePauliOp(
to_pauli_strings(hamiltonian),
coefficients,
)
initial_state_circuit = QuantumCircuit(n_qubits)
initial_state_circuit.h(qc.qregs[0][:])
ansatz = QAOAAnsatz(
cost_operator=qubit_op,
reps=n_reps,
initial_state=initial_state_circuit,
name='QAOA',
flatten=True,
)
# パラメータを Qiskit の回路の変数に割り当てるための関数
mapping = make_pname2theta(result.x)
parameter2value = {param: mapping[param.name] for param in ansatz.parameters}
opt_ansatz = ansatz.bind_parameters(parameter2value)
opt_ansatz.measure_all()
sim = AerSimulator(device="GPU", method="tensor_network")
t_qc = transpile(opt_ansatz, backend=sim)
counts = sim.run(t_qc, shots=1024*50).result().get_counts()
CPU times: user 49.9 s, sys: 7.04 s, total: 56.9 s
Wall time: 27.5 s
Qiskit は右が LSB なので、左を LSB にする形で上位 20 の結果を表示してみる。
topk = 20
states = []
for i, (k, n) in enumerate(sorted(counts.items(), key=lambda k_v: -k_v[1])):
if n < 5:
continue
state = k[::-1] # reverse order
print(f"[{i:02}] {state} {n}")
states.append(state)
i += 1
if i >= topk:
break
[00] 1100111110111111 50
[01] 1001111101111111 37
[02] 1100111110111110 36
[03] 1101111101111111 36
[04] 1010111110111101 34
[05] 1001111101111010 34
[06] 1110111100111111 33
[07] 1101111101111110 32
[08] 0010111100111111 32
[09] 1101111101111100 32
[10] 1010111110111110 30
[11] 1100111110111101 30
[12] 1010111110111111 30
[13] 0010111100111110 29
[14] 1001110101111111 29
[15] 1110111100111110 28
[16] 1001111001111101 28
[17] 1001111101111100 28
[18] 1001111001111110 28
[19] 1010111110111011 28
線形回帰の係数を求める関数。
def calc_ab(state: str):
q0, q1, q2, q3, q4, q5, q6, q7, q8, q9, q10, q11, q12, q13, q14, q15 = [int(c)
for c in state]
a = 10 + 10 * ((128*q0 + 64*q1 + 32*q2 + 16*q3 + 8*q4 + 4*q5 + 2*q6 + q7) / 256)
b = 0 + 1 * ((128*q8 + 64*q9 + 32*q10 + 16*q11 + 8*q12 + 4*q13 + 2*q14 + q15) / 256)
return a, b
線形回帰のグラフを描く
ビリリダマ 10 匹のデータ:
bibiridama = np.array([
[0.31, 5.75],
[0.4, 8.56],
[0.47, 8.42],
[0.4, 7.78],
[0.54, 10.25],
[0.36, 6.79],
[0.56, 11.51],
[0.43, 7.66],
[0.32, 6.99],
[0.6, 10.61],
])
グラフに描き出す。これが面白いくらい妥当な見栄えになっている。
xs = bibiridama[:, 0]
ys = bibiridama[:, 1]
plt.figure()
plt.scatter(xs, ys)
print(states[0])
a_, b_ = calc_ab(states[0])
print(a_, b_)
x = np.arange(0.3, 0.6, 0.01)
y = a_*x + b_
plt.plot(x, y, color="red")
plt.show()
1100111110111111
a = 18.0859375
b = 0.74609375
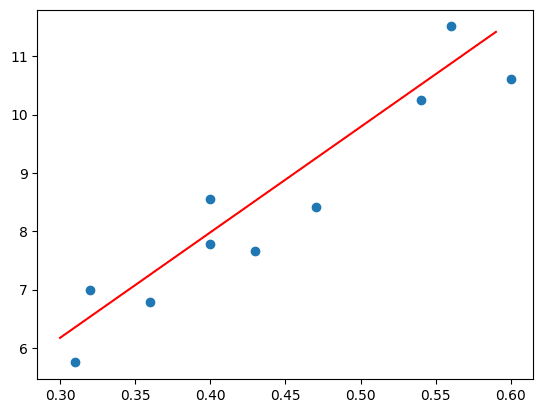
2~3 番目の解でも同じようなグラフになっている。TYTANSDK のチュートリアルで疑似量子アニーリングで求める場合、
a = 17.1875
b = 0.88671875
らしいので、そこそこ良さそうである。
最後にコストの動きも見てみよう。
plt.figure()
x = np.arange(0, len(losses), 1)
plt.plot(x, losses, color="blue")
plt.show()

まとめ
疑似量子アニーリングの題材を使って 16 量子ビットの QAOA を実行してみた。
解の候補一覧から分かることだが、16 量子ビット程度の QAOA で既に最適解の確率振幅は驚く程小さい。僅差でトップになっているに過ぎない。Deutsch-Jozsa のアルゴリズムや Grover のアルゴリズムといった FTQC 用の解の絞り込みが工夫されたちゃんとしたアルゴリズムと異なり、NISQ 向けのメタヒューリスティクスなので仕方ない部分もあるかもしれないのだが、かなり大らかな気持ちで「解に近いものが得られたら御の字」くらいでやらないと厳しいのかもしれない。
Discussion