🪐

cuQuantum で遊んでみる (2) — グローバー探索アルゴリズム

2022/11/01に公開

Python

目的

引き続き cuQuantum で遊んでみたい。適当な題材が思いつかないので、Qiskit で遊んでみる (4) を元にグローバー探索アルゴリズムを実行したみたい。

コンテンツ

Qiskit で遊んでみる (4) に対応させる形で用意した、GitHub のこちらをそのまま利用する。

解説はすべて前回の記事に譲ることにして、今回も 2 つの解を持つオラクルを作成して探索を実行する。

基本的な回路（オラクル/Diffuser）の実装

基本的なパッケージのインポート

まずは基本的なパッケージをインポートする。cuQuantum を使うのだが、デフォルトのバックエンド CuPy を使うので、併せてインポートする。

import numpy as np
import cupy as cp
from qiskit import QuantumCircuit, QuantumRegister
from qiskit.circuit.library import MCXGate
from cuquantum import CircuitToEinsum, contract
%matplotlib inline

オラクルの作成

そのままコピペでオラクルの回路を用意する。前回は力押しでマルチ制御ゲートを実装したが、そんな対応は不要でパウリゲートの関係 $HXH = Z$ を考慮すれば、複数の制御ビットを持つような $Z$ ゲートは簡単に定義できる。このために、複数の制御ビットを持つような $X$ ゲート MCXGate をインポートした。

def revserse_phase(qc: QuantumCircuit, state: str):
    qubits = []
    for i, digit in enumerate(state[::-1]):
        if digit == '0':
            qubits.append(i)
    if qubits:
        qc.x(qubits)
    # MCZ start (HXH = Z)
    qc.h(n_qubits - 1)
    qc.append(MCXGate(n_qubits - 1), list(range(n_qubits)))
    qc.h(n_qubits - 1)
    # MCZ end
    if qubits:
        qc.x(qubits)

def define_oracle(solutions):
    # Create the oracle
    qreg = QuantumRegister(n_qubits, 'qr')
    oracle = QuantumCircuit(qreg)

    for sol in solutions:
        revserse_phase(oracle, sol)

    return oracle

Diffuser の作成

続けて diffuser と呼ばれる回路を定義する:

def define_diffuser(n_qubits):
    qreg = QuantumRegister(n_qubits, 'qr')
    diffuser = QuantumCircuit(qreg)
    diffuser.h(qreg[:])
    diffuser.x(qreg[:])
    # MCZ start (HXH = Z)
    diffuser.h(qreg[n_qubits - 1])
    diffuser.append(MCXGate(n_qubits - 1), list(range(n_qubits)))
    diffuser.h(qreg[n_qubits - 1])
    # MCZ end
    diffuser.x(qreg[:])
    diffuser.h(qreg[:])

    return diffuser

5 量子ビットに挑戦！

今回の問題では 5 桁の 2 進数で解は 00101 と 11111 の 2 つとしてみた。まずは一応回路を可視化して確認しておきたい。

n_qubits = 5
solutions = ['00101', '11111']

oracle = define_oracle(solutions)
oracle.draw('mpl')

diffuser = define_diffuser(n_qubits)
diffuser.draw('mpl')

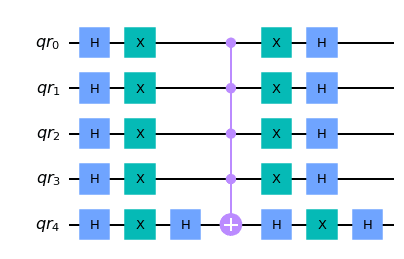
良さそう。

とりあえず解いてみる

N = 2**n_qubits
angle = np.arcsin(np.sqrt(len(solutions) / N))
counts = int((np.pi/2 - angle) / (2*angle) + 0.5)
print(f'{angle=}, {np.pi/2=}, {counts=}')

angle=0.25268025514207865, np.pi/2=1.5707963267948966, counts=3

なので、3 回くらいアルゴリズムを反復すると、解に対応する確率振幅が最大になっているはずである。

qreg = QuantumRegister(n_qubits, 'qr')
grover = QuantumCircuit(qreg)
# initialize |s>
grover.h(qreg[:])
for _ in range(counts):
    grover = grover.compose(oracle)
    grover = grover.compose(diffuser)
grover.draw('mpl')

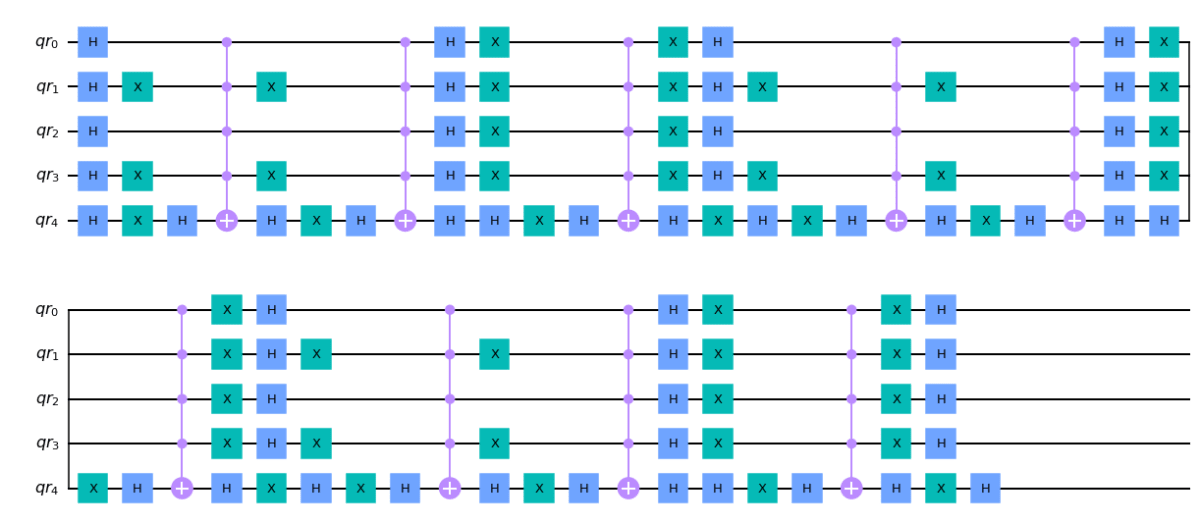
ちょっと見たくない感じの回路になってしまった・・・。

Qiskit の状態ベクトルシミュレータで解く

from qiskit import transpile
from qiskit.tools.visualization import plot_histogram
from qiskit_aer import AerSimulator

qc = grover.copy()
qc.measure_all()
sim = AerSimulator()
transpiled_grover = transpile(qc, backend=sim)

result = sim.run(transpiled_grover).result()
print(result.get_counts())
plot_histogram(result.get_counts())

より、解 00101 と 11111 の確率振幅が極めて大きくなっているのが分かる。

cuQuantum の状態ベクトルでも解いてみる

cuQuantum の .state_vector() メソッドを使ってみる。LSB が左、MSB が右になっているように見えたので、“反転処理” を入れた。公式ドキュメント cuquantum.CircuitToEinsum を見た感じではこの対応は不要そうにも感じるのだが、今すぐはよく分からない・・・。

from qiskit_aer.quantum_info import AerStatevector

converter = CircuitToEinsum(grover.decompose())
expr, operands = converter.state_vector()
sv = contract(expr, *operands)
sv = cp.asnumpy(sv)

# LSB が表示状右になるようにリストの中身を詰め替える
sv = sv.ravel()
state_map = {i: int(format(i, '05b')[::-1], 2) for i in range(N)}
sv2 = np.zeros_like(sv)
for i, j in state_map.items():
    sv2[i] = sv[j]

AerStatevector(sv2).draw('latex')

$0.035907766232 |00000\rangle+0.035907766232 |00001\rangle+0.035907766232 |00010\rangle+0.035907766232 |00011\rangle+0.035907766232 |00100\rangle-0.693296101866 |00101\rangle + \ldots +0.035907766232 |11011\rangle+0.035907766232 |11100\rangle+0.035907766232 |11101\rangle+0.035907766232 |11110\rangle-0.693296101866 |11111\rangle$

ということで、 $\ket{00101}$ と $\ket{11111}$ の振幅が大きいことが分かる。

7 量子ビットに挑戦！

もう回路の可視化や状態ベクトルはつらいので、確率振幅を直接求めることにする。

.decompose() を連打しているのは都合であって本質的なものではない^[1]。ちなみに今回はアルゴリズムの反復回数は counts = 6 である。

n_qubits = 7
solutions = ['1011011', '1111111']

N = 2**n_qubits
angle = np.arcsin(np.sqrt(len(solutions) / N))
counts = int((np.pi/2 - angle) / (2*angle) + 0.5)

oracle = define_oracle(solutions)
diffuser = define_diffuser(n_qubits)

qreg = QuantumRegister(n_qubits, 'qr')
grover = QuantumCircuit(qreg)
# initialize |s>
grover.h(qreg[:])
for _ in range(counts):
    grover = grover.compose(oracle)
    grover = grover.compose(diffuser)
grover = grover.decompose().decompose().decompose()

さて、以下で探索を実行するが、実際にはズルをしている。全ケースの探索をしていられないので、ハズレのケース ( $\ket{0000000}$ ) と解のケースを求めてみている。

bitstring は cuQuantum としては “LSB が左、MSB が右になっているように見えた” ので反転して入力している。

converter = CircuitToEinsum(grover)

for bitstring in ['0000000'] + solutions:
    expr, operands = converter.amplitude(bitstring=bitstring[::-1])
    amplitude = contract(expr, *operands)
    print(bitstring, amplitude)

0000000 (-0.005205551991224629+4.900878915069496e-16j)
1011011 (0.7058986048954989-1.0778748759672516e-14j)
1111111 (0.7058986048955004-1.2457685223367046e-14j)

明らかに解のケースで確率振幅が大きくなっているのが見て取れると思う^[2]。

まとめ

少し無理矢理感はあったが、cuQuantum を使ってグローバー探索アルゴリズムを実行してみた。実際の使い方としてどういった使い方が良いのか分からないので、とりあえず使ってみた程度なのだが、もっと情報を集めて実用的な内容を試していきたい。

脚注

ある程度分解しておかないと CircuitToEinsum が期待しているメソッドを持った単純なゲートだけで構成されてくれないのである・・・。 ↩︎
GPU は T4 を使ったが、この 3 つの確率振幅の計算はちょっと時間がかかって、6 分くらいかかった・・・。つまり、1 つの振幅の計算に 2 分かかってしまった。もっとうまく使えば速度向上が見込めるのだろうか？ ↩︎

GitHubで編集を提案

目的