バイアス-バリアンスについて考える (1)

目的

色々思うところがあって^[1]、たまには Pattern Recognition and Machine Learning を読んでバイアスとバリアンスについて思いを馳せてみようという企画。読書メモとも言う。

今回の範囲

PRML 1.5.5 Loss functions for regression (pp.46-47) を眺める。この内容は推定問題について神様的な視点で全体を見渡した時の話で、関係する世界中のデータをかき集めてきた時にどういった事が言えるか？を評価するものである。

課題

あるラベル付きのデータセットが与えられた時に、データからラベルを推定する最良のモデルを構築したい。この時、バイアスやバリアンスの視点でモデルを取り巻く状況を数理的にとらえたい。前提として、データセットの規模に制限はなく望めば世界中、過去も未来のデータさえも得られるものとする。

バイアスとバリアンス

このコンテキストで言う “バイアス” はニューラルネットの線形層に出てくる $b = (b_1, \cdots, b_n)^T$ みたいなやつではなく、モデルがそれを説明したい実データの集団の中央線をどれだけ通ることができているか？という指標みたいなものである。学習ができていない場合、全然説明できていないため、集団の中央を通ることは期待できず、いわゆるアンダーフィッティング状態にある。Kaggle に投稿されている Theoretical ML Interview Question: Bias-Variance Tradeoff にあるようなダーツの的のような絵はよく見るが、分かるような分からないような部分がある。

そこで、賃貸の条件（データ; 特徴量）と賃料（ラベル）の擬似的なデータセットを作って考察をしてみたい。

賃貸の条件と賃料の擬似的なデータセット

主観で作ったものだが、以下のようなデータセットを考えてみたい。1 部屋なら 家賃 3.5 万円、2 部屋なら 5 万円、3 部屋なら8 万円、4 部屋なら 11 万円くらいにしてみて、駅から遠いとか築年数が相当経っているなら少しお安くするみたいな気持ちで適当に作ったものである。

import numpy as np
from dataclasses import dataclass

@dataclass
class Condition:
    distance: int # minutes on foot from the station
    rooms: int # number of rooms
    age: int

datasets = np.array([
    (Condition(5,1,20),3.5),(Condition(10,1,30),3),  (Condition(10,2,15),5),
    (Condition(5,1,20),3.5),(Condition(20,3,40),6.8),(Condition(15,1,10),3.4),
    (Condition(7,2,5),5),   (Condition(7,3,20),8),   (Condition(3,1,5),3.5),
    (Condition(15,4,25),10.8),(Condition(20,3,40),6.8),(Condition(10,2,15),5),
    (Condition(20,1,15),3.3),(Condition(5,2,10),5),  (Condition(3,1,40),3)
])

これを部屋数と家賃について 2D で可視化すると以下のようになる。都合良く作ったデータセットなので以下にも線形回帰しやすそうだ。

import matplotlib.pyplot as plt

conditions = datasets[:, 0]
rents = datasets[:, 1]

key = 'rooms'
plt.scatter([getattr(c, key) for c in conditions], rents)
plt.xlabel(f'{key} (x)')
plt.ylabel('rent (t)')
plt.show()

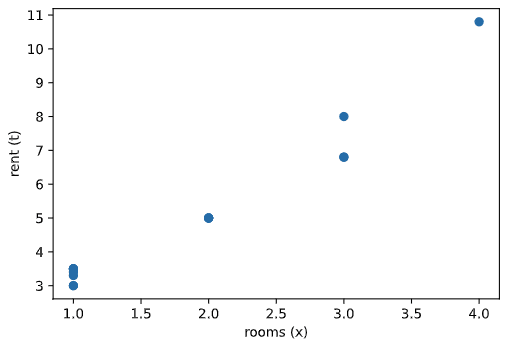
ここで $x=1$ や $x=3$ を見ると複数の $t$ 値が存在していることが分かる。家主の意向もあるだろうし、部屋数では決まらない他の条件もあるだろうし、同じ部屋数でも家賃は上下に分布する。この変は家主の意向を説明変数に落とし込めるかはあやしく、どうしてもデータセットのノイズとして残ってくる可能性がある。

この散布図では表現できていないが、同じ $t$ 値に対して $x$ 方向にも分布する。家賃 8 万円でも新築なら 1 部屋かもしれないし、あまり立地条件が良くないところなら 3 部屋ということもあるかもしれない、ということだ。要するに、$(x, t)$ は何かしら「そういう組み合わせがさもありそう」という確率分布 $p(x, t)$ で表現されることが考えられる。この例では $(x, t) = (1, 3)$ 当たりに分布の 1 つの峰があることになる。

以下では世界中のありとあらゆるデータ $\{(x_1, t_1), \cdots, (x_i, t_i), \cdots, (x_K, t_K)\}$ が集められており、完全に分布 $p(x, t)$ が分かっているという前提とする。また、説明変数 $x$ は流石に 1 つということはないであろうから、何かしらのベクトル $\mathrm{x}$ であるとする。

モデルとその理想的な姿

適当な説明変数のベクトル $\mathrm{x} = (x^1, \cdots, x^d)^T$ によって賃料を推定するような曲線（モデル） $t = y(\mathrm{x})$ を作ったとする。理想的な場合にはどういうものになるであろうか？

世界中のデータをかき集めたものは $(\mathrm{x}, t)$ 空間内に連続的に分布し、同じ $(\mathrm{x}, t)$ 値のものはまとめることで、連続確率分布 $p(\mathrm{x}, t)$ をなすと考えられる。

この確率分布のもとで、モデルの推定値と実際の賃料の 2 乗誤差 $L(t, y(\mathrm{x})) = (y(\mathrm{x}) - t)^2$ の期待値を考えてみたい:

$$\begin{align*} \mathbb{E}[L] &= \int\int L(t, y(\mathrm{x})) p(\mathrm{x}, t) d\mathrm{x} dt \\ &= \int\int (y(\mathrm{x}) - t)^2 p(\mathrm{x}, t) d\mathrm{x} dt \tag{1} \end{align*}$$

となる。^[2] これを何とかして可能な限り小さくしたいというのが課題のゴールである。果たして $0$ にできるのであろうか？

今回、$y(\cdot)$ は家賃の推定を完璧にできると嬉しいので、“作用積分” $\mathbb{E}[L]$ の極値をとるような関数であって欲しい。こういう話になると、解析力学において Euler-Lagrange 方程式を導く「変分法」の出番であり、案の定「変分法」を使う。

変分法の数学的な扱いは置いておいて、$y(\cdot)$ が極値をとっていると想定する場合からスタートする。この場合、強い信念によって、$y(\cdot)$ という関数を無限小だけ変動させても “作用積分” は極値付近で安定しているので、積分値は無限小しか変動しないと考える。^[3] 従って、この無限小の関数を $\delta y(\cdot)$ とすると、

$$\begin{align*} \int\int ((y(\mathrm{x}) + \delta y(\mathrm{x}) ) - t)^2 p(\mathrm{x}, t) d\mathrm{x} dt = \int\int (y(\mathrm{x}) - t)^2 p(\mathrm{x}, t) d\mathrm{x} dt \end{align*}$$

となる。これをまとめて累次積分の形で書くと

$$\begin{align*} 2 \int d\mathrm{x} \delta y(x) \int (y(x) -t) p(\mathrm{x}, t) dt = \int F(x) \delta y(x) d\mathrm{x} = 0 \tag{2} \end{align*}$$

を得る。ここで、$F(x) = 2 \int (y(x) -t) p(\mathrm{x}, t) dt$ である。^[4]

(2) 式で $\delta y(\cdot)$ には “任意性” があるので、積分が $0$ になるためには恒等的に $F(\mathrm{x}) = 0$ である必要がある。かくして、

$$\begin{align*} y(\mathrm{x}) = \frac{\int t p(\mathrm{x}, t) dt}{p(\mathrm{x})} = \int t p(t|\mathrm{x}) dt = \mathbb{E}_t[t|x] \tag{3} \end{align*}$$

を得る。ここで、$p(t|x) = \frac{p(\mathrm{x},t)}{p(\mathrm{x})}$ である。$y(\cdot)$ は理想的な関数の時には条件付き期待値の形で表現された。今回考えているデータセットの言葉で書くと「3 部屋の場合のお家賃の相場はお幾らでしょうか？」という関数が $y(\cdot)$ ということである。気持ち的には 8 万円ということにしていた。

PRML に倣って、何の期待値であるか？という情報 $t$ を落として、以下、$\mathbb{E}_t[t|\mathrm{x}]$ を単に $\mathbb{E}[t|\mathrm{x}]$ と書く。

理想的とは言えない一般のモデルについて何が言えるか？

理想の姿を求めたので、一般のモデル $y(\mathrm{x})$ の場合に何が言えるかを考えてみたい。

再び (1) 式に戻って、被積分関数を展開する。理想が分かったので、理想 $\mathbb{E}[t|\mathrm{x}]$ と現実 $y(\mathrm{x})$の差に注目する。次回の記事で $h(\mathrm{x}) := \mathbb{E}[t|\mathrm{x}]$ と置くので、気が早いがこの記号を使う。

$$\begin{align*} (y(\mathrm{x}) - t)^2 &= (y(\mathrm{x}) - h(\mathrm{x}))^2 + 2(y(\mathrm{x}) - h(\mathrm{x}))(h(\mathrm{x}) - t) + (h(\mathrm{x}) - t)^2 \tag{4} \end{align*}$$

であるが、(1) 式と同様に積分 $\int\int \cdots p(\mathrm{x}, t) d\mathrm{x}dt$ をとる。ここで、$\int (h(\mathrm{x}) - t) p(\mathrm{x}, t) dt = p(\mathrm{x}) \int (h(\mathrm{x}) - t) p(\mathrm{t|x}) dt = p(x) (h(\mathrm{x}) - \mathbb{E}[t|\mathrm{x}]) = 0$ を考慮すると、(4) 式の右辺第 2 項の積分は消える。よって積分を累次積分にして $dt$ を先に計算することで以下を得る:

$$\begin{align*} \mathbb{E}[L] = \int (y(\mathrm{x}) - h(\mathrm{x}))^2 p(\mathrm{x}) d\mathrm{x} + \int \operatorname{var}[t|\mathrm{x}] p(\mathrm{x}) d\mathrm{x} \tag{5} \end{align*}$$

ここで、$\operatorname{var}[t|\mathrm{x}] = \int (t - h(x))^2 p(t|\mathrm{x}) dt$ である。

前にこの推定誤差の期待値について「果たして $0$ にできるのであろうか？」というコメントをしたが、実は残念ながら一般に期待できそうにない。(4) 式の右辺第 2 項にはモデル $y(\cdot)$ が含まれておらず制御できない正の値だからである。つまり、条件が完全に同一条件の物件だとしても、家主さんの中には「できるだけ安く貸してあげたい」とか「不動産投資なんだから安くする義理などない」などの気持ちの揺らぎがあるので、まず確実にラベルは揺らいで賃料は上下に分布している。こういったデータセットのノイズである。

一方で、右辺第 1 項は制御可能であり、例えば神様なら世界中のありとあらゆる、過去と未来、時間を超えた家賃も分かるので、完璧なモデル $t = h(\mathrm{x})$ を構築できる。この時、右辺第 1 項は $0$ となる。

ところがそんなデータセットが得られるわけがないじゃないかということで、現実的には手に入るデータから家賃を推定することになる。これが次回の記事のスコープである。

まとめ

他人の褌で相撲を取っているわりには長い記事になってしまった。PRML はそれほど行間の広い本だとは思わないが、記号の意味などについて著者が自明と思っているケースでは定義が省略されるように見えるし、条件付き〇〇の類については立ち止まって意味を考えないと次第に数式が分からなくなる。ということで家賃推定モデルの言葉で書き直したり、変分法のもやもやする部分を細かく展開しているうちに長くなってしまった。

とにかく「一般には、最良のモデルであっても、予測誤差は完璧には $0$ にできない」というのがこの範囲の重要な学びであろう。これを解消するには、家主さんの気持ちすらも特徴量に組み込んで、$\mathrm{x}$ に対する多値性を排除した、完璧に完璧なデータセットを作るしかない。

脚注

1. 実務上は「ML なんて実務に耐える結果が出たら何でもいいでしょ。過学習が何？数式が何？」って態度でとりあえず訓練回して、グラフは最悪な形状だけど実際にパラメータをロードしたら「お、案外いいじゃない」となれば mission completed な気持ちで過ごしている。誰も数式に興味がないし「正規方程式を解くと」とか「このモデルの設計のポイントは」なんて話は受けが悪い。すると結果が出る話とお金になる話ばかりに頭が行ってしまう。が、毎回そうだと格好悪いことになる時も出てくるかもしれないので、PRML を読んで分かった気持ちになっておこう、ということである。

2. こう書くと急に小難しくなるが、今回は「連続確率分布 $p(\mathrm{x}, t)$ をなす」と書いたもののこれは嘘であり、離散的に決まっているので、$\frac{1}{K} \sum_{i=1}^K (y(\mathrm{x}_i) - t_i)^2$ のことである。これだと $\mathrm{x}$ と $t$ が連動しており、全空間にわたる積分 $d\mathrm{x} dt$ 感がないように見えるが、$\exist i\ \text{s.t.}\ (\mathrm{x},t) = (\mathrm{x}_i,t_i)$ 意外の $(\mathrm{x},t)$ に対してはデータが存在しないので、その点では確率密度関数が $0$ をとっていると考えれば良いのである。

3. 放物線 $y = x^2$ のお椀の底 $x=0$ 付近は平らで、$\frac{dy}{dx}|_{x=0} = 0$ なので、$0$ に無限小 $\varepsilon$ を加えた $x = 0 + \varepsilon$ という位置での値 $(0 + \varepsilon)^2$ もまた無限小であろうという哲学である。

4. $F(\mathrm{x})$ を PRML では $\frac{\delta \mathbb{E}(L)}{\delta y(\mathrm{x})}$ という記号で表現している。「$y(\mathrm{x})$」を 1 つの記号と考えて (1) 式をこれに関して形式的に “偏微分”（？）したような形になるが、こういうコンテキストでは $\partial$ ではなく $\delta$ を使うように感じる。