Diffusion Modelを理解したい。

拡散モデル

英語の方が説明が多い

Deep Unsupervised Learning using Nonequilibrium Thermodynamics（訳：非平衡熱力学を用いた深い教師なし学習）
Jascha Sohl-Dickstein, Eric A. Weiss, Niru Maheswaranathan, Surya Ganguli
12 Mar 2015

https://arxiv.org/pdf/1503.03585.pdf

diffusion modelの最初の論文

🤨🤔😑😨😱

Abstractの翻訳

機械学習における中心的な問題の一つは、学習、サンプリング、推論、評価が解析的にも計算的にも取り扱いやすい状態で、高度に柔軟な確率分布のファミリーを用いて複雑なデータセットをモデル化することです。ここでは、柔軟性と取り扱いやすさの両方を同時に達成するアプローチを開発しました。このアイデアの本質は、非平衡統計物理学に触発されて、反復的な前方拡散プロセスを通じてデータ分布の構造を系統的かつゆっくりと破壊することです。次に、データに構造を復元する逆拡散プロセスを学習し、これによりデータの高度に柔軟で取り扱いやすい生成モデルを得ます。このアプローチにより、数千層またはタイムステップを持つ深い生成モデルから迅速に学習し、サンプリングし、確率を評価することができるだけでなく、学習されたモデルの下で条件付きおよび事後確率を計算することができます。さらに、アルゴリズムのオープンソースのリファレンス実装をリリースします。

非平衡統計物理学への理解はどれぐらい必要ですか。統計力学 I, II (田崎)しか読んでないんですが戦えますか。

🤨🤔😑😨😱

非平衡統計力学の入門の講義（日本語）落ちてる。

スライドだけざーっと見たけど、解析力学と平衡統計力学は必修っぽい内容。マルコフジャンプ過程を取り扱っている。最後にランジュバン方程式を取り扱っている。拡散モデルの理解とは少しズレるかもだけど全く役にたたない訳でもないかんじする。
Part2の11ページで出てくるシャノンのエントロピーの解説とかは面白い。

🤨🤔😑😨😱

マルコフ過程の理解は必要っぽい。気体が特定の状態から平衡状態に拡散されていく際の確率モデルを理解するのに使うみたい。

KLダイバージェンスの式変形周りの理解は必要っぽい。VAEのロス関数周りの数式に似てる？

🤨🤔😑😨😱

Forward Trajectory （フォワード軌道）:

\mathbf{x}_{t+1} = \sqrt{1 - \beta_{t}} \mathbf{x}_{t} + \sqrt{\beta_{t}} \boldsymbol{\epsilon}

$\mathbf{x}_{t}$ は時間tの状態、 $\boldsymbol{\epsilon}$ は正規分布。上記の漸化式で状態に対して段々と乱雑さを加えていって、並行状態に達する。

このモデルは1 Stepごとに、系に $\beta_{t}$ の乱雑さを加えている。

このモデルを部屋の気体の拡散のモデル化に使う場合は、 $\beta_{t}$ は徐々に収束するようにモデル化されると思う。（部屋の中の気体の乱雑さには上限があるため。）
ただ、今回の場合は、徐々に増やす方向で乱雑さを加えている。そうすることで、逆プロセスにおいて収束しやすい。なぜならいきなり乱雑にならないので、画像の細部を再現できるようになる。（これは論文中のSETTING THE DIFFUSION RATE βtを読んだ時の私の理解）

🤨🤔😑😨😱

Reverse Trajectory （リバース軌道）：

微小時間の場合、リバースステップはフォワードステップと同じ関数の形になるらしい。つまりフォワード軌道がマルコフ過程だったら、リバース軌道もマルコフ過程になるそう。これは統計物理ですでに示されてるらしい。Diffusion Modelはそれを利用してるらしい。

Diffusion Modelを理解するにはマルコフ過程は必修で、非平衡の統計物理はそこまで必須じゃない気がする。（私はどちらも未履修）

🤨🤔😑😨😱

リバース軌跡って全く直感的じゃないんだけど。

フォワード軌道は、系に乱雑さを加えて、全体として正規分布に近づけていくってのはわかるんだけど。リバース軌跡は、系に調整された乱雑さを加えていって、全体として元の状態に戻るって言ってる。
そんなことある？どんなに調整しても乱雑さを加えたら系全体はより乱雑になるのでは？

🤨🤔😑😨😱

単純なモデルを考える。

フォワード軌跡

x^{0} \sim \delta (0) \\ x^{1} = \sqrt{1 - \beta} x^{0} + \sqrt{\beta} \epsilon

リバース軌跡

x^{0} = x^{1} + f_{\mu}(x^{1}) + f_{\sigma}(x^{1}) \epsilon

（論文中では $x^{1} + f_{\mu}(x^{1})$ を全部で $f_{\mu}(x^{1})$ としてるかも。）

$f_{\mu}(x^{1}) = - (x^{1})$ と $f_{\sigma}(x^{1}) = 0$ とすれば元に戻る。

一般には $f_{\mu}$ , $f_{\sigma}$ は解析的には解けないからニューラルネットワークで近似する。
モデルが単純すぎる気がするけど、こういうことだと思う。

🤨🤔😑😨😱

このモデル、 $x^{2}$ も解析的に解けるか？

$x^{2}$ を解析的に解くことは、初期条件を $\delta$ じゃなくて正規分布にすることと変わらない。
初期条件が正規分布の場合、解けるんだろうか。

なるほど、

x^{0} \sim \mathcal{N} (\mu,\sigma^2)

の時、 $\sigma = 1$ だったら $f_{\mu}(x^{1}) = - \sqrt{1-\beta} \overline{x^{1}}$ と $f_{\sigma}(x^{1}) = 0$ がいい気がする。 $\sigma \neq 1$ だと何がいいのかはわからないなぁ。乱数は足せば足すほど分散が増えるから元の正規分布からは遠ざかる気はする。うーん。

🤨🤔😑😨😱

model probability, training：

Loss関数の評価の部分はわからないなぁ。
全体を積分するのは困難だから、式変形して下限を押し上げてるのはわかるけど、細かい数式の評価の部分は追えない。条件付き確率とKLダイバージェンスの計算に慣れてないと無理だなぁ。

🤨🤔😑😨😱

ロス関数は丸写しして学習できた。

左上が元の分布で、右上に向かって拡散させる。（フォワード軌道）
右下の分布を生成して、左下に向かって逆拡散させる。（リバース軌道）

動画。

https://youtu.be/LLbjjaaMhj0

🤨🤔😑😨😱

数式はこの記事が詳しい。

🤨🤔😑😨😱

Denoising Diffusion Probabilistic Models
Jonathan Ho, Ajay Jain, Pieter Abbeel
19 Jun 2020

https://arxiv.org/abs/2006.11239

拡散モデルを画像生成に使った最初の論文？
時期的にGANの学習が難しいことがわかってきたぐらいに出たのかなぁ。（StyleGANが3 Dec 2019なので）

🤨🤔😑😨😱

経験的にHo et al. (2020)は以下の係数を無視したロス関数を使うとdiffusion modelの学習がよりうまく行くことを発見しました。

出典：https://zenn.dev/nakky/articles/09fb1804001ff8#simplification

なるほど。そんなこと書いてあるのかこの論文
（学術論文って経験的には〇〇って書いていいんだ、、、）

🤨🤔😑😨😱

timestep embedding

hugging faceの実装

可視化する。

emb = get_timestep_embedding(torch.tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), 512)
print(emb.size())

plt.plot(emb.numpy().T)
plt.show()

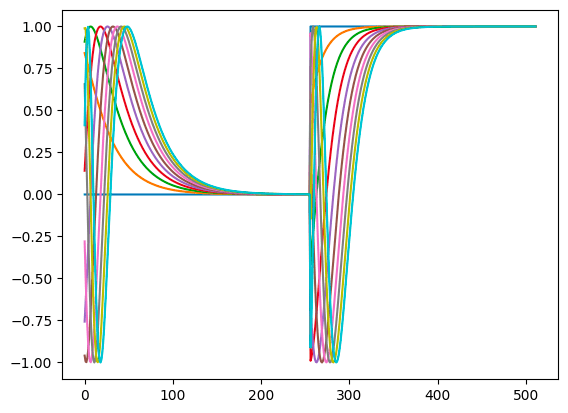
これでいいのか？

真ん中で不連続に変化するのは良いのか？
Positional embeddingとの違いは？

🤨🤔😑😨😱

この論文はtimestep = 1000なのか。実装してみたけど推論にすごい時間がかかる。。。

Attentionは使わないResNetブロックのみでUnet作って、CIFAR10をtimestep=1000ステップepoch = 10だけ回してみた。

timestep=1000だからepoch = 10だと学習すべき空間のほとんどを学習できていない気がするが、一応学習は進んでいる様子。

🤨🤔😑😨😱

timestep=50, epoch=100で学習回した。学習は進まなかった。。

timestep=50ではが画像に挿入された乱数を取り除けないのか。

それともbetaのスケジュールを論文の通り（beta = torch.linspace(1e-4, 0.02, timestep)）にしてるんだけど、これではいけないのか。

よく考えると拡散モデルって累積的に画像を乱雑にしていくから、timestep回だけ乱雑さを加えたら正規分布になっているようにbetaのスケジュールは調整しないといけない気がしてきた。
だから、timestep=1000の時のbetaのスケジュールとtimestep=50の時のbetaのスケジュールは異なる気がするなぁ。

🤨🤔😑😨😱

なるほど、timestep = 1000の時は、論文中のスケジュールで完全に拡散される状態になるっぽい

import torch

T = 1000
beta = torch.linspace(1e-4, 0.02, T)
alpha = 1 - beta
alpha_bar = alpha.cumprod(dim=0)
alpha_bar_t = alpha_bar[T - 1]
print(torch.sqrt(1 - alpha_bar_t), torch.sqrt(alpha_bar_t))

tensor(1.0000) tensor(0.0064)

同じスケジュールで、timestep = 50を計算すると、完全に拡散された状態にならないので学習が進まないのか。

import torch

T = 50
beta = torch.linspace(1e-4, 0.02, T)
alpha = 1 - beta
alpha_bar = alpha.cumprod(dim=0)
alpha_bar_t = alpha_bar[T - 1]
print(torch.sqrt(1 - alpha_bar_t), torch.sqrt(alpha_bar_t))

tensor(0.6301) tensor(0.7765)

なるほど、面白いね。

🤨🤔😑😨😱

この条件で学習させてみた。

timestep = 50
beta = torch.linspace(1e-4, 0.4, timestep)

さっきよりは進んだ。

やはりtimestep=1000であることは重要らしい。

🤨🤔😑😨😱

学習初期段階のモデルの出力値が気になっている。

DCGANの場合は最後にtanhしているので、-1 ~ 1であることが確定している。その一方でUNetベースの拡散モデルの場合は、最後でtanhをしないため学習初期段階は全く違う領域(数千とか数万とか)の値を出力している。モデルの初期値を調整して、初めから-1 ~ 1を出力させることは重要なんだろうか。

🤨🤔😑😨😱

生成される画像が初期値から決定できないのが気になっている。

DCGANの場合は、最初に入力する乱数が同じであれば、生成される画像も同じだったわけだけど、Diffusion modelの場合は逆拡散過程においても乱数を使うので、同じ乱数を入れたとしても生成される画像は異なると思う。なのでこういう動画は作れないかも。

🤨🤔😑😨😱

CIFAR10を
timestep = 1000
beta = torch.linspace(1e-4, 0.02, timestep)
epoch = 100
計算してみた。

モデルは、元論文のU-NetからAttentionレイヤーを除いたもの。32 x 32ぐらいならAttentionなくてもそれぽい画像は出てくる。一方でtimestepを減らすとそれっぽい画像は出てこなくなる。

なんか色が全体的に偏る。これはなぜ？学習してると色味が振動してるように見えるんだけど。私の作ったモデルの構造や初期値が悪いのか。

🤨🤔😑😨😱

Attentionを加えて学習させてみている。途中でロス関数が増えて全く見当違いの画像が出てくる。これはなぜだろう。過学習かな。拡散モデルはGANとは違ってこういうのは起こりにくいのかと思っているが。

Epoch 45, Loss: 0.0129
Epoch 46, Loss: 0.0269
Epoch 47, Loss: 1.0001
Epoch 48, Loss: 0.9980

`Epoch = 40`	`Epoch = 50`

🤨🤔😑😨😱

学習率落としたら普通に最後まで学習できた。

良いんじゃないでしょうか。

Self-Attentionを除いた場合とそこまで差が無いように見える。Self-Attentionいる？

🤨🤔😑😨😱

ELBO

🤨🤔😑😨😱

VAEのロス関数の不等式評価には名前がついてた。ELBOって言うらしい。
Diffusion Modelも同じ？評価方法を使ってる。

🤨🤔😑😨😱

わかりやすそうなレビュー論文と日本語の書籍もあるっぽい

https://arxiv.org/abs/2208.11970

🤨🤔😑😨😱

良さそうな記事（の日本語訳）

$\beta$ のスケジューリングの論文とか数式を使ってまとまってる。

🤨🤔😑😨😱

dlshougiのyamaokaさんの記事

🤨🤔😑😨😱

HuggingFaceのdiffusion modelsの解説ノートブック

日本語訳もある。

🤨🤔😑😨😱

拡散モデルの研究の分類

色んな論文をよく整理してくれている。順番に調べてけば歴史は理解できそう。

上記の記事の著者が、拡散モデルがなぜUnetひとつしか学習しないのか考えた記事

確かに2015年の最初のやつは50個のモデルを学習してる。2020年になってtimestep embeddingを加算することで一つのモデルを学習するようになった。不思議といえば不思議か。

二個目の記事の基本は小さいノイズを何度も与えるは結構重要そうな考察。

🤨🤔😑😨😱

2020年の論文について数式と図解がわかりやすい。3Dや動画への応用についてもまとまってる。

2020年の論文は画像にノイズを載せて、ノイズを当てるように学習させているんだということ数式使ってわかりやすく説明しようとしてる。
私はこのスライドを見てそれがクリアにわかった。

🤨🤔😑😨😱

もし生物情報科学専攻の学部生が "StableDiffusion" を理解しようとしたらシリーズ

この方は、数式ちゃんと追ってて素晴らしい。

🤨🤔😑😨😱

Stable Diffusionの論文

https://arxiv.org/abs/2112.10752

手元で学習できなくなると一気にやる気なくなるよなぁ

🤨🤔😑😨😱

非平衡統計力学入門：現代的な視点から

🤨🤔😑😨😱

リウヴィルの定理 (物理学)

エネルギー保存する環境の時間発展では、ある特定の状態が特別に選択されることはない。

TODO: 1次元調和振動子の例を計算する。

🤨🤔😑😨😱

ジャルジンスキー等式

何に使えるのかいまいちよくわからない。熱力学第二法則は導けるのはわかったけど。

🤨🤔😑😨😱

ゆらぎの定理

状態Aから状態Bに遷移する確率と状態Bから状態Aに遷移する確率に関係式が成り立つらしい。
これも何に使うのかいまいちわからない。

🤨🤔😑😨😱

詳細釣り合い条件

モンテカルロシミュレーションする際に出てくるやつ。

🤨🤔😑😨😱

シャノンエントロピー

https://ja.wikipedia.org/wiki/情報量

$\log(1/P)$ がびっくり度合いを数値化したもの。 $P = 10^-6$ で当たる宝くじがあった時、宝くじが当たった時のびっくり度合いは $\log(1/P)$ で数値化できる。逆に、宝くじが当たるという情報を事前に知っているということは、 $\log(1/P)$ の情報を事前に知っているということなので、 $\log(1/P)$ は情報量というらしい。（情報通信とかの文脈でこういう名前になるのだと思う。）

その上で、シャノンエントロピー（平均情報量）とは、確率分布全体でびっくり度合いを平均したもの。 $P = 10^-6$ の宝くじの場合は、ほとんどハズレなので、平均情報量が低い。逆に $P = 0.5$ のじゃんけんの場合は、どっちが当たるかわからないので平均情報量がが高い。

以下、物理

カノニカル分布において、シャノンエントロピーを計算すると、結果は物理のエントロピーと一致する。カノニカル分布の時だけ一致する。

🤨🤔😑😨😱

KL divergence　（相対エントロピー）

二つの確率分布の距離と解釈できる。必ずゼロ以上で距離がゼロなら二つの確率分布は等しいから。（ちなみに対称性がないので厳密な距離じゃない。）

動画中では、シャノンエントロピーより相対エントロピーの方が、物理的には本質的な量と言っていた。多分以下のようなことを言ってる。
「状態数が決まっている時、一様分布はその状態数の中で最大のシャノンエントロピーとなる確率分布である。その上で、一様分布とある確率分布の相対エントロピーを計算すると、それは情報エントロピーの差となる。そのため、情報エントロピーとは、一様分布との差を考える際の量である。」

以下、謎定理

任意の二つの確率分布を用意する。これらの確率分布を確率行列で変換して2つの確率分布を得る。この時、変換した後の確率分布の相対エントロピーは、元の相対エントロピーより必ず小さい。

確率行列を無限回作用させると、確率行列の固有ベクトルが与える確率分布に収束するはず。なので、一回かけるとお互いの距離が固有ベクトルに向かって縮むんだと思う。

よく考えたらこれって拡散モデルに関係あるかも。拡散モデルの前進過程って、マルコフ過程で遷移する先は初期状態に依存せずに、解析しやすい正規分布であるって話だし。

🤨🤔😑😨😱

ペロン＝フロベニウスの定理

確率行列の持つ、固有値1の固有ベクトルを議論できる定理らしい。機械学習で重要らしい。

🤨🤔😑😨😱

マルコフ連鎖　状態が離散で時間も離散

最も扱いが楽。金融の二項価格モデルや、将棋AIとかはこれ。
拡散モデルは、これの状態が連続バージョンを扱っている。

マルコフ再生過程　状態が離散で時間が連続

マルコフ再生過程でジャンプする時間が指数分布に従うとき、マルコフジャンプ過程という。この講義はマルコフジャンプ過程を扱っている。

拡散過程　時間も状態も連続。

ブラックショールズ方程式やブラウン運動はこれ。関数解析が必要で難しそう。

マルコフ過程は一個きちんと勉強すれば、他は大体類推でいける気がしている。この物理の講義を真面目に取り組んじゃって勉強しちゃうか。

🤨🤔😑😨😱

まとめ

拡散モデルとは

元の状態に（物理の意味で）拡散させていって乱雑にしていく。
この過程を学習データとして、逆方向を機械学習で近似する。
学習の際には、拡散過程の微小時間を考えるとき順軌跡と逆軌跡の確率過程が同じ関数の形をしていることや、ELBOなどの手法を使って、うまいこと式変形して学習できるようにする。
推論時には、十分に拡散された状態の正規分布からサンプルを取り出して、逆軌跡を辿って元の状態を復元する。
このモデルをUnetで学習したらうまいこと画像が生成できました。