🔖

レコメンドシステム—— FM（Factorization Machine）の理論

2023/09/27に公開

機械学習

 シリーズの目次レコメンドシステムのシリーズをここにまとめています。

https://zenn.dev/datasciencekun/articles/dc0f61c0ca7f8d
無料相談コース(未経験OK)
機械学習やレコメンド分野でお悩みの方
機械学習やレコメンド分野に携わりたい方（理論から実装まで）
ぜひ下記の無料コースへお申し込みください！

機械学習エンジニア、レコメンドエンジニアになるためのサポート

 FM（Factorization Machine）とは？Factorization Machine（FM）は、スパースな特徴量を持つ大規模データセットに対して高い予測精度を実現する革新的な機械学習モデルです。特に推薦システムの分野において、その効果的なアプローチが高く評価され、幅広く採用されています。

 レコメンデーションシステムの重要指標推薦システムの性能評価において、以下の2つの指標が特に重要視されています：
CTR（Click-through Rate：クリック率）
CVR（Conversion Rate：コンバージョン率）
これらの指標を精密に予測することは、以下の観点から重要です：
トラフィック価値の最大化
レコメンデーション精度の向上
ユーザー体験の改善

 予測手法の種類CTR/CVRの予測には、以下のような手法が一般的に用いられています：
特徴量エンジニアリング + ロジスティック回帰（LR）
GBDT（Gradient Boosting Decision Tree）+ LR
FM（Factorization Machine）
ディープラーニングベースのアプローチ
本記事では、FMモデルの基本原理と実装方法について、理論的な観点から詳しく解説していきます。

 FMの公式Factorization Machine（FM）は、2010年にKonstanz大学のSteffen Rendle氏（現Google）によって開発された、スパースデータにおける特徴量の組み合わせ問題を効率的に解決するアルゴリズムです。その概念を広告クリック予測の例を用いて説明します。この問題では、ユーザーと広告スペースの特徴を基に、広告クリックの可能性を予測します。
サンプルデータは以下の通りです：

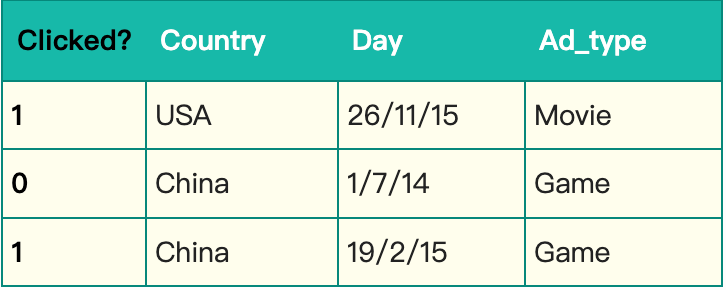
このデータでは：
Clicked：目的変数（ラベル）
Country、Day、Ad_type：説明変数（特徴量）

これらのカテゴリカル変数はOne-hotエンコーディングによって数値化する必要があります：

 データのスパース性についてOne-hotエンコーディング後のデータには、顕著なスパース性が見られます。例えば：
7次元の特徴空間において、各サンプルで実際に値を持つのは平均3次元のみ
これは特殊なケースではなく、実務では一般的な現象
実際のCTR/CVR予測では、以下のような特徴量でスパース性が発生します：
ユーザー属性（性別、職業、学歴など）
商品カテゴリー（約550種類のサブカテゴリー）
550次元の特徴ベクトルが生成
各サンプルで有効な値は1つのみ


 特徴空間の拡大One-hotエンコーディングによって特徴空間が急激に拡大する課題があります。例えば：
単一のカテゴリカル変数（商品カテゴリー）が550次元の数値特徴量に変換
結果として、処理すべき特徴空間が大幅に増大

 特徴量間の相関性データ分析から、特徴量の組み合わせが予測精度に重要な影響を与えることが判明しています：
地域・季節性の相関：
「USA」×「Thanksgiving」
「China」×「Chinese New Year」
商品・属性の相関：
化粧品×女性ユーザー
スポーツ用品×男性ユーザー
映画チケット×映画愛好家
これらの相関関係を適切にモデル化することが、予測精度向上の鍵となります。

 多項式モデルの基本構造多項式モデルは、特徴量の組み合わせを自然な形で表現できる直感的なモデルです。このモデルでは、2つの特徴量 x_i と x_j の相互作用を x_ix_j として表現します。これは、両方の特徴量が非ゼロの値を持つ場合にのみ意味を持つ組み合わせ特徴量となります。本稿では、2次の多項式モデルに焦点を当てて説明します。

 モデルの数式表現公式1：

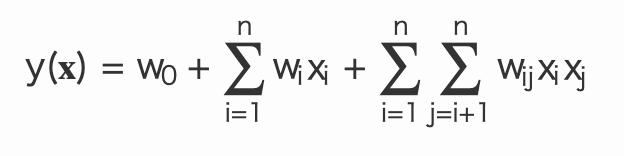
ここで：
n：特徴量の総数

X_i：i番目の特徴量の値

W_0、W_i、W_{ij}：モデルパラメータ

 モデルの課題
 パラメータ数の問題特徴量の組み合わせに関するパラメータ数は n(n-1)/2 個
各パラメータは独立して学習する必要がある

 スパースデータにおける学習の困難さパラメータ w_{ij} の学習には、x_i と x_j が同時に非ゼロとなるサンプルが十分に必要
データのスパース性により、この条件を満たすサンプルは極めて少数
学習サンプルの不足は以下の問題を引き起こす：
パラメータ W_{ij} の推定精度の低下
モデル全体の性能劣化

これらの課題は、実際のアプリケーションにおいて深刻な制約となる可能性があります。

 FMの解法導出
 行列分解による解決アプローチ二次項パラメータの学習問題に対して、行列分解（Matrix Factorization）は効果的な解決策を提供します。この手法は協調フィルタリングの考え方に基づいており、評価行列をユーザー行列とアイテム行列に分解することで、各要素の潜在的なベクトル表現を獲得します。
具体的な例として、以下の図では：


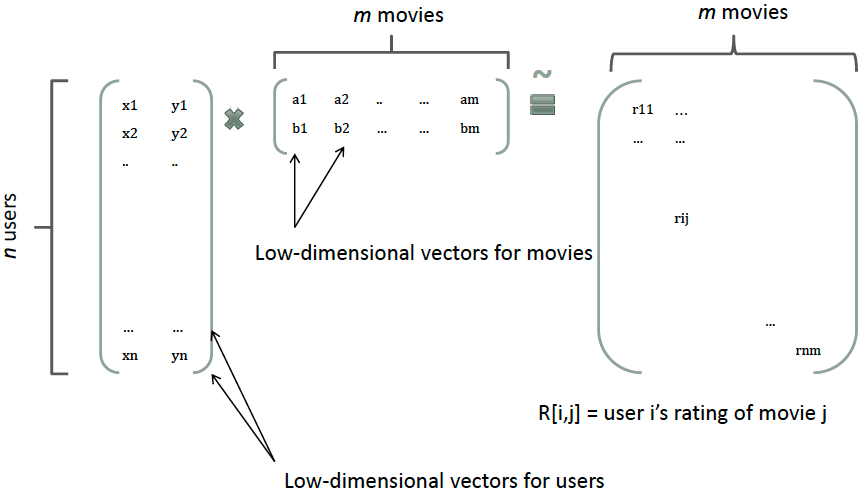
 モデルの数学的定式化すべての二次項パラメータ W_{ij} は対称行列 W として表現でき、W=V^TV という形で分解することができます。この分解において：
V の各列は特徴の潜在ベクトルを表現
すべてのパラメータは W_{ij}=⟨V_i,V_j⟩ として表現可能

これがFMモデルの核心的なアイデアとなります。
公式2：

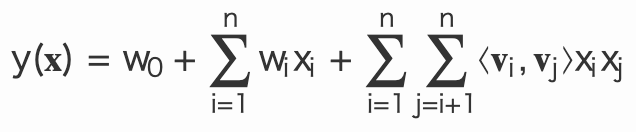
この式において：

V_i は特徴iの潜在ベクトル
⟨⋅,⋅⟩ はベクトルの内積
k は潜在次元数（k<<n）で、各特徴を表現するための因子数

 パラメータ学習の効率化この手法により：
パラメータ数が kn に大幅削減

x_hx_i と x_ix_j のパラメータ間に相互依存関係が生まれ
スパースデータでも安定した学習が可能に

 モデルの汎用性と最適化FMモデルは様々な問題に適用可能：
回帰問題：MSE損失関数を使用
分類問題：Hinge損失やCross-Entropy損失を使用
バイナリ分類：シグモイド関数による変換
計算効率の最適化：

公式3：


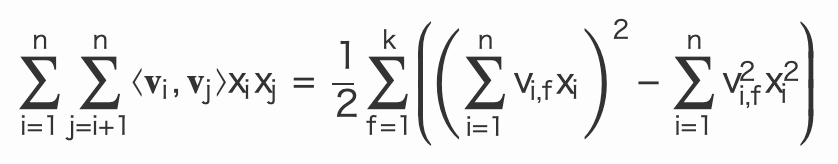
 確率的勾配降下法による効率的な学習SGDによるパラメータ更新：

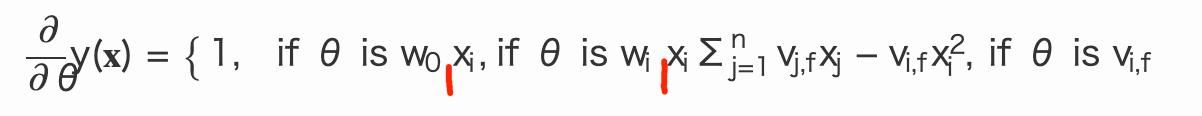
最適化のポイント：

V_{j,f} は潜在ベクトル V_j の第f成分

Σ^n_{j=1}V_{j,f}X_j の効率的な計算
全体の計算量をO(kn)に抑制
この実装により、FMは線形時間での学習と予測を実現する、極めて効率的なモデルとなっています。

 おわりに
 FMモデルの柔軟性と汎用性Factorization Machine（FM）は、その柔軟な設計思想により、以下のような様々な機械学習モデルの特性を包含することができます：
SVMの二次多項式カーネル
Matrix Factorization（MF）
SVD++モデル

 既存モデルとの比較
 SVMとの比較FMは以下の点でSVMの二次多項式カーネルを上回ります：
スパースデータへの適応力が高い
学習・予測の計算量が線形時間で済む
大規模データセットでの実用性が高い

 Matrix Factorizationとの比較FMはMFの拡張として以下の利点を持ちます：
特徴量の種類に制限がない
ユーザー特徴
アイテム特徴
その他任意の補助特徴（購買履歴の平均値など）

より豊富な特徴表現が可能
より柔軟なモデリングが可能
このような特性により、FMは実務上の推薦システムにおいて、より効果的かつ実用的なソリューションを提供することができます。