レコメンドシステム——行列分解(Matrix Factorization )

シリーズの目次

レコメンドシステムのシリーズをここにまとめています。
https://zenn.dev/datasciencekun/articles/dc0f61c0ca7f8d

無料相談コース(未経験OK)

• 機械学習やレコメンド分野でお悩みの方
• 機械学習やレコメンド分野に携わりたい方（理論から実装まで）

ぜひ下記の無料コースへお申し込みください！
機械学習エンジニア、レコメンドエンジニアになるためのサポート

以下は添付された文章の日本語をブラッシュアップしたものです。元のMarkdown構成は維持しています。

行列分解とは？

行列分解の紹介

パーソナライズされたレコメンデーションにおいて、マトリックス分解モデルを使用することは、従来のUserCFやItemCFといった隣接ベースの協調フィルタリング手法よりも優れています。そのため、マトリックス分解は現在、パーソナライズドレコメンデーションの研究分野において主流のモデルとなっています。

行列分解とは、直感的には元の大きな行列を2つの小さな行列の積として近似的に表現することです。実際のレコメンデーション計算では、分解された2つの小行列を使用します。具体的には、元の (m \times n) 行列を、2つの小行列 (m \times k) と (k \times n) に分解します。この (k) は「隠れ変数」または「潜在因子」と呼ばれる次元です。

マトリックス分解によるレコメンデーションアルゴリズムの中心的な仮定は、ユーザーやアイテムを潜在因子（隠れ変数）で表現し、それらの積が元の行列要素を近似するというものです。この仮定は、実際のインタラクションデータがユーザーとアイテムの共通特徴（例えば属性や好み）を反映し、それが隠れた変数に影響されると考えられるためです。

分解後の2つの小行列は、それぞれユーザーの潜在特徴とアイテムの潜在特徴を表します。また、行列要素の値は、ユーザーやアイテムがそれぞれの潜在因子にどれだけ一致しているかを示します。

映画を例にすると、映画には俳優、ジャンル、テーマ、時代などの隠れた要素があると考えられます。例えば、潜在因子の数 (k) を2とし、コメディとアクションのジャンルを表すとします。この場合、分解された2つの小行列は、それぞれの映画が2つのジャンルにどれほど適合しているか、また各ユーザーがそれらのジャンルをどれだけ好んでいるかを表します。

一般的に、潜在因子の数 (k) は、ユーザー数やアイテム数よりも大幅に少なく設定されます。大行列を2つの小行列に分解することは、ユーザーとアイテムを (k) 次元の潜在空間上にマッピングすることを意味します。このマッピングにより、ユーザーとアイテム間の距離が近いほどユーザーがそのアイテムを好む可能性が高いと解釈できます。

行列分解の理論

機械学習の観点から見ると、映画のスコア予測において、元の大行列にはスコアが記録されていない箇所が多く含まれることが分かります。つまり、部分的にしかスコアが存在しない行列を、2つの小行列の積で補完します。

このとき、最適な2つの小行列を構築することが課題となります。元の行列で既にスコアがある位置（実際値）と、分解後の小行列の積で得られる位置（予測値）の誤差を最小化するように学習を進めます。この誤差は一般に平均二乗誤差（MSE）として表され、これがモデルの損失関数となります。

このような潜在因子モデルは、「潜在因子モデル（Latent Factor Model, LFM）」と呼ばれます。LFMはもともとテキスト解析の分野で考案されましたが、現在ではマトリックス分解を代表的な応用として、レコメンデーションシステムにも広く用いられています。

行列分解の解析

特異値分解（SVD: Singular Value Decomposition）

マトリックス分解の代表例として挙げられるのが特異値分解（SVD）です。理論的には、SVDを直接的にレコメンデーションに応用することも可能です。ユーザー-アイテムのスコア行列 (A) をSVDで分解し、主要な特異値を選択することで次元を削減します。

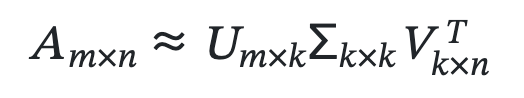
ここで、(k) は行列 (A) の主要な特異値の数を示し、通常、ユーザーやアイテムの数よりも少ない値が選択されます。この方法により、ユーザー (i) に対するアイテム (j) の予測スコア (a_{ij}) を計算することができます。具体的には、(u_i^T)、(\Sigma)、(v_j) を掛け合わせます。

このアプローチでは、スコアが未定義の箇所をすべて予測し、高スコアのアイテムをユーザーに推薦することが可能です。

特異値分解の課題

ただし、SVDをそのままレコメンデーションシステムに適用する際には、いくつかの問題があります：

1. 行列の密度
   SVDは行列が密であることを前提としていますが、実際のスコア行列は疎であり、欠損値が多いため、そのままでは使用できません。これを解決するためには、欠損部分をグローバル平均やユーザー・アイテム平均で埋める必要があります。しかし、こうしたデータ補完は、データ量の増加や歪みを引き起こしやすいです。

2. 計算コスト
   (m \times n) の行列を分解する計算コストは (O(n^2 \cdot m + n \cdot m^2))、あるいは (O(n^3)) に達します。データ規模が数百万に及ぶレコメンデーションシステムでは、計算負荷が非常に大きくなります。

これらの理由から、SVDを直接適用するのではなく、他のアプローチが必要です。

勾配降下法（SGD: Stochastic Gradient Descent）

次に、勾配降下法（SGD）を用いた行列分解の手法について、具体例を挙げながら説明します。

以下は、スコア行列 (R(5,4)) の例です（「-」はユーザーが採点していないことを示します）。

ここで、行列 (R(n,m)) は (n) 行 (m) 列の構造を持ち、(n) はユーザー数、(m) はアイテム数を表します。この行列に基づいて、未採点部分のスコアを予測します。

行列分解では、元の行列 (R_{n \times m}) を、2つの小行列 (P_{n \times k})（ユーザーと特徴の関係行列）と (Q_{k \times m})（アイテムと特徴の関係行列）に分解します。

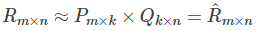
分解の詳細

• 行列 (P(n, k)) は、ユーザーと (k) 個の潜在特徴の関係を表します。
• 行列 (Q(m, k)) は、アイテムと (k) 個の潜在特徴の関係を表します。

正則化損失関数

オーバーフィットを防ぐため、損失関数に正則化項を追加します。損失関数は以下のように定義されます：

1. 損失関数
   未知のスコアを近似するための基礎式：
   

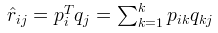
2. 正則化項の追加
   モデルの一般化能力を高めるために (L_2) 正則化を導入：
   

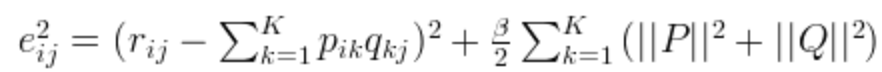
   これにより、以下のような損失関数が得られます：
   

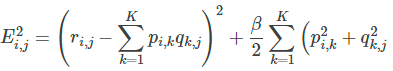
3. 勾配降下法によるパラメータ更新
   勾配降下法を用いて、行列 (P) および (Q) の成分を更新します。損失関数の負の勾配を計算し、変数を反復的に更新します：
   
   

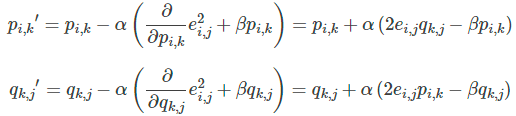
4. 収束判定
   二乗誤差の合計が設定した閾値以下になるまで繰り返します。

最終結果

このプロセスを通じて、行列 (P) と (Q) を取得し、これらを用いて商品 (j) に対するユーザー (i) のスコアを予測します。

まとめ

メリット

1. 効率的な計算
   高次元のスコア行列を低次元に分解することで、メモリ消費を削減し、効率的なオフライン学習が可能です。学習後のモデルはリアルタイムの予測にも適用できます。

2. 高い精度
   従来の協調フィルタリングやコンテンツベースフィルタリングに比べて、より高い予測精度を実現します。

3. 拡張性
   ユーザーやアイテムの特徴ベクトルに追加情報を柔軟に組み込むことができます。

デメリット

1. モデルの学習に時間がかかる。
2. 推薦結果を説明するのが難しい。