やさしいYield Space
今日の固定金利DeFiの基本となっているDEX
Yield Spaceの性質を雰囲気で伝えます。
なぜYield Spaceがゼロクーポン債の取引に適しているか
ゼロクーポン債とは何か
Yield Spaceの性質
Yield Spaceの目的
Yield Spaceは、トークン化されたゼロクーポン債のトークンを取引するためのAMMです。ゼロクーポン債の金利(インプライドフォワードレート)を発見をするという役割があります。
そもそもゼロクーポン債とはなんでしょうか?
ゼロクーポン債とは
ゼロクーポン債(割引債)とは、債券のクーポン(表面利息)が無い代わりに、発行価額を割引する形態をした債券のことです。債券は満期を迎えると、額面100に対して100で償還されます。普段耳にする債券は四半期や一年毎など一定期間毎に金利が支払われますが、ゼロクーポン債は利子の支払いがない債券です。利子の支払いがない分だけ割引かれた価格で取引されます。発行価額と額面金額の差がクーポンを補完する役割を持つため、相応な償還差益を得ることが可能です。
例えば、満期がちょうど一年後の日付である、額面 100 DAIのゼロクーポン債を市場から90 DAIの価格で買ったとします。そのまま保有して、満期を迎えると額面 1 00DAIで償還することができます。つまり、購入(割引されている)価格と額面の差が、満期で受け取る利子相当額になります。よって、購入した時点で一年後の10DAIの利益(11.1%の最終年利回り(単利))を確定することができます。
インプライドフォワードレートはゼロクーポン債を満期日まで保有することで得られるリターンを年率で表したものです。
Yield protocol, Element finance, Pendle, Sense financeなどの固定金利DeFiは、このような「イールド・ストリッピング」と言われるゼロクーポン債を利用したアプローチをとっています。
ゼロクーポン債は額面価格より割引された価格で取引されます。では、ある時刻にどのくらいの価値で評価されるべきなのでしょうか。少し深掘りしてみましょう。早く次に進みたい方はこの部分を飛ばしてもいいです。
満期直後にキャッシュフローを受け取ることができるため、割引現在価値のモデルを適用します。

ここで、
PV = Present value: 現在価値 = ゼロクーポン債の市場価格 [原資産建て]
FV = Future value: 将来価値 =ゼロクーポン債の額面 [原資産建て]
r = 割引率(年率)
t = 満期までの年数 (分数にもなりうる)
原資産: DAIやETH, USDC
です。
FVを1, PVを p とおいて、式を整理すると

となります。
例えば、市場価格 0.972 DAIの1年後に満期を迎えるゼロクーポン債の割引率は 2.88%です。この数値が市場参加者が考えている金利です。
r = (1 / 0.972)^1 -1 = 2.88 %
上記の例では、ゼロクーポン債を市場から購入しています。DeFiの世界では「市場」とは主に、Uniswapに代表されるようなDEXです。
では、なぜUniswapのようなAMMではなく、Yield Spaceが必要なのでしょうか。以降は、プールのアセットは原資産とゼロクーポン債トークンのペアとします。
なぜYield Spaceが必要か
先ほど、ゼロクーポン債は満期後に額面(1 DAI)で償還できると言いました。理想的には満期日が近づくにつれて割引が徐々に減っていき、満期直前には額面と同じ価値に収束します。言い換えると、プール内のゼロクーポン債トークンの比率が満期日が近づくにつれて、減少していきます。
このように、時間の経過とともにゼロクーポン債トークンの価値は予測可能的に変わるが、時間の因子を含まないx * y = 一定, x * y + α (x + y) = 一定
のような従来の不変条件では必然的に変動損失を避けることができません。 そこで、Yield Spaceは新しい不変条件である「constant power sum formula」(冪乗和一定)を導入しました。
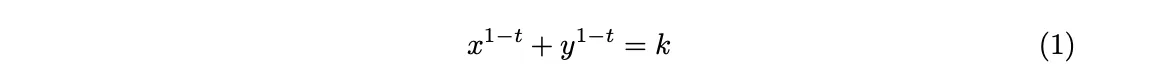
ここでx, yはそれぞれプール内の原資産の数量, プール内のゼロクーポン債トークン(fyDAI)の数量, tはゼロクーポン債トークンの残存時間です。(t = 0の時が満期です) t の単位は0≤ t <1になるように正規化されているとします。
プール内のアセット量を変数として、不変条件(1)を満たす曲線の軌跡を描くと、次の図のようになります。時間に応じて曲線の形状が大きく変化します。
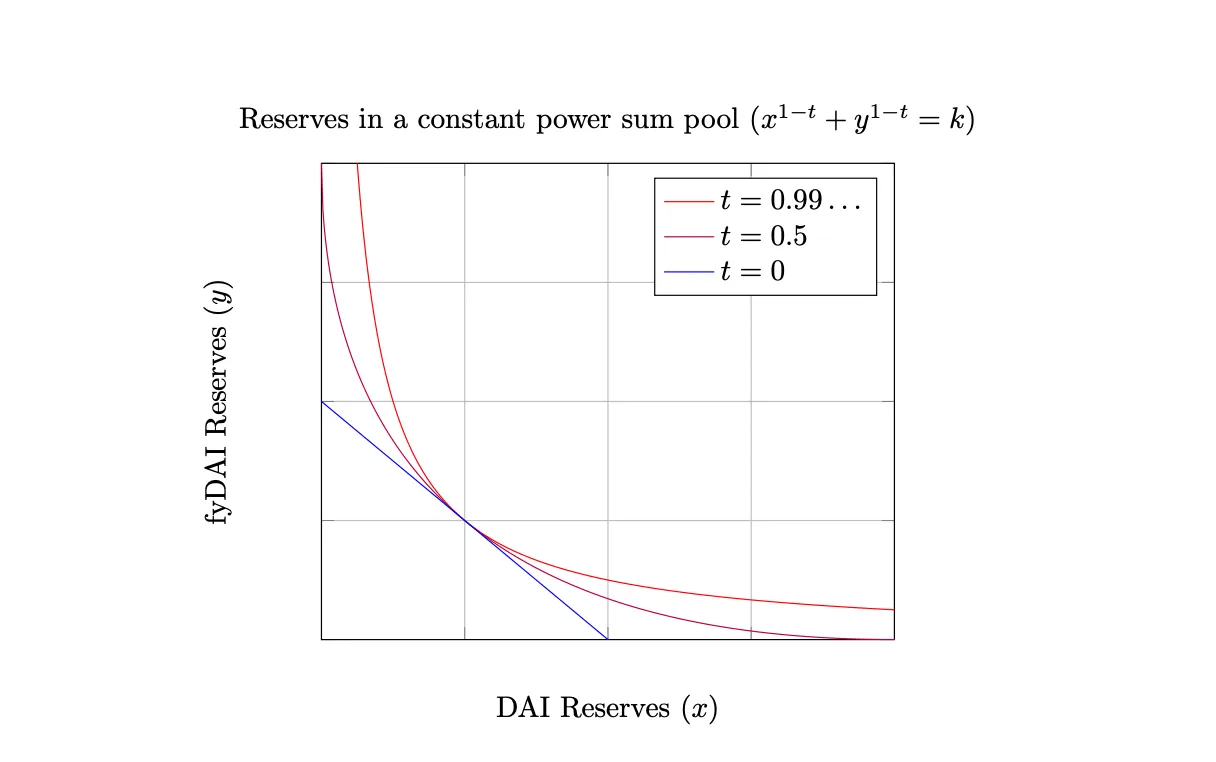
曲線上の任意の点における、ゼロクーポン債トークン(fyDAI)の原資産(DAI)建ての価格(相対価格)は、プールに少量(dx)が入ってきたときに出ていく量(-dy)から考えることができるので、接線の傾きの負の逆数(-dx/dy)です。
補足: プールに入ってくる方向を正としているので、-dyが出ていく量です。
満期(t = 0のとき)
曲線は図の青線のように、mStable(おそらく)のようなx + y = 一定の不変条件になります。
曲線上のどの点でも接線の傾きは1であり、1fyDAIは1 DAIと交換できます。満期後のゼロクーポン債は額面と1対1で償還できるため、理にかなっています。
プール初期化直後(t → 1 極限のとき)
曲線は図の赤線のように、Uniswapのようなxy = 一定の不変条件に近似できます。満期の時の曲線と比べると、価格発見(金利発見)機能が優れています。プール初期化直後、トレーダー、アービトラージャーなどは尤もらしい金利(割引率)を見込んで、均衡するまで活発に売買を行うと期待されるため、この曲線は理にかなっています。
時間が経過する(tが1から0になる)につれて
曲線は図の赤線から青線に変化していきます。時間の経過に合わせて曲線が変化することで、変動損失を軽減します。ゼロクーポン債の金利は式(a)に基づいて市場で発見されます。
このシミュレーターでインタラクティブに曲線で遊べます。
このスプレッドシートで売買とプールの状態を再現できるようにしました。
補足: t → 1 極限で不変条件(1)がxy = 一定になることの証明
Yield Space White paperのAppendix Dに分かりやすく書かれているので省略しますが、簡単にいうと以下の式をy(x,t)の関数としてtの極限を求めます。

最後に、インプライドフォワードレートと価格がどのように表されるかを確認しましょう。
やや天下り的ですが、Yield Spaceの不変条件からゼロクーポン債トークンの価格は、
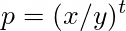
と導出できます。
よって、インプライドフォワードレートは、式(a)より

となります。プール内のアセットの数量が変化しないなら、インプライドフォワードレートは変わらないという重要な性質が分かります。
Uniswapのような時間に依存しない不変条件とYield Spaceの不変条件を比較してみましょう。
Uniswapのような不変条件
プール内のアセットの数量が変化しないなら、価格は変わらない。
Yield Spaceの不変条件
プール内のアセットの数量が変化しなくても、時間に依存して価格は変わる。
プール内のアセットの数量が変化しないなら、インプライドフォワードレートは変わらない。
UniswapのようなAMMではトークンの価格をプール内のアセット数量で表現します。一方でYield Spaceではインプライドフォワードレートをプール内のアセット数量で表現します。前者が「Price Space」と言われ、後者が「Yield Space」と名付けられた所以です。
まとめ
Yield Spaceの基本を説明しました。トークン化されたゼロクーポン債を取引するためのAMMとインプライドフォワードレートのオラクルとしての役割があります。
Yield Spaceは不変条件に時間の変数を含む。時間が経つにつれて、x*y = 一定の式から x + y = 一定の式へ動的に徐々に変化する。これによって、流動性提供者の変動損失を軽減する。
インプライドフォワードレートをプール内のアセット数量で表す。
Discussion