📐

TypstのCeTZパッケージで幾何学図形を描く：正方形と点の距離問題

2025/12/05に公開3件

はじめに

X（旧Twitter）で@HirokazuOHSAWAさんから面白い図形の問題が投稿されました：

この記事では、この問題をTypstとCeTZパッケージを使って可視化する方法を詳しく解説します。特にCeTZパッケージのコードについて丁寧に説明していきます。

問題と解答

まず問題を整理しましょう。

問題: 正方形ABCDの内部に点Pをとると、AP=5, BP=3, CP=7となった。この正方形の面積を求めよ。

解答: この問題の答えは 58 です（ $7^2 + 3^2 = 49 + 9 = 58$ ）。

点Pの位置は特定の条件下でのみ存在し、その場合の正方形の一辺の長さは $\sqrt{58}$ となります。

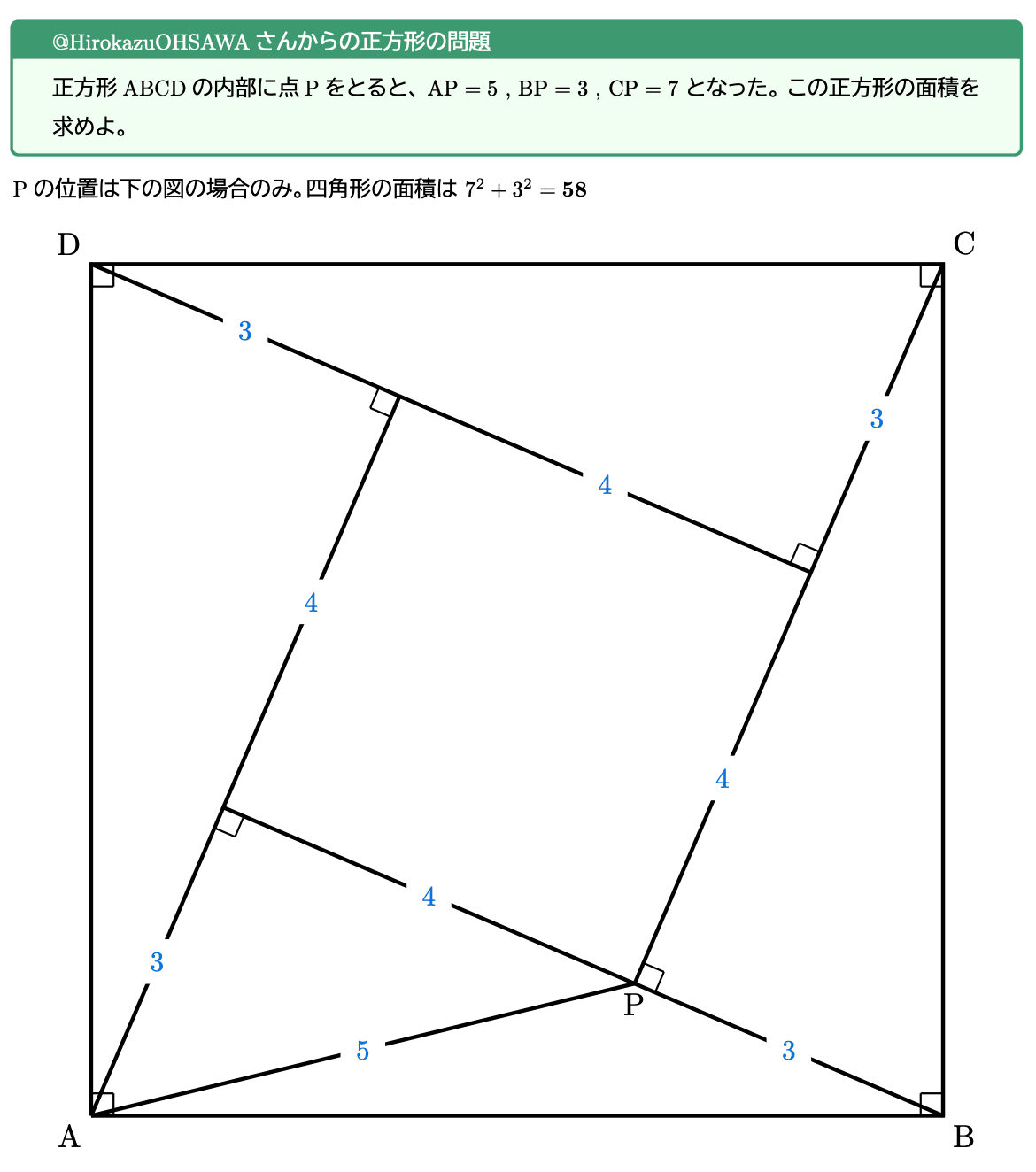
以下がCeTZで作成した図です：

CeTZで作成した幾何学図形

CeTZパッケージとは

CeTZは、Typstで図形を描画するための強力なパッケージです。座標系を使って点を配置し、線や図形を描くことができます。

まず、CeTZパッケージをインポートします：

#import "@preview/cetz:0.4.2"

座標の設定

この問題の図を描くために、まず座標系を設定します。正方形の一辺の長さは $\sqrt{58}$ なので、以下のように頂点を定義します：

let A = (0, 0)
let B = (calc.sqrt(58), 0)
let C = (calc.sqrt(58), calc.sqrt(58))
let D = (0, calc.sqrt(58))

点Pとその関連する点Q, R, Sの座標は、幾何学的な計算から導かれます：

let P = (calc.sqrt(58)-21/calc.sqrt(58), calc.sqrt(58)-49/calc.sqrt(58))
let Q = (49/calc.sqrt(58), calc.sqrt(58)-21/calc.sqrt(58))
let R = (21/calc.sqrt(58), 49/calc.sqrt(58))
let S = (calc.sqrt(58)-49/calc.sqrt(58), 21/calc.sqrt(58))

これらの座標は、点Pを中心とした正方形PQRSを形成し、各辺の長さが4となるように配置されています。

CeTZ描画の基本構造

CeTZで図形を描くには、cetz.canvas()関数を使用します：

#cetz.canvas(length: 2.0cm, {
  import cetz.draw: *
  // ここに描画コードを記述
})

length: 2.0cmは、座標系の単位長さを指定しています。つまり、座標1が実際には2cmとして描画されます。

正方形と線の描画

正方形の外枠

正方形ABCDを描画します：

line(A, B, C, D, A, stroke: (paint: black, thickness: 2pt))

この1行で、A→B→C→D→Aと頂点を結んで正方形を描画します。strokeパラメータで線の色と太さを指定します。

内部の線

点Pと各頂点を結ぶ線を描画します：

line(C, P, stroke: (paint: black, thickness: 2pt))
line(D, Q, stroke: (paint: black, thickness: 2pt))
line(A, R, stroke: (paint: black, thickness: 2pt))
line(B, S, stroke: (paint: black, thickness: 2pt))
line(A, P, stroke: (paint: black, thickness: 2pt))  // AP（問題で与えられた距離）

直角記号の描画

幾何学の図では、直角を示す記号が重要です。CeTZでは小さな正方形を描いて直角を表現します。

正方形の頂点の直角記号

例えば、頂点Aの直角記号は次のように描画します：

let size = 0.2  // 直角記号のサイズ
line((size, 0), (size, size), stroke: black)
line((0, size), (size, size), stroke: black)

これは、点(size, 0)から(size, size)へ垂直線を引き、点(0, size)から(size, size)へ水平線を引くことで、小さな正方形の2辺を描いています。

任意の角度での直角記号

点P, Q, R, Sでの直角記号は、辺の方向に沿って描く必要があります。そのため、ベクトルを正規化する関数を定義します：

let normalize = (vec) => {
  let len = calc.sqrt(vec.at(0) * vec.at(0) + vec.at(1) * vec.at(1))
  ((vec.at(0) / len, vec.at(1) / len))
}

この関数は、ベクトルの長さを1にします（単位ベクトル化）。

例えば、点Pでの直角記号は、辺SPとPQの方向に沿って描きます：

let v_sp = (px - sx, py - sy)  // ベクトルSP
let v_pq = (qx - px, qy - py)  // ベクトルPQ
let u_sp = normalize(v_sp)     // 正規化
let u_pq = normalize(v_pq)     // 正規化

// 直角記号の2辺を描画
line((px + u_sp.at(0) * psize, py + u_sp.at(1) * psize),
     (px + u_sp.at(0) * psize + u_pq.at(0) * psize, py + u_sp.at(1) * psize + u_pq.at(1) * psize),
     stroke: black)
line((px + u_pq.at(0) * psize, py + u_pq.at(1) * psize),
     (px + u_sp.at(0) * psize + u_pq.at(0) * psize, py + u_sp.at(1) * psize + u_pq.at(1) * psize),
     stroke: black)

これは以下のステップで直角記号を描いています：

点Pから2つの方向（SPとPQ）へ、単位ベクトルをpsize倍した距離だけ進む
それぞれの端点から、もう一方の方向へ同じ距離進む
小さな正方形の2辺を描画

テキストラベルの配置

距離の表示

辺の中点に距離を表示します。まず中点の座標を計算します：

let mid_pq_x = (px + qx) / 2
let mid_pq_y = (py + qy) / 2

次に、テキストの背景を白い矩形で描き、その上にテキストを配置します：

rect((mid_pq_x - 0.6, mid_pq_y - 0.2), (mid_pq_x + 0.6, mid_pq_y + 0.2),
     fill: white, stroke: none)
content((mid_pq_x, mid_pq_y), text(fill: blue, size: 14pt, [4]))

rect()で白い矩形を描き、content()でテキストを配置します。stroke: noneにより、矩形の枠線は描画されません。

頂点ラベル

頂点にA, B, C, Dのラベルを配置します：

content(A, anchor: "north-east", padding: 5pt, text(fill: black, size: 16pt, [A]))
content(B, anchor: "north-west", padding: 5pt, text(fill: black, size: 16pt, [B]))
content(C, anchor: "south-west", padding: 5pt, text(fill: black, size: 16pt, [C]))
content(D, anchor: "south-east", padding: 5pt, text(fill: black, size: 16pt, [D]))
content(P, anchor: "north", padding: 5pt, text(fill: black, size: 16pt, [P]))

anchorパラメータは、テキストの配置位置を指定します：

"north-east": テキストの右上を基準点に配置（Aは左下に表示される）
"north-west": テキストの左上を基準点に配置（Bは右下に表示される）
"south-west": テキストの左下を基準点に配置（Cは右上に表示される）
"south-east": テキストの右下を基準点に配置（Dは左上に表示される）

図全体のコード

最後に、完全なコードを示します：

#set page(
paper: "a4",
height: 297mm,
width: 210mm,
margin: (x: 1.5cm, y: 1.5cm),
)

#set par(
  justify: true,
  leading: 1em,
)

#set text(
  font: ("New Computer Modern","BIZ UDPMincho")
)

#show regex("[\p{scx:Han}\p{scx:Hira}\p{scx:Kana}]"): set text(font: "BIZ UDPGothic")
#set text(lang: "ja")

#set enum(numbering: "(1)",)

#import "@preview/colorful-boxes:1.4.2": *

#let my_block(back_color, frame_color, title_color, content_color, title, content) = {
  block(width:auto,radius: 4pt, stroke: back_color + 3pt)[
    #block(width: 100%,fill: back_color, inset: (x: 20pt, y: 5pt), below: 0pt)[#text(title_color,font: ("New Computer Modern","BIZ UDPMincho"))[#title]]
   #block(radius: (
    bottom: 3pt,
  ),width: 100%, fill: frame_color, inset: (x: 20pt, y: 10pt))[#text(content_color)[#content]]
  ]
}

#my_block(olive,rgb(95%, 100%, 95%) , white, black, [\@HirokazuOHSAWAさんからの正方形の問題], [正方形ABCDの内部に点Pをとると、
 $"AP" =5$ , $"BP" =3$ , $"CP" =7$ となった。
この正方形の面積を求めよ。

  ])

Pの位置は下の図の場合のみ。四角形の面積は $ 7^2 + 3^2 = bold(58)$

#import "@preview/cetz:0.4.2"
#figure(
cetz.canvas(length:2.0cm,{
  import cetz.draw: *

  let A = (0, 0)
  let B = (calc.sqrt(58), 0)
  let C = (calc.sqrt(58), calc.sqrt(58))
  let D = (0, calc.sqrt(58))
  let P = (calc.sqrt(58)-21/calc.sqrt(58), calc.sqrt(58)-49/calc.sqrt(58))
  let Q = (49/calc.sqrt(58), calc.sqrt(58)-21/calc.sqrt(58))
  let R = (21/calc.sqrt(58), 49/calc.sqrt(58))
  let S = (calc.sqrt(58)-49/calc.sqrt(58), 21/calc.sqrt(58))

  let size = 0.2
  let psize = 0.2

  // ベクトルを正規化する関数
  let normalize = (vec) => {
    let len = calc.sqrt(vec.at(0) * vec.at(0) + vec.at(1) * vec.at(1))
    ((vec.at(0) / len, vec.at(1) / len))
  }

  // 矩形ABCD
  line(A, B, C, D, A, stroke: (paint: black, thickness: 2pt))

  line(C, P, stroke: (paint: black, thickness: 2pt))
  line(D, Q, stroke: (paint: black, thickness: 2pt))
  line(A, R, stroke: (paint: black, thickness: 2pt))
  line(B, S, stroke: (paint: black, thickness: 2pt))

  // AP を結ぶ線
  line(A, P, stroke: (paint: black, thickness: 2pt))

  // A の直角記号
  line((size, 0), (size, size), stroke: black)
  line((0, size), (size, size), stroke: black)

  // B の直角記号
  line((calc.sqrt(58) - size, 0), (calc.sqrt(58) - size, size), stroke: black)
  line((calc.sqrt(58), size), (calc.sqrt(58) - size, size), stroke: black)

  // C の直角記号
  line((calc.sqrt(58) - size, calc.sqrt(58)), (calc.sqrt(58) - size, calc.sqrt(58) - size), stroke: black)
  line((calc.sqrt(58), calc.sqrt(58) - size), (calc.sqrt(58) - size, calc.sqrt(58) - size), stroke: black)

  // D の直角記号
  line((size, calc.sqrt(58)), (size, calc.sqrt(58) - size), stroke: black)
  line((0, calc.sqrt(58) - size), (size, calc.sqrt(58) - size), stroke: black)

  let px = P.at(0)
  let py = P.at(1)
  let qx = Q.at(0)
  let qy = Q.at(1)
  let rx = R.at(0)
  let ry = R.at(1)
  let sx = S.at(0)
  let sy = S.at(1)

  // P の直角記号（SP と PQ に沿って）
  let v_sp = (px - sx, py - sy)
  let v_pq = (qx - px, qy - py)
  let u_sp = normalize(v_sp)
  let u_pq = normalize(v_pq)

  line((px + u_sp.at(0) * psize, py + u_sp.at(1) * psize),
       (px + u_sp.at(0) * psize + u_pq.at(0) * psize, py + u_sp.at(1) * psize + u_pq.at(1) * psize), stroke: black)
  line((px + u_pq.at(0) * psize, py + u_pq.at(1) * psize),
       (px + u_sp.at(0) * psize + u_pq.at(0) * psize, py + u_sp.at(1) * psize + u_pq.at(1) * psize), stroke: black)

  // Q の直角記号（PQ と QR に沿って）
  let v_pq_q = (qx - px, qy - py)
  let v_qr = (rx - qx, ry - qy)
  let u_pq_q = normalize(v_pq_q)
  let u_qr = normalize(v_qr)

  line((qx + u_pq_q.at(0) * psize, qy + u_pq_q.at(1) * psize),
       (qx + u_pq_q.at(0) * psize + u_qr.at(0) * psize, qy + u_pq_q.at(1) * psize + u_qr.at(1) * psize), stroke: black)
  line((qx + u_qr.at(0) * psize, qy + u_qr.at(1) * psize),
       (qx + u_pq_q.at(0) * psize + u_qr.at(0) * psize, qy + u_pq_q.at(1) * psize + u_qr.at(1) * psize), stroke: black)

  // R の直角記号（QR と RS に沿って）
  let v_qr_r = (rx - qx, ry - qy)
  let v_rs = (sx - rx, sy - ry)
  let u_qr_r = normalize(v_qr_r)
  let u_rs = normalize(v_rs)

  line((rx + u_qr_r.at(0) * psize, ry + u_qr_r.at(1) * psize),
       (rx + u_qr_r.at(0) * psize + u_rs.at(0) * psize, ry + u_qr_r.at(1) * psize + u_rs.at(1) * psize), stroke: black)
  line((rx + u_rs.at(0) * psize, ry + u_rs.at(1) * psize),
       (rx + u_qr_r.at(0) * psize + u_rs.at(0) * psize, ry + u_qr_r.at(1) * psize + u_rs.at(1) * psize), stroke: black)

  // S の直角記号（RS と SP に沿って）
  let v_rs_s = (sx - rx, sy - ry)
  let v_sp_s = (px - sx, py - sy)
  let u_rs_s = normalize(v_rs_s)
  let u_sp_s = normalize(v_sp_s)

  line((sx + u_rs_s.at(0) * psize, sy + u_rs_s.at(1) * psize),
       (sx + u_rs_s.at(0) * psize + u_sp_s.at(0) * psize, sy + u_rs_s.at(1) * psize + u_sp_s.at(1) * psize), stroke: black)
  line((sx + u_sp_s.at(0) * psize, sy + u_sp_s.at(1) * psize),
       (sx + u_rs_s.at(0) * psize + u_sp_s.at(0) * psize, sy + u_rs_s.at(1) * psize + u_sp_s.at(1) * psize), stroke: black)

  // PQの中点に「4」を表示（白い背景付き）
  let mid_pq_x = (px + qx) / 2
  let mid_pq_y = (py + qy) / 2
  rect((mid_pq_x - 0.6, mid_pq_y - 0.2), (mid_pq_x + 0.6, mid_pq_y + 0.2),
       fill: white, stroke: none)
  content((mid_pq_x, mid_pq_y), text(fill: blue, size: 14pt, [4]))

  // QRの中点に「4」を表示
  let mid_qr_x = (qx + rx) / 2
  let mid_qr_y = (qy + ry) / 2
  rect((mid_qr_x - 0.2, mid_qr_y - 0.2), (mid_qr_x + 0.2, mid_qr_y + 0.2),
       fill: white, stroke: none)
  content((mid_qr_x, mid_qr_y), text(fill: blue, size: 14pt, [4]))

  // RSの中点に「4」を表示
  let mid_rs_x = (rx + sx) / 2
  let mid_rs_y = (ry + sy) / 2
  rect((mid_rs_x - 0.6, mid_rs_y - 0.2), (mid_rs_x + 0.6, mid_rs_y + 0.2),
       fill: white, stroke: none)
  content((mid_rs_x, mid_rs_y), text(fill: blue, size: 14pt, [4]))

  // SPの中点に「4」を表示
  let mid_sp_x = (sx + px) / 2
  let mid_sp_y = (sy + py) / 2
  rect((mid_sp_x - 0.2, mid_sp_y - 0.2), (mid_sp_x + 0.2, mid_sp_y + 0.2),
       fill: white, stroke: none)
  content((mid_sp_x, mid_sp_y), text(fill: blue, size: 14pt, [4]))

  // ASの中点に「3」を表示
  let mid_as_x = (0 + sx) / 2
  let mid_as_y = (0 + sy) / 2
  rect((mid_as_x - 0.3, mid_as_y - 0.2), (mid_as_x + 0.6, mid_as_y + 0.2),
       fill: white, stroke: none)
  content((mid_as_x, mid_as_y), text(fill: blue, size: 14pt, [3]))

  // BPの中点に「3」を表示
  let mid_bp_x = (calc.sqrt(58) + px) / 2
  let mid_bp_y = (0 + py) / 2
  rect((mid_bp_x - 0.2, mid_bp_y - 0.2), (mid_bp_x + 0.2, mid_bp_y + 0.2),
       fill: white, stroke: none)
  content((mid_bp_x, mid_bp_y), text(fill: blue, size: 14pt, [3]))

  // CQの中点に「3」を表示
  let mid_cq_x = (calc.sqrt(58) + qx) / 2
  let mid_cq_y = (calc.sqrt(58) + qy) / 2
  rect((mid_cq_x - 0.6, mid_cq_y - 0.2), (mid_cq_x + 0.3, mid_cq_y + 0.2),
       fill: white, stroke: none)
  content((mid_cq_x, mid_cq_y), text(fill: blue, size: 14pt, [3]))

  // DRの中点に「3」を表示
  let mid_dr_x = (0 + rx) / 2
  let mid_dr_y = (calc.sqrt(58) + ry) / 2
  rect((mid_dr_x - 0.2, mid_dr_y - 0.2), (mid_dr_x + 0.2, mid_dr_y + 0.2),
       fill: white, stroke: none)
  content((mid_dr_x, mid_dr_y), text(fill: blue, size: 14pt, [3]))

  // APの中点に「5」を表示
  let mid_ap_x = (0 + px) / 2
  let mid_ap_y = (0 + py) / 2
  rect((mid_ap_x - 0.2, mid_ap_y - 0.2), (mid_ap_x + 0.2, mid_ap_y + 0.2),
       fill: white, stroke: none)
  content((mid_ap_x, mid_ap_y), text(fill: blue, size: 14pt, [5]))

  // 頂点ラベル
  content(A, anchor: "north-east", padding: 5pt, text(fill: black, size: 16pt, [A]))
  content(B, anchor: "north-west", padding: 5pt, text(fill: black, size: 16pt, [B]))
  content(C, anchor: "south-west", padding: 5pt, text(fill: black, size: 16pt, [C]))
  content(D, anchor: "south-east", padding: 5pt, text(fill: black, size: 16pt, [D]))
  content(P, anchor: "north", padding: 5pt, text(fill: black, size: 16pt, [P]))
})
)

まとめ

この記事では、TypstのCeTZパッケージを使って幾何学的な図形を描画する方法を解説しました。特に以下のテクニックを紹介しました：

座標系を使った点の配置
line()を使った線分の描画
ベクトルの正規化による任意角度での直角記号描画
content()とanchorを使ったテキストラベルの配置
rect()を使った背景の描画

CeTZパッケージは、数学的な図形の描画において非常に強力なツールです。座標を計算し、関数を定義することで、複雑な図形も正確に描画できます。

ぜひ、皆さんもCeTZを使って美しい図形を描いてみてください！

GitHubで編集を提案

Discussion

iwkjosec

いくつか気になった点があるのでコメントさせて頂きます。
正方形の描画はline(A, B, C, D, close: true)とすべきです。

line(A, B, C, D, A)で描いた正方形はよく見るとAの角が欠けています。
ベクトルに対する操作はcetz.vector.*にいくつか定義されていて、normがあるのでnormalizeを自前で定義する必要はないです。中点もlerpで計算できます。

(px + u_pq.at(0) * psize, py + u_pq.at(1) * psize)のようなコードもaddやscaleでベクトルを分解せずに書けると思います。
直角記号はcetz.angle.right-angleが使えます。
let px = P.at(0)
let py = P.at(1)
こういう分解は以下のように書けます。
let (px, py) = P
余談

#set pageのpaper、height、widthはデフォルトなので指定しなくてよいのでは･･･？

清水団

ありがとうございます。
ご指摘いただいた中で，直角記号だけは確か，うまく表示できなかったと思うので，こちらはもう一度試してみたいと思います。

iwkjosec

これで(角Aの欠け以外は)同じ図を表示できます

#import "@preview/cetz:0.4.2"
#figure(
  cetz.canvas(length: 2cm, {
    import cetz.draw: content, line, rect-around
    import cetz.angle: right-angle

    let r58 = calc.sqrt(58)

    let A = (0, 0)
    let B = (r58, 0)
    let C = (r58, r58)
    let D = (0, r58)
    let P = (r58 - 21 / r58, r58 - 49 / r58)
    let Q = (49 / r58, r58 - 21 / r58)
    let R = (21 / r58, 49 / r58)
    let S = (r58 - 49 / r58, 21 / r58)

    // 矩形ABCD
    line(A, B, C, D, close: true, stroke: 2pt)

    line(C, P, stroke: 2pt)
    line(D, Q, stroke: 2pt)
    line(A, R, stroke: 2pt)
    line(B, S, stroke: 2pt)

    // AP を結ぶ線
    line(A, P, stroke: 2pt)

    // ABCD の直角記号
    right-angle(A, B, D, radius: 0.2, label: none)
    right-angle(B, C, A, radius: 0.2, label: none)
    right-angle(C, D, B, radius: 0.2, label: none)
    right-angle(D, A, C, radius: 0.2, label: none)

    // PQRS の直角記号
    right-angle(P, B, C, radius: 0.2, label: none)
    right-angle(Q, C, D, radius: 0.2, label: none)
    right-angle(R, D, A, radius: 0.2, label: none)
    right-angle(S, A, B, radius: 0.2, label: none)

    // 各辺の中点に長さを表示（白い背景付き）
    let edge-length(x, y, n) = {
      let m = cetz.vector.lerp(x, y, 0.5)
      rect-around(m, padding: 0.2, fill: white, stroke: none)
      content(m, text(fill: blue, size: 14pt, n))
    }
    edge-length(P, Q, [4])
    edge-length(Q, R, [4])
    edge-length(R, S, [4])
    edge-length(S, P, [4])
    edge-length(A, S, [3])
    edge-length(B, P, [3])
    edge-length(C, Q, [3])
    edge-length(D, R, [3])
    edge-length(A, P, [5])

    // 頂点ラベル
    content(A, anchor: "north-east", padding: 5pt, text(size: 16pt)[A])
    content(B, anchor: "north-west", padding: 5pt, text(size: 16pt)[B])
    content(C, anchor: "south-west", padding: 5pt, text(size: 16pt)[C])
    content(D, anchor: "south-east", padding: 5pt, text(size: 16pt)[D])
    content(P, anchor: "north", padding: 5pt, text(size: 16pt)[P])
  }),
)