📐
TypstのCeTZパッケージで座標平面に円と直線を描く：三角関数の最大・最小問題

2025/12/06に公開
!この記事はTypst Advent Calendar 2025の12月6日の記事です。

 はじめにX（旧Twitter）で@tekkinohoさんから面白い三角関数の最大・最小問題が投稿されました：
!0 \leq \theta \leq \pi , \sin \theta + \cos \theta \geq \frac{1}{2} をみたして，\theta が動くとき，\sin \theta - \cos \theta の値の取りうる値の範囲は？
この記事では、この問題をTypstとCeTZパッケージを使って可視化する方法を詳しく解説します。特に座標平面上に円弧、直線、領域を描画するCeTZパッケージのコードについて丁寧に説明していきます。

 問題と解答の概要まず問題を整理しましょう。
問題: 0 \leq \theta \leq \pi , \sin \theta + \cos \theta \geq \frac{1}{2} をみたして，\theta が動くとき，\sin \theta - \cos \theta の値の取りうる値の範囲は？
解答のアプローチ: x = \cos \theta, y = \sin \theta とおくと、

(\cos \theta, \sin \theta) で (0 \leq \theta \leq \pi) は単位円の上半分（赤い円弧）

x + y \geq \frac{1}{2} は直線より上の領域（水色の領域）

y - x = k とおいて、直線 y = x + k が赤い円弧と共有点を持つような k の範囲を求める
結果は -1 \leq \sin \theta - \cos \theta \leq \frac{\sqrt{7}}{2} となります。
以下がCeTZで作成した図です：

 CeTZパッケージとはCeTZは、Typstで図形を描画するための強力なパッケージです。座標系を使って点を配置し、線や図形を描くことができます。
まず、CeTZパッケージをインポートします：
#import "@preview/cetz:0.4.2"

 CeTZ描画の基本構造CeTZで図形を描くには、cetz.canvas()関数を使用します：
#cetz.canvas(length: 3cm, {
  import cetz.draw: *
  // ここに描画コードを記述
})
length: 3cmは、座標系の単位長さを指定しています。つまり、座標1が実際には3cmとして描画されます。

 座標軸の描画まず座標軸を描きます：
// 座標軸
line((-1.5, 0), (1.5, 0), stroke: (paint: black, thickness: 1pt), name: "x-axis")
line((0, -1.5), (0, 1.5), stroke: (paint: black, thickness: 1pt), name: "y-axis")

// 軸ラベル
content((1.5, -0.15), anchor: "north", text(size: 14pt, $x$))
content((-0.15, 1.5), anchor: "east", text(size: 14pt, $y$))
content((-0.15, -0.15), anchor: "north-east", text(size: 14pt, $O$))
line()関数で2点を結ぶ線分を描きます。strokeパラメータで線の色と太さを指定します。content()関数でテキストを配置し、anchorパラメータで配置位置を調整します。

 円弧の描画
 単位円の上半分（赤い円弧）単位円の上半分を描画します：
arc((0, 0), start: 0deg, stop: 180deg, radius: 1, stroke: (paint: red, thickness: 2.5pt), name: "arc-red")
arc()関数は円弧を描きます：
第1引数: 中心座標 (0, 0)

start: 開始角度（度数法）

stop: 終了角度（度数法）

radius: 半径

stroke: 線のスタイル
角度は右向き（x軸の正方向）を0度として、反時計回りに増加します。

 条件を満たす部分（青い円弧）直線 x + y = \frac{1}{2} より左側の円弧を青で描画します：
arc((0, 0), start: 120deg, stop: 180deg, radius: 1, stroke: (paint: blue, thickness: 2.5pt), name: "arc-blue")
120度から180度までの円弧を描くことで、条件 x + y \geq \frac{1}{2} を満たす範囲を強調します。

 直線の描画複数の直線を描画します：
// 直線 x + y = 1/2（黒線）
line((-0.5, 1), (1, -0.5), stroke: (paint: black, thickness: 1.5pt))

// 直線 y - x = √2（青線）
line((-0.5, calc.sqrt(2) - 0.5), (0.5, calc.sqrt(2) + 0.5), stroke: (paint: blue, thickness: 1.5pt))

// 直線 y - x = -1（紫線）
line((-0.5, -1.5), (1.2, 0.2), stroke: (paint: purple, thickness: 1.5pt))

// 直線 y - x = √7/2（緑線）
let k_max = calc.sqrt(7) / 2
line((-0.5, k_max - 0.5), (0.5, k_max + 0.5), stroke: (paint: green, thickness: 1.5pt))
それぞれの直線は異なる色で描画され、視覚的に区別しやすくなっています。calc.sqrt()関数で平方根を計算できます。

 領域の塗りつぶし条件 x + y \geq \frac{1}{2} を満たす領域を水色で塗りつぶします：
// 水色の領域（x + y ≥ 1/2 の部分）
// 多角形で近似
let pts = ()
for i in range(0, 61) {
  let angle = i * 3deg
  let x = calc.cos(angle)
  let y = calc.sin(angle)
  if x + y >= 0.48 {  // 少し余裕を持たせる
    pts.push((x, y))
  }
}
// 直線との交点を追加
let x1 = (1 - calc.sqrt(7)) / 4
let y1 = (1 + calc.sqrt(7)) / 4
pts.push((x1, y1))
pts.push((0.5, 0))

// 塗りつぶし
if pts.len() > 2 {
  line(..pts, close: true, fill: rgb(200, 240, 255, 150), stroke: none)
}
このコードのポイント：

forループで円弧上の点を3度ずつ計算
条件 x + y \geq 0.48 を満たす点のみを配列に追加（0.5ではなく0.48にして少し余裕を持たせる）
直線との交点を手動で追加

line(..pts, close: true)で多角形を閉じて描画

fillパラメータで塗りつぶしの色を指定（RGBA形式）

stroke: noneで輪郭線を描画しない
rgb(200, 240, 255, 150)は、R=200, G=240, B=255, A=150（透明度）の水色を表します。

 端点の描画とラベル重要な点を円で強調し、ラベルを付けます：
// 端点
circle((1, 0), radius: 0.05, fill: blue, stroke: none)
let x_left = (1 - calc.sqrt(7)) / 4
let y_left = (1 + calc.sqrt(7)) / 4
circle((x_left, y_left), radius: 0.05, fill: blue, stroke: none)

// 端点のラベル
content((1, 0), anchor: "north-west", padding: 3pt, text(size: 12pt, $(1, 0)$))
content((x_left, y_left), anchor: "south-east", padding: 3pt, text(size: 10pt, $((1-sqrt(7))/4, (1+sqrt(7))/4)$))
circle()関数で小さな円を描き、fillで塗りつぶします。content()でラベルを配置し、anchorで位置を調整します。

 図全体のコード最後に、完全なコードを示します：
#set page(
paper: "a4",
height: 297mm,
width: 210mm,
margin: (x: 1.5cm, y: 1.5cm),
)

#set par(
  justify: true,
  leading: 1em,
)

#set text(
  font: ("New Computer Modern","BIZ UDPMincho")
)

#show regex("[\p{scx:Han}\p{scx:Hira}\p{scx:Kana}]"): set text(font: "BIZ UDPGothic")
#set text(lang: "ja")

#set enum(numbering: "(1)",)

#import "@preview/colorful-boxes:1.4.2": *

#let my_block(back_color, frame_color, title_color, content_color, title, content) = {
  block(width:auto,radius: 4pt, stroke: back_color + 3pt)[
    #block(width: 100%,fill: back_color, inset: (x: 20pt, y: 5pt), below: 0pt)[#text(title_color,font: ("New Computer Modern","BIZ UDPMincho"))[#title]]
   #block(radius: (
    bottom: 3pt,
  ),width: 100%, fill: frame_color, inset: (x: 20pt, y: 10pt))[#text(content_color)[#content]]
  ]
}

#my_block(green.darken(20%),rgb(95%, 100%, 95%) , white, black, [\@tekkinoho さんからの最大・最小の問題], [
  $0 lt.eq theta lt.eq pi$ , $sin theta + cos theta gt.eq 1/2$ をみたして，$theta$ が動くとき，$sin theta - cos theta$ の値の取りうる値の範囲は？
])

#h(5mm)
$x = cos theta$ , $y = sin theta$ とすると

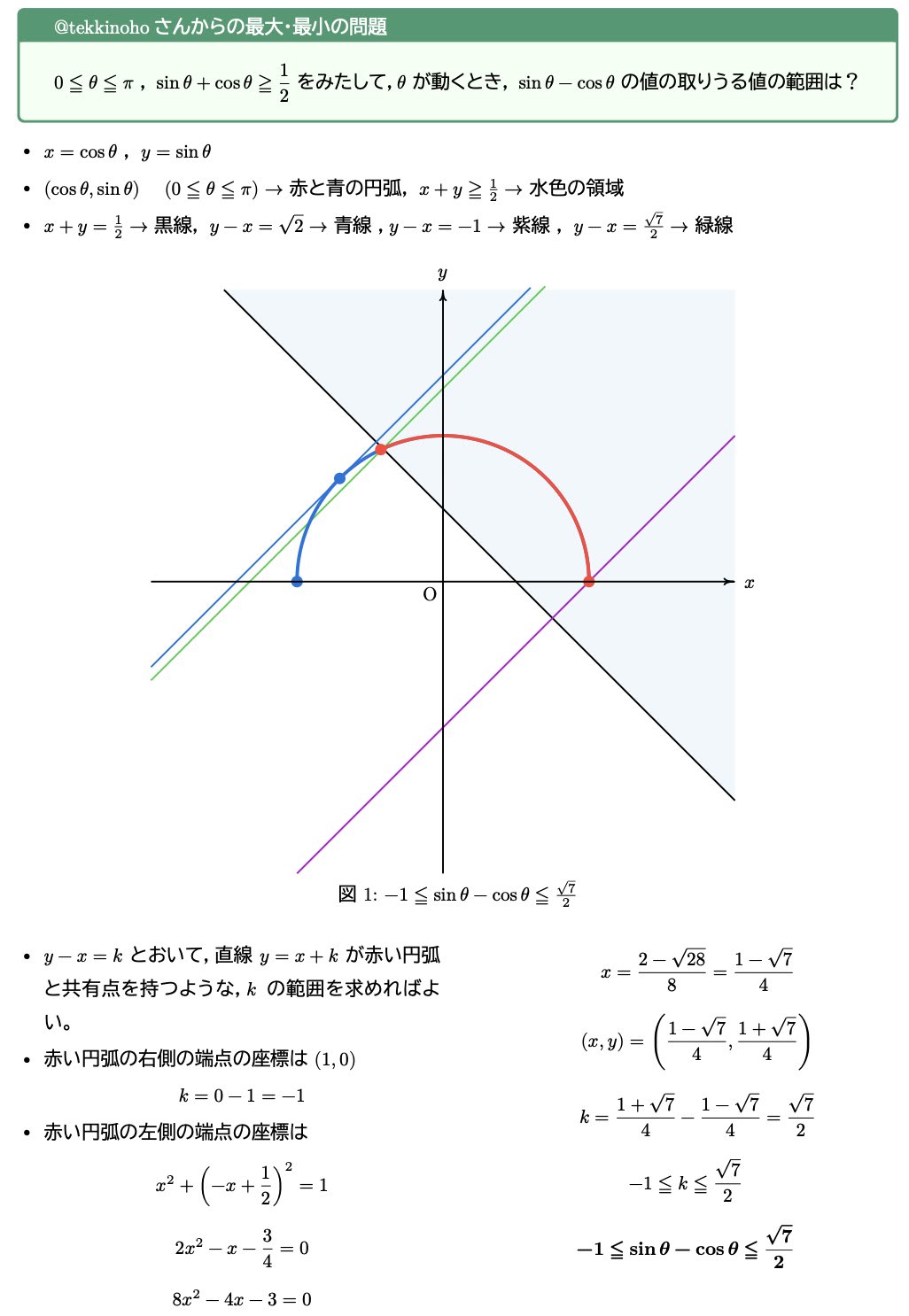
- $(cos theta, sin theta)$ #h(3mm) $(0 lt.eq theta lt.eq pi)$ → 赤と青の円弧，$x + y gt.eq 1/2$ → 水色の領域
- $x + y = 1/2$ → 黒線，$y - x = sqrt(2)$ → 青線，$y - x = -1$ → 紫線，$y - x = sqrt(7)/2$ → 緑線

$y - x = k$ とおいて，直線 $y = x + k$ が赤い円弧と共有点を持つような，$k$ の範囲を求めればよい。

- 赤い円弧の右側の端点の座標は $(1, 0)$
  $ k = 0 - 1 = -1 $

- 赤い円弧の左側の端点の座標は
  $ x^2 + (-x + 1/2)^2 = 1 $
  $ 2x^2 - x - 3/4 = 0 $
  $ 8x^2 - 4x - 3 = 0 $
  $ x = (2 - sqrt(28))/8 = (1 - sqrt(7))/4 $
  $ (x, y) = ((1 - sqrt(7))/4, (1 + sqrt(7))/4) $
  $ k = (1 + sqrt(7))/4 - (1 - sqrt(7))/4 = sqrt(7)/2 $

$ -1 lt.eq k lt.eq sqrt(7)/2 $

$ therefore -1 lt.eq sin theta - cos theta lt.eq sqrt(7)/2 $

#import "@preview/cetz:0.4.2"
#figure(
cetz.canvas(length: 3cm, {
  import cetz.draw: *

  // 座標軸
  line((-1.5, 0), (1.5, 0), stroke: (paint: black, thickness: 1pt), name: "x-axis")
  line((0, -1.5), (0, 1.5), stroke: (paint: black, thickness: 1pt), name: "y-axis")

  // 軸ラベル
  content((1.5, -0.15), anchor: "north", text(size: 14pt, $x$))
  content((-0.15, 1.5), anchor: "east", text(size: 14pt, $y$))
  content((-0.15, -0.15), anchor: "north-east", text(size: 14pt, $O$))

  // 単位円（赤い円弧：0 ≤ θ ≤ π）
  arc((0, 0), start: 0deg, stop: 180deg, radius: 1, stroke: (paint: red, thickness: 2.5pt), name: "arc-red")

  // 青い円弧（直線 x + y = 1/2 より左側の部分）
  arc((0, 0), start: 120deg, stop: 180deg, radius: 1, stroke: (paint: blue, thickness: 2.5pt), name: "arc-blue")

  // 直線 x + y = 1/2（黒線）
  line((-0.5, 1), (1, -0.5), stroke: (paint: black, thickness: 1.5pt))

  // 直線 y - x = √2（青線）
  line((-0.5, calc.sqrt(2) - 0.5), (0.5, calc.sqrt(2) + 0.5), stroke: (paint: blue, thickness: 1.5pt))

  // 直線 y - x = -1（紫線）
  line((-0.5, -1.5), (1.2, 0.2), stroke: (paint: purple, thickness: 1.5pt))

  // 直線 y - x = √7/2（緑線）
  let k_max = calc.sqrt(7) / 2
  line((-0.5, k_max - 0.5), (0.5, k_max + 0.5), stroke: (paint: green, thickness: 1.5pt))

  // 水色の領域（x + y ≥ 1/2 の部分）
  // 多角形で近似
  let pts = ()
  for i in range(0, 61) {
    let angle = i * 3deg
    let x = calc.cos(angle)
    let y = calc.sin(angle)
    if x + y >= 0.48 {  // 少し余裕を持たせる
      pts.push((x, y))
    }
  }
  // 直線との交点を追加
  let x1 = (1 - calc.sqrt(7)) / 4
  let y1 = (1 + calc.sqrt(7)) / 4
  pts.push((x1, y1))
  pts.push((0.5, 0))

  // 塗りつぶし
  if pts.len() > 2 {
    line(..pts, close: true, fill: rgb(200, 240, 255, 150), stroke: none)
  }

  // 端点
  circle((1, 0), radius: 0.05, fill: blue, stroke: none)
  let x_left = (1 - calc.sqrt(7)) / 4
  let y_left = (1 + calc.sqrt(7)) / 4
  circle((x_left, y_left), radius: 0.05, fill: blue, stroke: none)

  // 端点のラベル
  content((1, 0), anchor: "north-west", padding: 3pt, text(size: 12pt, $(1, 0)$))
  content((x_left, y_left), anchor: "south-east", padding: 3pt, text(size: 10pt, $((1-sqrt(7))/4, (1+sqrt(7))/4)$))
})
,caption: [$-1 lt.eq sin theta - cos theta lt.eq sqrt(7)/2$]
)

 CeTZの主要機能まとめこの記事で紹介したCeTZの主要機能をまとめます：

 基本図形
line(点1, 点2, ...): 線分・折れ線を描画

arc(中心, start: 角度, stop: 角度, radius: 半径): 円弧を描画

circle(中心, radius: 半径): 円を描画

 スタイル設定
stroke: 線のスタイル（色、太さ）
stroke: (paint: red, thickness: 2pt)


fill: 塗りつぶしの色

fill: rgb(200, 240, 255, 150)（RGBA形式）


stroke: none: 輪郭線を描画しない

 テキスト配置
content(座標, text(...)): テキストを配置

anchor: テキストの基準位置（"north", "south", "east", "west"など）

padding: テキストと基準点の間隔

 計算機能
calc.sqrt(x): 平方根

calc.cos(angle): コサイン

calc.sin(angle): サイン

 制御構造
let 変数 = 値: 変数定義

for i in range(開始, 終了): forループ

if 条件 { ... }: 条件分岐

 まとめこの記事では、TypstのCeTZパッケージを使って座標平面上に円弧、直線、領域を描画する方法を解説しました。特に以下のテクニックを紹介しました：

arc()を使った円弧の描画

line()を使った直線の描画
forループと条件分岐を使った領域の塗りつぶし

circle()を使った点の強調

content()とanchorを使ったテキストラベルの配置
CeTZパッケージは、数学的な図形の描画において非常に強力なツールです。座標を計算し、条件分岐やループを使うことで、複雑な図形も正確に描画できます。
三角関数の最大・最小問題のような数学の問題を可視化することで、理解が深まります。ぜひ、皆さんもCeTZを使って美しい数学の図形を描いてみてください！
GitHubで編集を提案
はじめに

問題と解答の概要

CeTZパッケージとは

CeTZ描画の基本構造

座標軸の描画

円弧の描画

単位円の上半分（赤い円弧）

条件を満たす部分（青い円弧）

直線の描画

領域の塗りつぶし

端点の描画とラベル

図全体のコード

CeTZの主要機能まとめ

基本図形

スタイル設定

テキスト配置

計算機能

制御構造

まとめ

Discussion
