Julia言語でクラスタリング
この記事は以下のAdvent Calendarの12月11日の記事です:
はじめに
クラスタリングにちょっと興味があって,取り組んでみることにしました。
k-means 法(k=2)でやってみることにしました。
k-means 法(k=2)
k-means法(k平均法)は、データの重心を求めることでk個のクラスタ(集団)に分類する、代表的なクラスタリング手法です。教師なし学習に分類され、事前にラベル付けする必要がありません。
- k = 2 なら、「2つのグループに分けたい」という意味
- ポイントは、各グループの重心(セントロイド)を計算しながら繰り返し分類すること
アルゴリズムの手順
k-means法は以下の4ステップで実行されます:
ステップ1:初期化
k個のクラスタ中心(セントロイド)を適当に決めます。
- 例:ランダムに選んだk個のデータ点を初期中心とする
- より良い結果を得るには k-means++ という初期化手法が有効
ステップ2:割り当て(Assignment)
各データ点を、最も近いクラスタ中心に割り当てます。
- 距離はユークリッド距離(2点間の直線距離)を使用
- 数式:
\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}
ステップ3:重心の更新(Update)
各クラスタに割り当てられたデータ点の平均位置を計算し、新しいクラスタ中心とします。
- 例:クラスタ1に点A(2,3)と点B(4,5)が入った場合
- 新しい中心 =
((2+4)/2, (3+5)/2) = (3, 4)
ステップ4:収束判定
ステップ2と3を繰り返し、以下のいずれかの条件で終了します:
- 各点の割り当てられるクラスタが変化しなくなった
- クラスタ中心が動かなくなった
- 指定した最大反復回数に達した
この状態を収束といいます。
メリット
- アルゴリズムが単純で理解しやすい
- 計算負荷が少なく、大規模データにも適用可能
- 距離計算のみで済むため高速
デメリット
- クラスタ数kを事前に決める必要がある
- 初期値依存性:初期中心の選び方で結果が変わる(局所最適解に陥りやすい)
- 球状のクラスタ以外の形状にはうまく対応できない
初期値問題への対策
- k-means++を使う:できるだけ離れた点を初期中心に選ぶ改良版
- 複数回実行して最良の解を採用:異なる初期値で複数回実行し、最もコスト(クラスタ内距離の合計)が小さい結果を選ぶ
Juliaでクラスタリングを実装していきます。最新バージョン(Julia 1.12.2)でも動作するコードを紹介します。
環境構築
まず必要なパッケージをインストールします:
using Pkg
Pkg.add("Clustering")
Pkg.add("GaussianMixtures")
Pkg.add("Plots")
Pkg.add("Distances")
サンプルデータの作成
40人の数学・英語の点数を生成します。高得点層・中得点層・低得点層の3つのグループを混ぜて、リアルなデータを作ります。
using Random, Statistics, LinearAlgebra
Random.seed!(42)
# 高・中・低の3層
n_high, n_mid, n_low = 12, 16, 12
# 数学の点数
math = vcat(
clamp.(randn(n_high).*6 .+ 85, 0, 100), # 高得点層: 平均85点
clamp.(randn(n_mid ).*8 .+ 65, 0, 100), # 中得点層: 平均65点
clamp.(randn(n_low ).*7 .+ 45, 0, 100) # 低得点層: 平均45点
)
# 英語の点数
eng = vcat(
clamp.(randn(n_high).*6 .+ 83, 0, 100),
clamp.(randn(n_mid ).*8 .+ 62, 0, 100),
clamp.(randn(n_low ).*7 .+ 48, 0, 100)
)
# データ形式の準備
X = Matrix(hcat(math, eng)') # 2×40(Clustering.jl用)
data = hcat(math, eng) # 40×2(GMM用)
生成されたデータを可視化すると以下のようになります:
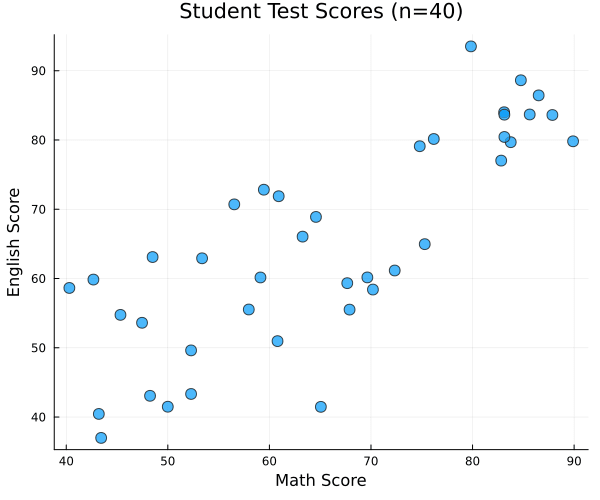
40人の生徒が数学(横軸)と英語(縦軸)のテストを受けた結果です。高得点層・中得点層・低得点層の3つのグループが混在していることがわかります。
k-meansクラスタリングの実装
初期値依存性の問題を解決するため、複数回実行して最良の解を採用する関数を実装します。
using Clustering
function best_kmeans(X, k; trials=20, init=:kmpp, maxiter=100, tol=1e-6, seed=0)
best_R = nothing
best_cost = Inf
for t in 1:trials
# 各試行で異なる初期値を使う
rng_t = MersenneTwister(seed + t)
R = kmeans(X, k; init=init, maxiter=maxiter, tol=tol, rng=rng_t)
if R.totalcost < best_cost
best_cost = R.totalcost
best_R = R
end
end
return best_R
end
# k=3でクラスタリング実行
k = 3
R_km = best_kmeans(X, k; trials=20, init=:kmpp, seed=1)
labels_km = R_km.assignments
centers_km = R_km.centers
その他のクラスタリング手法との比較
k-means以外にも代表的なクラスタリング手法があります。それぞれの特徴を見てみましょう。
DBSCANによるクラスタリング
DBSCANは密度ベースのクラスタリング手法で、ノイズ(外れ値)を検出できるのが特徴です。
using Distances
# 距離行列を作成してDBSCANに渡す
D_db = pairwise(Euclidean(), X, dims=2) # 40×40
db = dbscan(D_db, 8.0, 3) # eps=8.0, minpts=3
labels_db = db.assignments # ノイズは 0
階層型クラスタリング
階層型はデータを段階的にグループ化していく手法です。樹形図(デンドログラム)で可視化できます。
D_hc = pairwise(Euclidean(), X, dims=2)
hc = hclust(D_hc; linkage=:ward)
labels_hc = cutree(hc; k=k)
GMMによるクラスタリング
GMM(Gaussian Mixture Model:ガウス混合モデル)は、確率的なクラスタリング手法です。
using GaussianMixtures
gmm = GMM(k, data; method=:kmeans, kind=:diag, nIter=30)
tmp = gmmposterior(gmm, data)
resp = tmp isa Tuple ? tmp[1] : tmp # 後方互換性のための処理
labels_gmm = [argmax(resp[i, :]) for i in 1:size(data,1)]
μ = gmm.μ
centers_gmm = size(μ,1) == k ? μ : μ' # k×2 に整形
4つの手法を比較可視化
using Plots
# 保存先ディレクトリの作成(存在しない場合)
isdir("images") || mkdir("images")
pal = [:red, :blue, :green, :orange, :purple]
# k-means
plt1 = scatter(math, eng; group=labels_km, palette=pal[1:k],
xlabel="Math", ylabel="English", title="k-means (best of 20, k=$k)", legend=false)
scatter!(plt1, centers_km[1,:], centers_km[2,:];
markershape=:x, color=:black, markersize=10)
# DBSCAN
plt2 = scatter(math, eng; group=labels_db, palette=pal,
xlabel="Math", ylabel="English", title="DBSCAN (eps=8, minpts=3)", legend=false)
# 階層型
plt3 = scatter(math, eng; group=labels_hc, palette=pal[1:k],
xlabel="Math", ylabel="English", title="Hierarchical (Ward, cut k=$k)", legend=false)
# GMM
plt4 = scatter(math, eng; group=labels_gmm, palette=pal[1:k],
xlabel="Math", ylabel="English", title="GMM (k=$k)", legend=false)
scatter!(plt4, centers_gmm[:,1], centers_gmm[:,2];
markershape=:x, color=:black, markersize=10)
# 2×2レイアウトで表示・保存
p = plot(plt1, plt2, plt3, plt4; layout=(2,2), size=(900,700))
savefig(p, "images/clustering_comparison.png")
実行結果は以下のようになります:
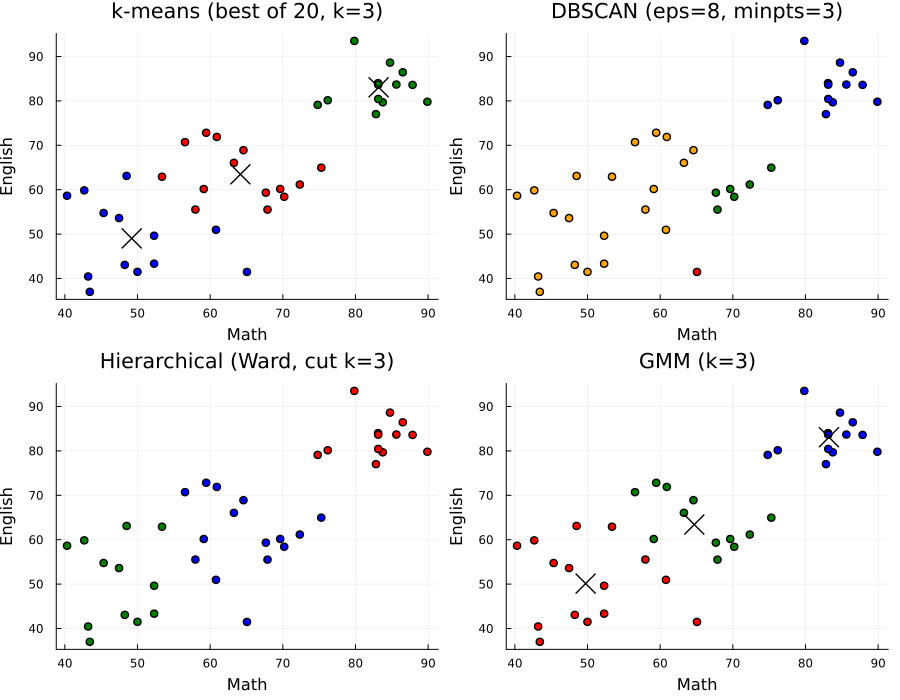
4つの異なるクラスタリング手法でそれぞれ異なる結果が得られていることがわかります。各手法の特徴:
- k-means: 明確な3つのクラスタに分類。×印はクラスタ中心を示す
- DBSCAN: 密度ベース。外れ値を検出可能(グレーの点)
- 階層型(Hierarchical): 段階的にグループ化。Wardリンケージを使用
- GMM: 確率的アプローチ。各点がどのクラスタに属する確率を計算
クラスタリング結果の解釈
色の意味について
プロットの色は**点数の高低ではなく「クラスタ番号」**を表します。重要なポイント:
- 番号や色の割当自体に本質的意味はない(実行ごとに変わる可能性あり)
- ×印(中心)に一番近いクラスタに割り当てられる
- クラスタ境界は「中心間の垂直二等分線」に相当するため、中心付近でも境界の反対側なら別色になることがある
初期中心による結果の違い
k-meansは局所最適解に収束するため、初期中心の選び方で最終クラスタが変わることがあります。
対策:
- k-means++(init=:kmpp) を使う
-
複数回実行して最良の解を採用する(上記の
best_kmeans関数)
実装時の注意点
1. 乱数シードの管理
k-meansで複数回試行する際は、各試行で異なる乱数シードを使いましょう。同じシードを使い回すと、同じ初期値から始まってしまいます。
# 良い例
for t in 1:trials
rng_t = MersenneTwister(seed + t) # 異なるシード
R = kmeans(X, k; rng=rng_t)
end
2. パッケージバージョンの違い
GaussianMixtures.jlやClustering.jlはバージョンによって関数の挙動が異なる場合があります。複数バージョンに対応するには、条件分岐を使うと良いでしょう。
# 戻り値の型をチェック
resp = tmp isa Tuple ? tmp[1] : tmp
まとめ
- k-meansは代表的なクラスタリング手法で、中心との距離でグループ分け
- 初期値依存性があるため、複数回実行して最良解を選ぶのが推奨
- 複数の手法を比較することで、データの特性に合った手法を選べる
- Julia 1.12.2では、乱数シード管理やディレクトリ確認などの基本的な注意点を押さえることが重要
Discussion