🍣

二項分布の半整数補正をJuliaで確認

2024/01/05に公開1件

はじめに

高校数学Bの「統計的な推測」の分野で，@kobayashi__renさんから次のようなポストがありました。

なんとなく，「Juliaで計算してみよう！」と思いスタートです。

問題と解答

問題を確認します。

まずは普通に解いてみます。

解答

$R$ は正規分布 $N(0.5,\,(1/20)^2)$ に近似的に従います。

$Z=20(R-0.5)$ とおくと， $Z$ は $N(0,\,1)$ に従います。正規分布表を見て

P\left(\left|R-\dfrac12\right|\leqq 0.05\right)=P(\left|Z\right|\leqq 1)=0.3413\times 2=0.6826

解答はこうなると思いますが，天下り的ですね。

もう少し丁寧に

もう少し丁寧に作ってみます。

表の出る回数を $X$ とすると， $R=\dfrac{X}{n}=\dfrac{X}{100}$

$\left|R-\dfrac12\right|\leqq 0.05$ より，

\left|\dfrac{X}{100}-\dfrac12\right|\leqq 0.05

\therefore \left|X-50\right|\leqq 5

\therefore 45\leqq X\leqq 55

$P\left( 45\leqq X\leqq 55\right)$ を求めます。 $X$ は二項分布 $Bin(100,0.5)$ に従います。

$n=100$ は十分大きいので， $X$ は正規分布に近似できます。

Bin(n,\,p)\sim N(np,\,npq)

Bin(100,\,0.5)\sim N(100\times 0.5,\,100\times 0.5\times 0.5)=N(50,\,5^2)

$Z=\dfrac{X-50}{5}$ とおくと， $Z=N(0,1)$ となります。

$\left|X-50\right|\leqq 5$ より，

\therefore\left|Z\right|\leqq 1

Juliaの累積分布関数cdfを用いて

using Distributions # 分布パッケージ

2*(cdf(Normal(),1)-cdf(Normal(),0))

0.6826894921370861

\therefore P\left(\left|z\right|\leqq 1\right)=0.6826894921370861

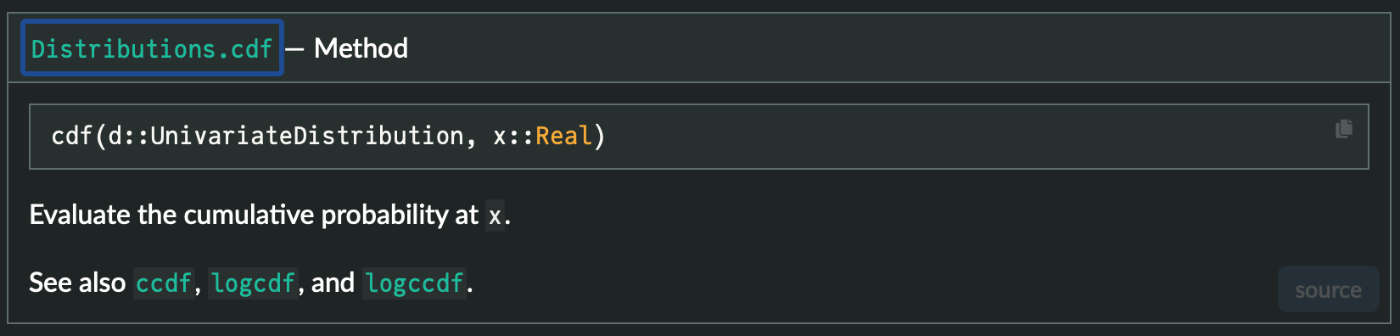
`Julia`の累積分布関数`cdf`

Juliaの累積分布関数cdfは分布パッケージDistributions.jlに入っています。
また，このDistributions.jlでは正規分布Normalや二項分布Binomialなど様々な分布が利用できます。

Distributions.jlパッケージ

累積分布関数cdf

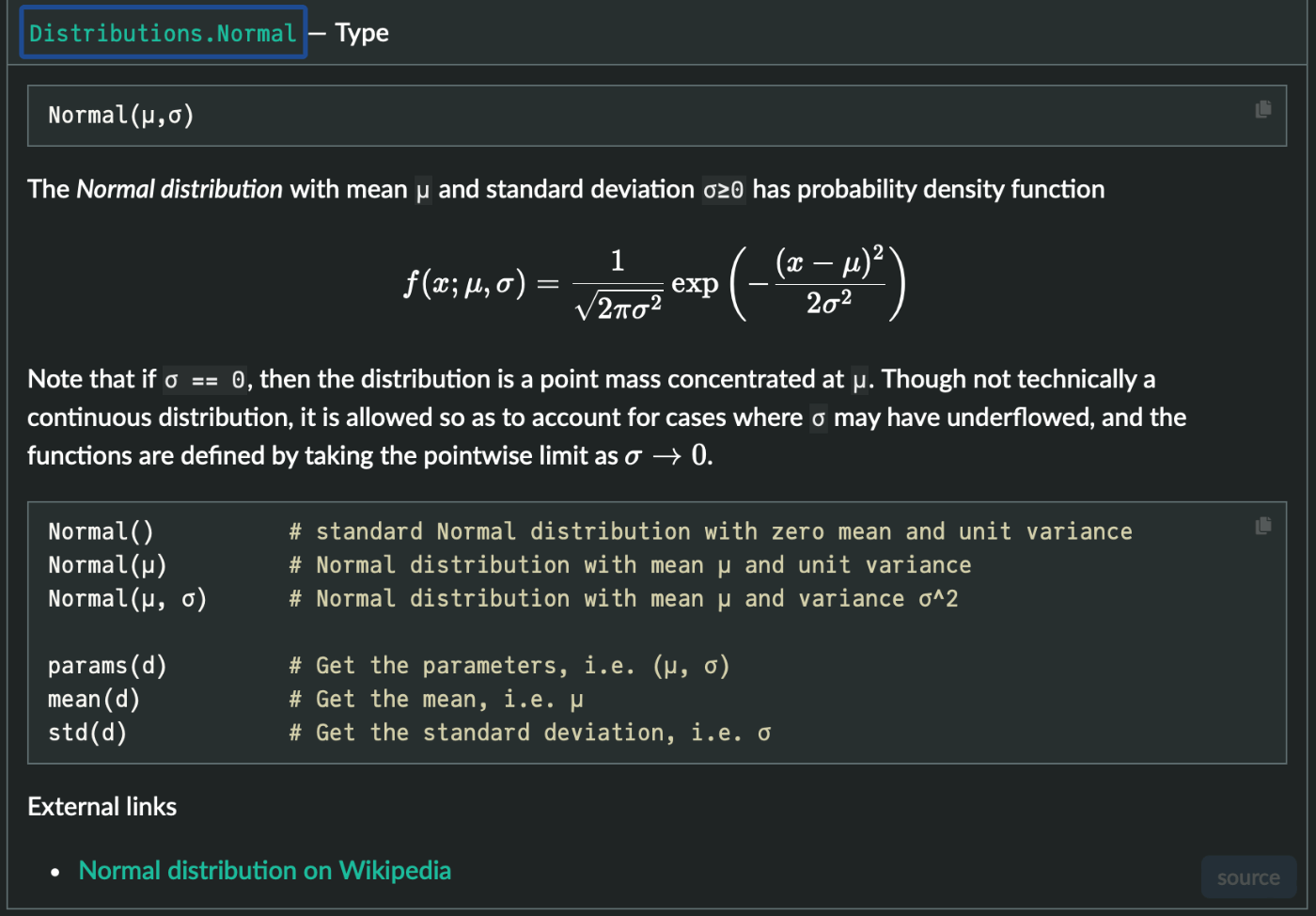
正規分布Normal

二項分布Binomial

二項分布は正規分布に近似できるのか？

「 $n=100$ のとき，二項分布は正規分布に近似できるのか?」です。いろいろ基準はありますが，とりあえず，グラフを書いてみました。分布パッケージDistributions.jlに加えて，統計プロットパッケージStatsPlots.jlを利用します。

using StatsPlots　# 統計プロットパッケージ

dist1 = Binomial(100,0.5) # 二項分布B(100,0.5)
dist2 = Normal(50,sqrt(25)) # 正規分布N(50,5²)

plot(dist1 , label = "Binomial(100,0.5)")
plot!(dist2 , label = "Normal(50,5²)")

とてもいい感じです。近似してよさそうです。

今の時代，正規分布表まで戻らなくてもいいのではないか？

高校数学Bの教科書では、「標準正規分布とその表から値を求める」というのが流れです。しかし，今はPCなどで、誰もが二項分布のままでも確率の計算が容易にできます。「正規分布表まで戻らなくてもいいのではないか？」 となんとなく思ってきました。累積分布関数cdfも標準正規分布 $N(0,1)$ 以外にも利用できます。そこで，幾つかの段階で確率を求めてみることにしました。

正規分布 $N(50,\,5^2)$ で確率を求める

dist2 = Normal(50,sqrt(25)) # 正規分布N(50,5²)

cdf(dist2,55)-cdf(dist2,45)

0.6826894921370861

P(45\leqq X\leqq 55)=0.6826894921370861

もちろん大丈夫。

二項分布 $Bin(100,\,0.5)$ で確率を求める（その1）

dist1 = Binomial(100,0.5) # 二項分布B(100,0.5)

cdf(dist1,55)-cdf(dist1,45)

0.6802726792997346

P(45\leqq X\leqq 55)=0.6802726792997346

これは，二項分布を連続的に拡張して累積分布関数を考えたもので，これもほぼ同じ値になります。

二項分布 $Bin(100,\,0.5)$ で確率を求める（その2）

（その1）は累積分布関数cdfは連続関数であったので，本来の「離散的な確率」を定義から計算することにしました。数が大きくなるので，BigIntを利用しました。

function f(m,n)
    s::BigInt = 0
    t::BigInt = 100
    r = BigInt(2)^100
    for i = m:n
        s += binomial(t,i)
    end
    s/r
end

f(45,55)

0.728746975926165269296176250211956675803539260631347439581273484066059609176591

P(45\leqq X\leqq 55)=\sum_{k=45}^{55}{}_{100}\text{C}_k\cdot2^{100}=0.7287469759261652

これは，今までの値からずれています。約68%から73%になっています。

半整数補正

𝕏でのやり取り

「ちょっとずれているので，みんなどう考えているんだろう？」と思い，𝕏にポストしました。

すぐに，@kaoru6さんと@Lenqthさんから 「半整数補正というのです」 と教えてもらいました。本当にありがたいです。

Webサイト

その後，Webサイトなどでも確認しました。

Juliaで計算の確認

$45\leqq X\leqq 55$ に半整数補正を行い， $44.5\leqq X \leqq 55.5$ としました。このとき， $|Z|\leqq 1.1$ です。

正規分布表より

P(|Z|\leqq 1.1)=0.3643\times 2=0.7286

$N(0,1)$ の累積分布関数より

2*(cdf(Normal(),1.1)-cdf(Normal(),0))

0.7286678781072347

P(|Z|\leqq 1.1)=0.7286678781072347

$N(50,5^2)$ の累積分布関数より

dist2 = Normal(50,sqrt(25)) # 正規分布N(50,5²)

cdf(dist2,55.5)-cdf(dist2,44.5)

0.7286678781072347

P(44.5\leqq X\leqq 55.5)=0.7286678781072347

$Bin(100,0.5)$ の累積分布関数より

dist1 = Binomial(100,0.5) # 二項分布B(100,0.5)

cdf(dist1,55.5)-cdf(dist1,44.5)

0.7287469759261653

P(44.5\leqq X\leqq 55.5)=0.7287469759261653

どれも，離散的な二項分布で求めた確率とほぼ同じ（73%）となります。

まとめ

$n=100$ でこれだけ違う（68%と73%）のはちょっと気になりました。「補正をすると，より正確に求まる」というのはわかるのですが，これだけ違うと，「高校の数学Bの教科書で補正のことを気にしなくていいのか？」「共通テストなどで確率を正規分布表から求めるとき大丈夫なのか？」 と心配してしまいます。

Discussion

清水団

離散分布を連続分布に直して確率を求めるときに，もともと離散分布であったことを考えると，次のように考えると良さそうです。juliaのDistributions.jlでは二項分布の累積密度関数に正則不完全ベータ関数を利用しているようです。

P(45\leqq X\leqq 55) = P(X\leqq 55)-P(X\leqq 44)

using Distributions

dist1 = Binomial(100,0.5) # 二項分布B(100,0.5)
@show cdf(dist1,55)-cdf(dist1,44);

dist2 = Normal(50,sqrt(25)) # 正規分布N(50,5²)
@show cdf(dist2,55)-cdf(dist2,44);

cdf(dist1, 55) - cdf(dist1, 44) = 0.7287469759261653
cdf(dist2, 55) - cdf(dist2, 44) = 0.7262750758468348

となります。