🎉

ランダムに3点とって鋭角三角形となる確率をJulia で考える。（その2）

2021/08/03に公開

Julia

math

idea

前回の話。

平面に3点をとって，鋭角三角形を作る話の続きです。

次のようにまとめたのですが，やはり，『円の内部の方が確率が高くなるのではないか？』と思い考えました。

『1x1の正方形の内部の27%と単位円の内部の24%の理論値を求めたいです。（調べれば，どこかに載っていそうですが。。。。）また，どうして，単位円よりも正方形の方が鋭角三角形ができやすいのかも不明です。』

円の内部でランダムに3点をとること

「ランダム」はいろいろ考えると難しいのですが，面積比で考えることにします。単位円の内部の部分領域の面積の割合で確率を考えます。例えば，単位円の内部に半径 $\frac12$ の円を作り，その内部に1点とる確率は，単位円の面積は $\pi$ ，半径 $\frac12$ の円の面積は $\frac{\pi}4$ なので，確率は $\frac14=2.5$ となります。

前回，0と1の間の2つの乱数 $r_a$ ， $r_b$ 作り，単位円の内部の点Pを

P(r_a\cos 2r_b \pi,\,r_a\sin 2r_b \pi)

としたのですが，これはランダムとはならず，点が中心にかたまっていることがわかりました。

circle1.jl

D=rand(1000)
R=rand(1000)
M=[R[i]*cos(D[i]*2*pi) for i=1:length(D)]
N=[R[i]*sin(D[i]*2*pi) for i=1:length(D)]

plot(M,N,aspect_ratio=1,st=scatter)

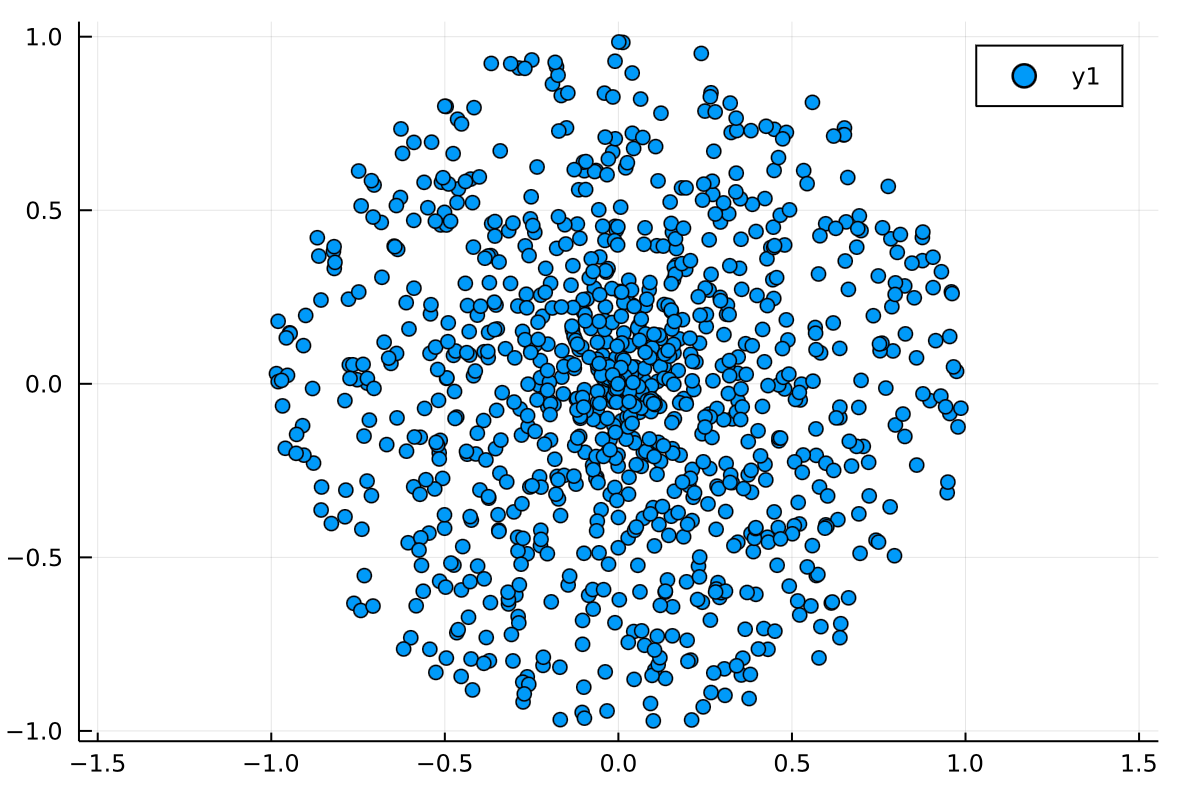
twitterで投げたところ，黒木さん（@genkuroki）からランダムに分布させる修正を教えてもらいました。
半径のところを $\sqrt{r_a}$ 倍するとうまく散らばります。

単位円の内部の点Pを次のように修正しました。

P(\sqrt{r_a}\cos 2r_b \pi,\,\sqrt{r_a}\sin 2r_b \pi)

circle2.jl

D=rand(1000)
R=rand(1000)
M=[sqrt(R[i])*cos(D[i]*2*pi) for i=1:length(D)]
N=[sqrt(R[i])*sin(D[i]*2*pi) for i=1:length(D)]

plot(M,N,aspect_ratio=1,st=scatter)

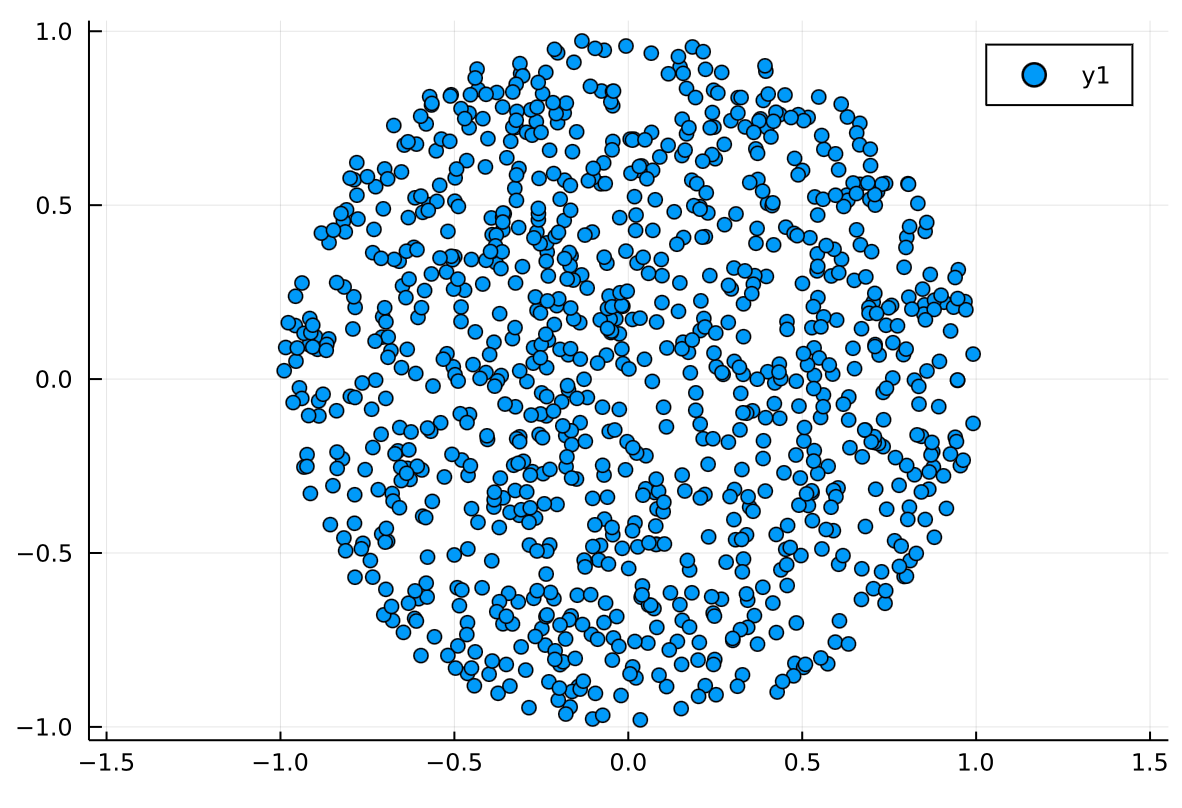
黒木さんから教えてもらったコードでも書いてみました。図が綺麗です！！

circle3.jl

using Plots

function randunitdisk()
    y, x = sincospi(2rand())
    r = √rand()
    r*x, r*y
end

randunitdisk(n) = [randunitdisk() for _ in 1:n]

function randunitdisk2()
    y, x = sincospi(2rand())
    r = rand()
    r*x, r*y
end

randunitdisk2(n) = [randunitdisk2() for _ in 1:n]


plt1=scatter(randunitdisk(2^12); legend=false, msw=0, ms=3, alpha=0.5, size=(500, 500))

plt2=scatter(randunitdisk(2^12); legend=false, msw=0, ms=3, alpha=0.5, size=(500, 500))

plts = plot(plt1, plt2, layout=(2,1), size=(500,500))

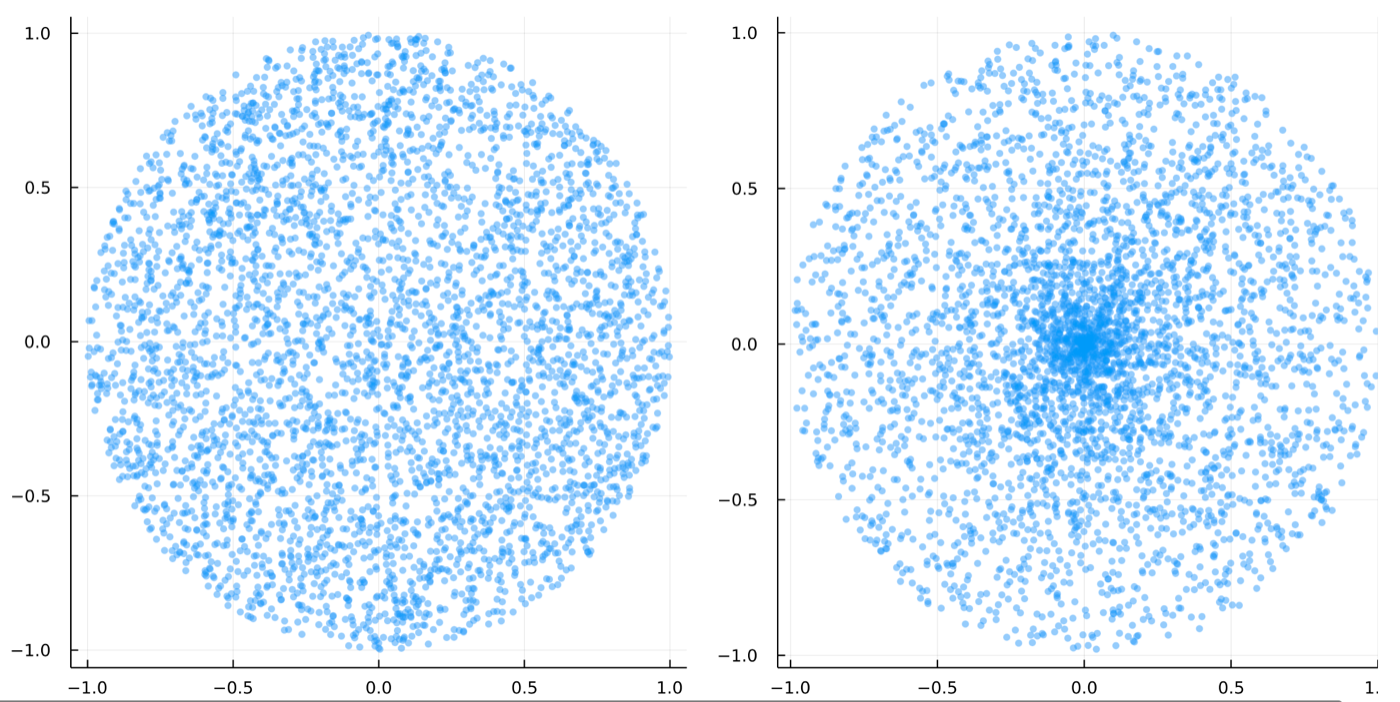
確率の計算

この分布を元に鋭角三角形となる確率を計算します。

prob.jl

n=1000000
k=0
for i=1:n
    b1=rand(2)
    r1=√b1[1]
    a1=[r1*cos(2*π*b1[2]),r1*sin(2*π*b1[2])]
    
    b1=rand(2)
    r1=√b1[1]
    a2=[r1*cos(2*π*b1[2]),r1*sin(2*π*b1[2])]
    
    b1=rand(2)
    r1=√b1[1]
    a3=[r1*cos(2*π*b1[2]),r1*sin(2*π*b1[2])]
   
    x1=a2-a1
    x2=a3-a1
    t1=(x1'*x2)/(sqrt(x1'*x1)*sqrt(x2'*x2))

   x1=a1-a2
    x2=a3-a2
    t2=(x1'*x2)/(sqrt(x1'*x1)*sqrt(x2'*x2))
    
    x1=a1-a3
    x2=a2-a3
    t3=(x1'*x2)/(sqrt(x1'*x1)*sqrt(x2'*x2))
    
    if t1>0.00000001  && t2>0.00000001 && t3>0.00000001
        k+=1
    end
end
println("単位円での確率は",k/n)

単位円での確率は0.280913

まとめ

1x1の正方形の内部の27%に比べて，単位円の内部は28%となりました。やはり，円の方が確率は高いですよね。あとは理論値ですね。

前回の話。

円の内部でランダムに3点をとること

確率の計算

まとめ

Discussion