オンライン整数列大辞典(OEIS)に数列を登録してみた！

今回の内容は2024年12月8日の JuliaLangJa 年末 LT 大会 2024 での発表内容となります。

https://julialangja.connpass.com/event/338390/

また，Julia Advent Calendar 2024の12日目の記事となります。

https://qiita.com/advent-calendar/2024/julia

はじめに

横山 明日希（@asunokibou）さんのXのポストで次のような問題がありました。

https://x.com/asunokibou/status/1858851048510947649

(1)の$\fbox{ア}$〜$\fbox{キ}$に異なる自然数を入れる場合を考えます。

$$\frac{1}{\fbox{ア}}+\frac{2}{\fbox{イ}}+\frac{3}{\fbox{ウ}}+\frac{4}{\fbox{エ}}+\frac{5}{\fbox{オ}}+\frac{6}{\fbox{カ}}+\frac{7}{\fbox{キ}}=7$$

まずは解の1組はちょっと考えるとわかります。

$$\frac{1}{1}+\frac{2}{2}+\frac{3}{3}+\frac{4}{4}+\frac{5}{5}+\frac{6}{6}+\frac{7}{7}=7$$

「他にあるのか？あるとしたら何組あるか？」が気になりました。

Julia言語で調べてみる。

まずは，いつものようにJulia言語で調べてみることにしました。

using Combinatorics

X = [i for i =1:9] |> x->permutations(x,7)
Y = []
for x ∈ X
    if sum(i/x[i] for i=1:7) == 7
        push!(Y,x)
    end
end
Y

49-element Vector{Any}:
[1, 2, 3, 4, 5, 6, 7]
[1, 2, 3, 8, 5, 4, 7]
[1, 2, 4, 3, 5, 8, 6]
[1, 2, 6, 8, 5, 3, 7]
[1, 2, 6, 8, 5, 9, 3]
[1, 2, 9, 3, 6, 4, 7]
[1, 2, 9, 3, 6, 8, 4]
[1, 2, 9, 4, 3, 6, 7]
[1, 2, 9, 6, 5, 3, 7]
[1, 2, 9, 8, 3, 4, 7]
⋮
[4, 8, 9, 2, 5, 3, 6]
[4, 8, 9, 3, 6, 2, 7]
[4, 8, 9, 6, 2, 3, 7]
[6, 1, 4, 3, 5, 8, 7]
[6, 1, 9, 8, 5, 3, 7]
[6, 3, 1, 8, 5, 9, 7]
[6, 4, 9, 2, 5, 3, 7]
[6, 4, 9, 8, 2, 3, 7]
[6, 8, 9, 2, 4, 3, 7]

49通りあるようです。1組確認してみます。

[4, 8, 9, 2, 5, 3, 6]

$$\frac{1}{4}+\frac{2}{8}+\frac{3}{9}+\frac{4}{2}+\frac{5}{5}+\frac{6}{3}+\frac{7}{6}=\frac{1}{4}+\frac{1}{4}+\frac{1}{3}+2+1+2+\frac{7}{6}=7$$

このあと，たむらいつる（@tsatie） さんが $n=6$ のときをチェックしてくれたのですが，何か合わないような報告でした。

https://x.com/tsatie/status/1859552651232309545

$n=6$のとき

$$\frac{1}{\fbox{ア}}+\frac{2}{\fbox{イ}}+\frac{3}{\fbox{ウ}}+\frac{4}{\fbox{エ}}+\frac{5}{\fbox{オ}}+\frac{6}{\fbox{カ}}=6$$

個数を変化させると面白そうだったので，$n=1$から$n=9$まで調べてみました。

$n=1$から$9$のとき

$$\frac{1}{x_1}+\frac{2}{x_2}+\cdots+\frac{n}{x_n}=n$$

using Combinatorics

function c(n)
    X = [i for i =1:9] |> x->permutations(x,n)
    Y = []
    for x ∈ X
        if sum(i/x[i] for i=1:n) == n
            push!(Y,x)
        end
    end
    Y |> length
end

for i = 1:9
    print("$(c(i)),")
end

1,1,3,6,15,38,49,29,1,

とでできました。数列が出てくるとオンライン整数列大辞典(OEIS)で調べたくなります。そして調べてみてると

どうもデータベースになさそうです。（無かったのは初めてです）ということで登録したくなったわけです。

オンライン整数列大辞典(OEIS)に登録

アカウントの作成

まずは，アカウントを作成しました。私の所属は私立の中高なので，その所属で登録することにしました。

シーケンスの登録

数列を登録し，Julia言語での構成も登録しました。

議論開始

すると，数列の説明の文章を直していると，Michel Marcusさんから

「数列はc(n)じゃなくてa(n)がいいよ。この数列はこれで終わり？有限？」

と質問がありました。そこで，数列をc(n)からa(n)に修正して

「シーケンスはc(n)からa(n)に変更しました。このシーケンスは有限ですが、拡張できます。現在、1桁の数字1から9までからn個の整数を選択し、それらを順列に並べることによって形成されています。しかし、これは代わりに1からmまでの数字を選択することで一般化できます。mの値ごとに、有限列が生成できると思います。」

と返しました。

三角形の行で読み取るシーケンス：T(n,k)への変更

今度は，Andrew Howroyd さんからいくつかの提案がありました。

• 「ASCII文字のみにしてください。（特別な下付き文字/上付き文字ではありません）」

• n=1...9からの制限が取り除かれれば、これははるかに良いだろうと考えます。それはどのように数字を変えますか？それ以外の場合は、n がシーケンスの長さであり、数字が 1..k. から選択される三角形 T(n,k) を作成します。 (これはあなたが持っているものに最も近いでしょう)

• 例のセクションは醜いです。（結果のプレゼンテーションを無視することはできません）。プログラムから配列を出力するだけではありません。例：a(3) = 3の解は1/1 + 2/2 + 3/3 = 1/1 + 2/4 + 3/2 = 1/2 + 2/1 + 3/6 = 3です。目に優しいと思います。

なるほど，こうやっていろんな方が指摘してくれるのか。ありがたい！

三角形の行で読み取るシーケンス： $T(n,k)$

• $n$行目には$n$個の数字が並びます。

• $n$行目の$k$番目の数字は

$$\frac{1}{x_1} + \frac{2}{x_2} + \cdots + \frac{k}{x_k} = k$$

となる順列$(x_1,\,x_2,\,...,\,x_k)$の個数です。
ただし，$x_1,\,x_2,\,...,\,x_k$は$1$以上$n$以下の異なる値です。

function T(n,k)
    X = [i for i =1:n] |> x->permutations(x,k)
    Y = []
    for x ∈ X
        if sum(i/x[i] for i=1:k) == k
            push!(Y,x)
        end
    end
    Y |> length
end

for i = 1:9
    print("$(T(9,i)),")
end

1,1,3,6,15,38,49,29,1,

数列が違う！

このあと，Andrew Howroydさんから，びっくりする連絡が来ました。私の提示したシーケンスが合わないということでした。
私が提案したのは

「1,1,3,6,15,38,49,29,1,」

でしたが，

「1,1,3,6,16,40,54,30,1,」

でわないか？との指摘でした。

自分のコードを見直してみたのですが，

i/x[i]は誤差が出るのでは？と思って，i//x[i]として有理数で計算することにしました。

function T(n,k)
    X = [i for i =1:n] |> x->permutations(x,k)
    Y = []
    for x ∈ X
        if sum(i//x[i] for i=1:k) == k
            push!(Y,x)
        end
    end
    Y |> length
end

for i = 1:9
    print("$(T(9,i)),")
end

1,1,3,6,16,40,54,30,1,

確かに違っている。何が足りなかったかは後で検討することにして，まずは修正をしました。

修正するときに，「この数列だったら，すでにOEISに存在するのでは？」と思って，チェックしたのですが，このシーケンスも存在しなかったので，ちょっと安心しました。

DATAの修正，例示の作成

Andrew Howroyd さんが，DATAを三角形の行で読み取るシーケンスに直してくれたり，例示のテーブルを作ってくれたり，PARIのコードを書いてくれました。

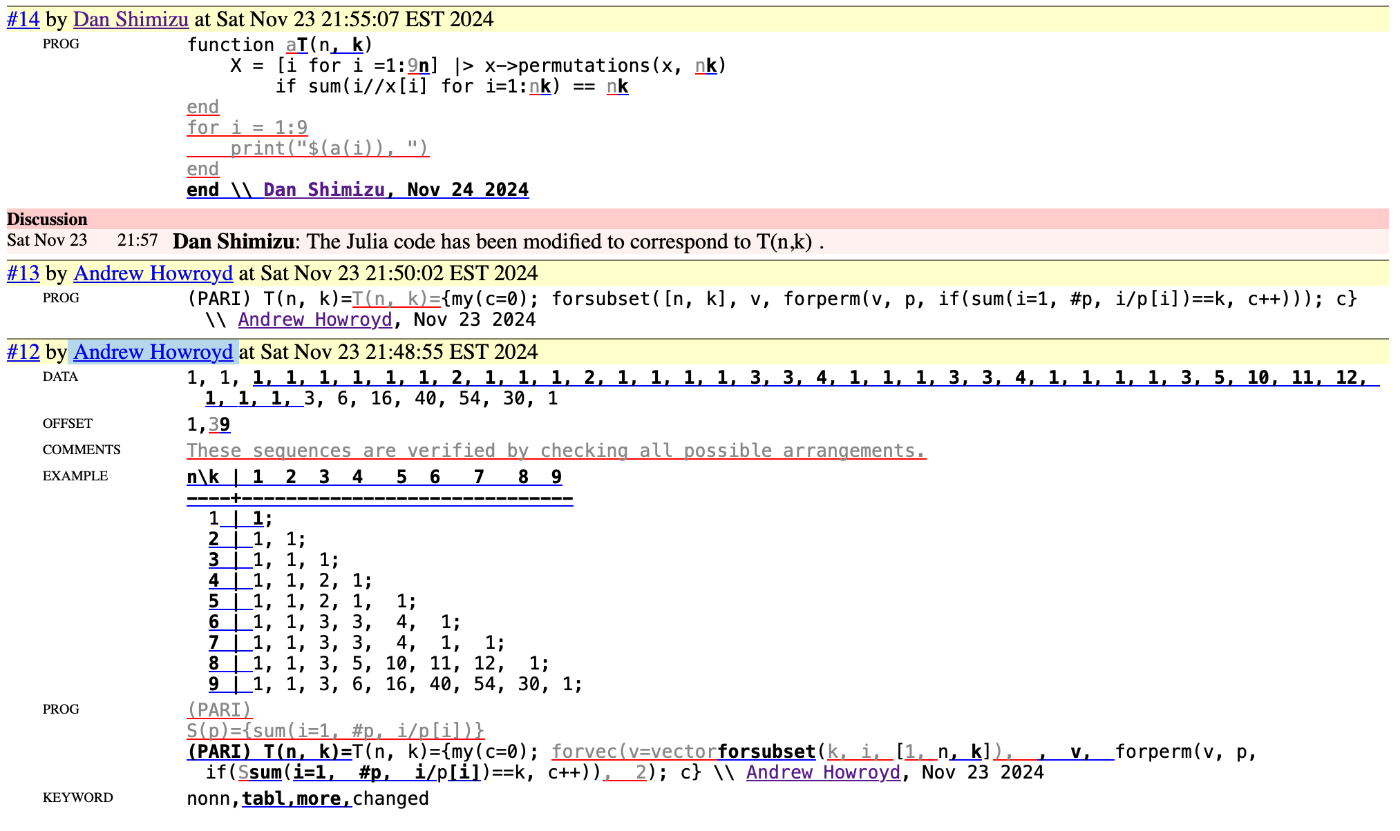
$n=10$から$13$ まで拡張する

今度はAlois P. Heinz さんが$T(n,k)$の$n＝10$から$13$のときのシーケンスを調べてくれました。
私のPC（M1のMacBookPro）では，$n=12$あたりから時間がかかっていて，$n=13$は試してません。

ついに承認！

管理者のN. J. A. Sloaneさんから承認の連絡が2024/12/3にありました。やった！

コードの追加

この後，Chai Wah Wu さんがpythonのコードを追加してくれました。

A378322

今回登録したシーケンスの番号はA378322です。

https://oeis.org/A378322

やりとりをざっくり紹介してきましたが，編集履歴はこちらからみることができます。

https://oeis.org/history?seq=A378322&start=0

まとめ

シーケンスは何が違っていたのか？

i/x[i]とi//x[i]でチェックしたのですが，ずれていたのは5つの順列でした。

using Combinatorics

X = [i for i =1:9] |> x->permutations(x,7)
Y = []
for x ∈ X
    if sum(i/x[i] for i=1:7) == 7
        push!(Y,x)
    end
end
Z = []
for x ∈ X
    if sum(i//x[i] for i=1:7) == 7
        push!(Z,x)
    end
end
set_Y = Set(Tuple.(Y))
set_Z = Set(Tuple.(Z))
difference = setdiff(set_Z, set_Y)

Set{NTuple{7, Int64}} with 5 elements:
(3, 1, 2, 8, 5, 9, 7)
(1, 4, 2, 8, 3, 9, 6)
(1, 2, 9, 8, 5, 3, 6)
(1, 3, 4, 2, 6, 8, 7)
(2, 1, 9, 8, 5, 4, 6)

和をとって，計算すると今回は無視できない誤差だったようです。

for x ∈ difference 
    println("有理数は$(sum(i//x[i] for i=1:7)),実数は$(sum(i/x[i] for i=1:7))")
end

有理数は7//1,実数は7.000000000000001
有理数は7//1,実数は7.000000000000001
有理数は7//1,実数は7.000000000000001
有理数は7//1,実数は6.999999999999999
有理数は7//1,実数は7.000000000000001

気づいたこと

Andrew Howroyd さんがテーブルを作ってくれました。（$n=9$まで）
$n=13$までテーブルを書いてみました。

T(n,k)	k = 1..n
T(1,k)	1;
T(2,k)	1, 1;
T(3,k)	1, 1, 1;
T(4,k)	1, 1, 2, 1;
T(5,k)	1, 1, 2, 1, 1;
T(6,k)	1, 1, 3, 3, 4, 1;
T(7,k)	1, 1, 3, 3, 4, 1, 1;
T(8,k)	1, 1, 3, 5, 10, 11, 12, 1;
T(9,k)	1, 1, 3, 6, 16, 40, 54, 30, 1;
T(10,k)	1, 1, 3, 7, 25, 88, 184, 206, 102, 1;
T(11,k)	1, 1, 3, 7, 25, 88, 184, 206, 102, 1, 1;
T(12,k)	1, 1, 3, 13, 56, 244, 744, 1329, 1623, 746, 749, 1;
T(13,k)	1, 1, 3, 13, 56, 244, 744, 1329, 1623, 746, 749, 1, 1;

$n$が1変化するときにあまり変化がない（末尾に1を加えるだけ）となっているのは

• $n=1$から$n=2$
• $n=2$から$n=3$
• $n=4$から$n=5$
• $n=6$から$n=7$
• $n=10$から$n=11$
• $n=12$から$n=13$

の時です。変化した後の$n$が素数のようですね。そうすると，オイラーのトーシェント関数あたりが関係しているかもしれませんね。

今後について

やっぱり，数学的に個数を考えたいですね。漸化式や生成関数（母関数）が見つかると最高です！