ユークリッドの互除法の拡張とJulia言語のgcdについて

はじめに

あけまして，おめでとうございます。2024年もよろしくお願いします。

私の勤務校で2学期に「整数」の分野を学習しました。その中で，「ユークリッドの互除法を文字式でも利用したい！」ということがあります。

連続する自然数は互いに素である。

証明は次のような形です。

【証明】
連続する自然数を$n$，$n+1$とする。

$$n+1=n\cdot 1+1$$

なので，ユークリッドの互助法を用いると，

$$(n+1,\,n)=(n,\,1)=1$$

よって，$n$ と $n+1$ は互いに素である。

このように文字を使ったユークリッドの互助法を用いるときに，「1以上の自然数に対して使う」 ことが暗黙の了解になっています。問題集の解答も，この辺りに抵触しないように書いてあることが多いように思います。（後述する「拡張した形」では見たことがありません。）

$(3n-5,\,1-3n)$の最大公約数などを考えたいので，まずは$0$や負の数のときのユークリッドの互除法を拡張します。そして，その性質をまとめ，問題を解いていこうと思います。

Julia言語での定義

まずは，Julia言語で最大公約数の関数gcdがどのように定義されているか調べます。

gcd関数

関数gcdを使うのに特別なパッケージは要りません。

最大公約数gcd(1)

gcd(100,10),gcd(257,32),gcd(78,1100)

(10, 1, 2)

0を含む場合

0含む場合です。

最大公約数gcd(2)

gcd(2,0),gcd(0,2),gcd(0,0)

(2, 2, 0)

0と0の最大公約数は0であることに注意してください。このことに関しては，以下 @FumiharuKato さんの𝕏のポストを参考にしてください。

https://twitter.com/FumiharuKato/status/1021420438981783553

負の数を含む場合

次に負の数を含む場合です。1以上の自然数が返されます。

最大公約数gcd(3)

gcd(-2,4),gcd(2,-4),gcd(-2,-4)

(2, 2, 2)

マニュアルをみると...

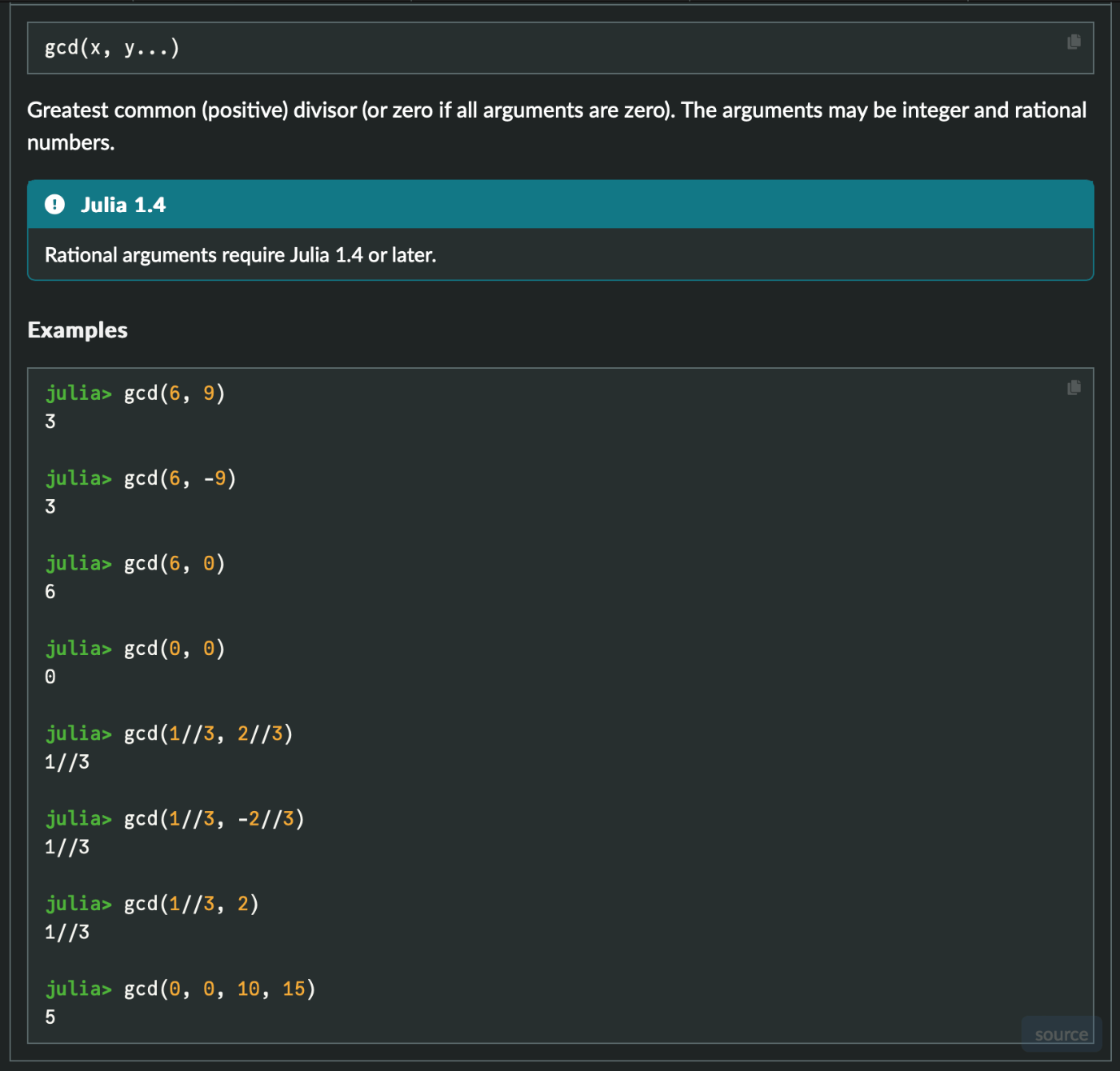
https://docs.julialang.org/en/v1/base/math/#Base.gcdを見ると，次のような例となっています。
有理数についても定義されていますね。

ユークリッドの互除法の再定義

再定義

まず，ユークリッドの互除法を整数全体で利用できるように，次のように再定義します。

https://www.math.titech.ac.jp/~hoya/Teaching/algebra2021sPDF/extEuc.pdfのサイトを参考にしました。

正の整数 $a$, $b\in\mathbb{Z}_{>0}$ に対して，その最大公約数を $(a, b)$ と書く. さらに $a$, $b\in\mathbb{Z}$に対する $(a, b)$ を 以下のように定義する :

• 任意の $0$ 以上の整数 $a\in\mathbb{Z}_{\leq 0}$ に対して $(0,a) = (a,0) = a$ とする。
• 各 $a$, $b\in\mathbb{Z}$ に対し，$(a, b) := (|a|, |b|)$ とする。

これで，0や負の数も考えることができます。

次の補題も確認しておきます。この補題により，$a=bq+r$の$q$や$r$は商，余りでなくても大丈夫です。

任意の $b,q,r\in\mathbb{Z}$ に対し，

$$(b,r)=(bq+r,b)$$

ユークリッドの互除法の性質

まずは，拡張前でも成り立つ性質です。

ユークリッドの互除法の性質(1）

$$(a,b)=(b,a)$$

ユークリッドの互除法の性質(2）
$n$を自然数とするとき

$$(na,nb)=n(a,b)$$

ユークリッドの互除法の性質(3）

$$(b,\,c)=1のとき，(a,b)=(ac,b)$$

3つ目の性質はあまり知られていませんが，式を変形するときに大切です。

0の導入

0が入る場合についてまとめておきます。

$$(x,\,0)=x\quad (x\in\mathbb{N})$$

$$(0,\,0)=0$$

負の数の導入

負の数が入る場合についてまとめておきます。

$$(a,\,b)=(-a,\,b)=(a,\,-b)=(-a,\,-b)$$

問題

具体的な問題とその答えとなります。

問題1

$n$を整数とする。$5n-2$と$3n+1$の最大公約数を求めよ。

【解答】

$$\begin{aligned} \bigstar&=(5n-2,\,3n+1)\\ &=(2n-3,\,3n+1)\cdots\cdots 5n-2=(3n+1)\times 1+2n-3\\ &=(2n-3,\,n+4)\cdots\cdots 3n+1=(2n-3)\times 1+n+4\\ &=(n-7,\,n+4)\cdots\cdots 2n-3=(n+4)\times 1+n-7\\ &=(n-7,\,11)\cdots\cdots n+4=(n-7)\times 1+11\\ \end{aligned}$$

$k\in \mathbb{Z}$として，

• $n=11k+7$のとき，$\bigstar=11$
• $n\ne 11k+7$のとき，$\bigstar=1$

コードで確認

function test(x,y)
    p = Int[]
    for n = x:y
        push!(p,gcd(5n-2,3n+1))
    end
    p
end

for i=0:10
println(test(i*10+1,i*10+10))
end

[1, 1, 1, 1, 1, 1, 11, 1, 1, 1]
[1, 1, 1, 1, 1, 1, 1, 11, 1, 1]
[1, 1, 1, 1, 1, 1, 1, 1, 11, 1]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 11]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
[11, 1, 1, 1, 1, 1, 1, 1, 1, 1]
[1, 11, 1, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 11, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 1, 11, 1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 11, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 1, 11, 1, 1, 1, 1]

問題2

$n$を整数とする。$n^5+5$と$n^3+3$の最大公約数を求めよ。

【解答】

$$\begin{aligned} \bigstar&=(n^5+5,\,n^3+3)\\ &=(n^3+3,-3n^2+5)\cdots\cdots n^5+5=(n^3+3)\times n^2-3n^2+5\\ &=(3(n^3+3),-3n^2+5)\cdots\cdots (3,-3n^2+5)=1\quad 性質(3)\\ &=(3n^3+9,-3n^2+5)\\ &=(-3n^2+5,5n+9)\cdots\cdots 3n^3+9=(-3n^2+5)\times(-n)+5n+9\\ &=(15n^2-25,5n+9)\cdots\cdots (5,5n+9)=1\quad 性質(3)\\ &=(5n+9,-27n-25)\cdots\cdots 15n^2-25=(5n+9)\times3n-27n-25\\ &=(27n+25,5n+9)\cdots\cdots 負の数の導入\\ &=(5n+9,2n-20)\cdots\cdots 27n+25=(5n+9)\times5+2n-20\\ &=(2n-20,n+49)\cdots\cdots 5n+9=(2n-20)\times2+n+49\\ &=(n+49,-118)\cdots\cdots 2n-20=(n+49)\times2-118\\ &=(n+49,118)\cdots\cdots 負の数の導入 \end{aligned}$$

$118=2\times59$（素因数分解）です。$k,m\in \mathbb{Z}$として，

• $n=118k-49$のとき，$\bigstar=118$
• $n=118k+10$のとき，$\bigstar=59$
• $n=2m-1 \wedge n\neq 118k-49$のとき，$\bigstar=2$
• 上記以外のとき，$\bigstar=1$

コードで確認

function test(x,y)
    p = Int[]
    for n = x:y
        push!(p,gcd(n^5+5,n^3+3))
    end
    p
end

for i=0:12
println(test(i*10+1,i*10+10))
end

[2, 1, 2, 1, 2, 1, 2, 1, 2, 59]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 118, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 1, 2, 1]
[2, 1, 2, 1, 2, 1, 2, 59, 2, 1]