Zenn
🦋

関数のグラフと最大値・最小値をJulia言語で考えてみる

に公開
Julia
高校数学
二次関数
idea

はじめに

高校1年生くらいに数学Iで「二次関数のグラフと最大値・最小値」について学びます。
生徒は「二次関数のグラフを描く」「最大・最小を求める」ことは頭で考えて，紙に書きます。
Julia言語などのコードを用いたときにどのような流れになるのを考えてみました。

問題

頭で考えて，紙に書く

実際に，頭で考えて，紙に書いてみました。（iPadのGoodnoteに書いているので紙ではないですね。。。）

(1) の手順は

  • 平方完成する
  • 頂点の位置，凹凸，y切片などを確認
  • グラフを描く

(2) の手順は

  • グラフより，最大値の位置を確認
  • 0\leqq x\leqq 3で考えて，最小値の位置を確認
  • 最大値・最小値を求める。

こんな感じでしょうか。

Julia言語で考えてみる

(1) グラフを描くときの基本は 「点を細かく取ってプロットする」 です。

xの値を0~3まで，0.01刻みで考え，そのときのf(x)=yの値を求めてテーブルを作ります。そして，その対応する点をプロットします。

# 関数定義
f(x) = -3x^2 + 6x - 1

# xの範囲を等間隔で作成
xs = 0:0.001:3
ys = f.(xs)

using Plots
scatter(xs,ys)

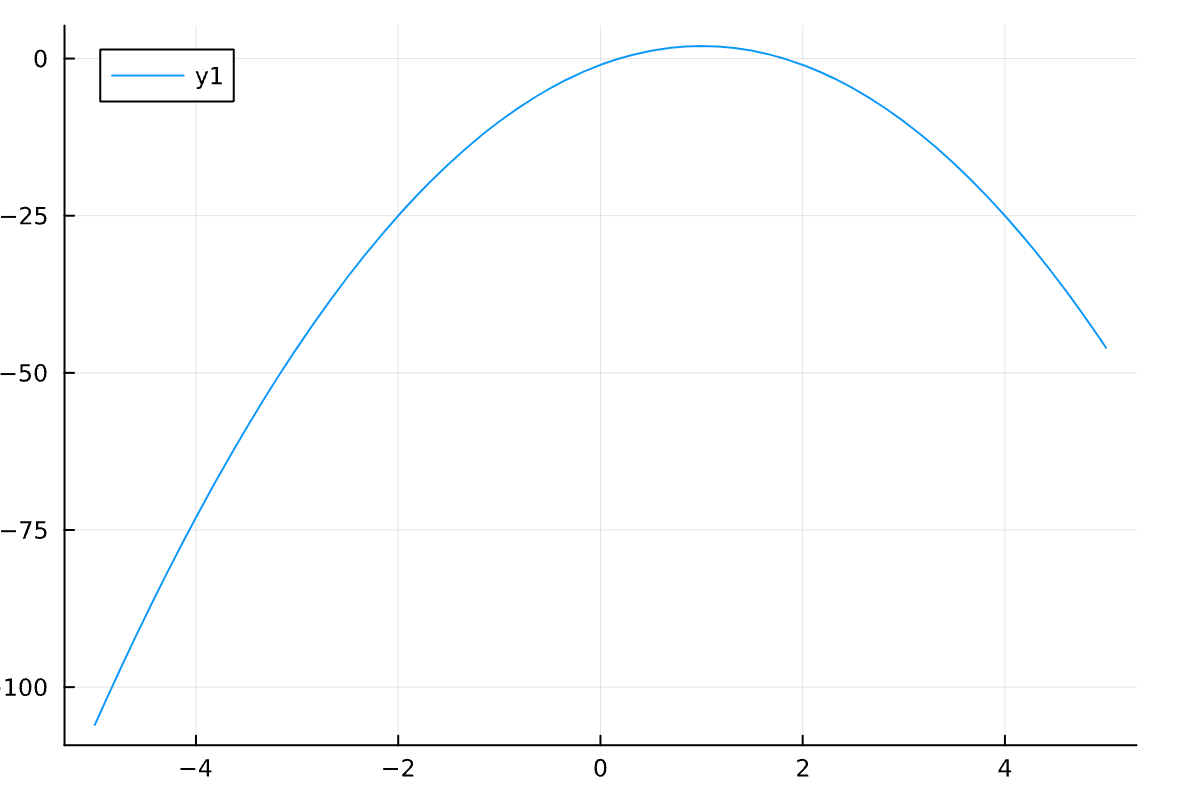
もちろん，簡単にグラフの概形を描くこともできます。

using Plots
f(x) = -3x^2 + 6x - 1
plot(f)

(2) 最大値・最小値は細かく刻んだ(x,y)の点を調べて，yの値が最大になるところ，最小になるところを調べれば求められます。

# 関数定義
f(x) = -3x^2 + 6x - 1

# xの範囲を等間隔で作成
xs = 0:0.001:3
ys = f.(xs)

# 最大値と最小値を求める
max_idx = argmax(ys)
min_idx = argmin(ys)

x_max = xs[max_idx]
y_max = ys[max_idx]

x_min = xs[min_idx]
y_min = ys[min_idx]


# 結果の表示
println("最大値: f($(x_max)) = $(y_max)")
println("最小値: f($(x_min)) = $(y_min)")

最大値: f(1.0) = 2.0
最小値: f(3.0) = -10.0

まとめ

Julia言語のコードを描いて求めた流れは，二次関数以外の一般的な関数でも利用できます。 頭で考えるとときには，二次関数のグラフの一般的な概形を知っておかなくてはならず，さらにその概形を考えるためには「平方完成」など頂点の情報が必須となります。

Julia言語での流れは，「グラフを描くとは？」「最大値・最小値を求めるとは？」というところにフォーカスしているようにも思えました。

せっかくですので，別の関数でもやってみます。

# 関数定義
f(x) = 2cos(x)-3sin(3x)

# xの範囲を等間隔で作成
xs = 0:0.001:3
ys = f.(xs)

# 最大値と最小値を求める
max_idx = argmax(ys)
min_idx = argmin(ys)

x_max = xs[max_idx]
y_max = ys[max_idx]

x_min = xs[min_idx]
y_min = ys[min_idx]


# 結果の表示
println("最大値: f($(x_max)) = $(y_max)")
println("最小値: f($(x_min)) = $(y_min)")

# グラフ
using Plots
plot(f,xlim=(0,3))

最大値: f(1.496) = 3.074243952525017
最小値: f(2.653) = -4.749460549591128

この関数の最大・最小を考えるためには，通常は「三角関数の微分」など理系の高校生がまなぶ数学IIIが必要で，結構大変ですね。頭で考えるにしても，一度，コードを利用して 「グラフの描画→最大値・最小値を求める」 の流れを見ておくのも大切なのではないでしょうか？

Discussion