Zenn
🦋

2025開成中の算数の問題について（長方形の分割）

2025/02/08に公開3件
Julia
math
tech

はじめに

2025年の受験シーズンですが，首都圏の中学入試はほぼ終わりました。私の勤務校でも無事入試を終えることができ（まだ高校入試はありますが．．．）ほっとしています。

他の中学校の入試問題もネットなどでみることができます。その中で，開成中の算数の長方形の分割の問題が目に留まりました。

やっぱり全パターン調べたいですよね。また，ポイントもあるので，どのような種類のポイントが作れるのかも気になるところです。

Julia言語

それでは今回もJulia言語でコードを作っていきましょう！

PCのスペックも記載しておきます。

長方形の配置について

長方形の配置の方針は面積の大きい長方形から順に配置することにしました。

  • 面積8→面積7→面積6→…→面積1

当初，全ての配置を検討して，重ならないケースをピックアップしようとしたのですが，実行に時間がかかったので，二つに分けることにしました。

その上，二つのケースを組み合わせて重ならないケースをピックアップしました。

面積8→面積7→面積6→面積5→面積4

面積8，面積6，面積4は複数の選択肢があります。

function generate_tile_combinations()
    tiles_8x1 = []
    for x = 1:2, y = 1:4
        push!(tiles_8x1, [(x+r-1, y+s-1) for r = 1:8, s = 1:1])
    end

    tiles_4x2 = []
    for x = 1:6, y = 1:3
        push!(tiles_4x2, [(x+r-1, y+s-1) for r = 1:4, s = 1:2])
    end

    tiles_2x4 = []
    for x = 1:8, y = 1:1
        push!(tiles_2x4, [(x+r-1, y+s-1) for r = 1:2, s = 1:4])
    end

    tiles_7x1 = []
    for x = 1:3, y = 1:4
        push!(tiles_7x1, [(x+r-1, y+s-1) for r = 1:7, s = 1:1])
    end

    tiles_6x1 = []
    for x = 1:4, y = 1:4
        push!(tiles_6x1, [(x+r-1, y+s-1) for r = 1:6, s = 1:1])
    end

    tiles_3x2 = []
    for x = 1:7, y = 1:3
        push!(tiles_3x2, [(x+r-1, y+s-1) for r = 1:3, s = 1:2])
    end

    tiles_2x3 = []
    for x = 1:8, y = 1:2
        push!(tiles_2x3, [(x+r-1, y+s-1) for r = 1:2, s = 1:3])
    end

    tiles_5x1 = []
    for x = 1:5, y = 1:4
        push!(tiles_5x1, [(x+r-1, y+s-1) for r = 1:5, s = 1:1])
    end

    tiles_4x1 = []
    for x = 1:6, y = 1:4
        push!(tiles_4x1, [(x+r-1, y+s-1) for r = 1:4, s = 1:1])
    end

    tiles_2x2 = []
    for x = 1:8, y = 1:3
        push!(tiles_2x2, [(x+r-1, y+s-1) for r = 1:2, s = 1:2])
    end

    tiles_1x4 = []
    for x = 1:9, y = 1:1
        push!(tiles_1x4, [(x+r-1, y+s-1) for r = 1:1, s = 1:4])
    end

    valid_combinations = []
    grid_positions = [(i, j) for i = 1:9, j = 1:4]

    for t8_set in [tiles_8x1, tiles_4x2, tiles_2x4], t8 in t8_set,
        t6_set in [tiles_6x1, tiles_3x2, tiles_2x3], t6 in t6_set,
        t4_set in [tiles_4x1, tiles_2x2, tiles_1x4], t4 in t4_set,
        t7 in tiles_7x1, t5 in tiles_5x1
            
            tile_set = union(t8, t7, t6, t5, t4)
            if length(tile_set) == 30
                push!(valid_combinations, tile_set)
            end
    end

    return valid_combinations
end

T = generate_tile_combinations()

13668-element Vector{Any}:
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4), (7, 4), (8, 4), (9, 4)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (7, 3), (8, 3), (7, 4), (8, 4)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (8, 2), (9, 2), (8, 3), (9, 3)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (8, 3), (9, 3), (8, 4), (9, 4)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (9, 1), (9, 2), (9, 3), (9, 4)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4), (7, 3), (8, 3), (7, 4), (8, 4)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4), (8, 2), (9, 2), (8, 3), (9, 3)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4), (8, 3), (9, 3), (8, 4), (9, 4)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4), (9, 1), (9, 2), (9, 3), (9, 4)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 3), (3, 4), (4, 4), (5, 4), (6, 4), (7, 4), (8, 2), (9, 2), (8, 3), (9, 3)]
 ⋮
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (7, 3), (1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (2, 3), (3, 3), (4, 3), (5, 3)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (7, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (1, 1), (2, 1), (3, 1), (4, 1)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (7, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (1, 2), (2, 2), (3, 2), (4, 2)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (7, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (2, 1), (3, 1), (4, 1), (5, 1)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (7, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (2, 2), (3, 2), (4, 2), (5, 2)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (7, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (1, 1), (2, 1), (1, 2), (2, 2)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (7, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (2, 1), (3, 1), (2, 2), (3, 2)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (7, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (3, 1), (4, 1), (3, 2), (4, 2)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (7, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (4, 1), (5, 1), (4, 2), (5, 2)]

13,668通りあります。コードの実行時間は30sほどです。

面積3→面積2→面積1

面積3，面積2，面積1の選択肢は以下の通りです。

function generate_small_tile_combinations()
    tiles_3x1 = []
    for x = 1:7, y = 1:4
        push!(tiles_3x1, [(x+r-1, y+s-1) for r = 1:3, s = 1:1])
    end

    tiles_1x3 = []
    for x = 1:9, y = 1:2
        push!(tiles_1x3, [(x+r-1, y+s-1) for r = 1:1, s = 1:3])
    end

    tiles_2x1 = []
    for x = 1:8, y = 1:4
        push!(tiles_2x1, [(x+r-1, y+s-1) for r = 1:2, s = 1:1])
    end

    tiles_1x2 = []
    for x = 1:9, y = 1:3
        push!(tiles_1x2, [(x+r-1, y+s-1) for r = 1:1, s = 1:2])
    end

    tiles_1x1 = []
    for x = 1:9, y = 1:4
        push!(tiles_1x1, [(x, y)])
    end

    
    valid_small_combinations = []
    grid_positions = [(i, j) for i = 1:9, j = 1:4]

    for t3_set in [tiles_3x1, tiles_1x3], t3 in t3_set,
        t2_set in [tiles_2x1, tiles_1x2], t2 in t2_set,
        t1 in tiles_1x1
            
            tile_set = union(t3, t2, t1)
            if length(tile_set) == 6
                push!(valid_small_combinations, tile_set)
            end
    end

    return valid_small_combinations
end

U = generate_small_tile_combinations()


72354-element Vector{Any}:
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (1, 3)]
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (1, 4)]
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (2, 3)]
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (2, 4)]
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (3, 2)]
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (3, 3)]
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (3, 4)]
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (4, 1)]
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (4, 2)]
 [(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (4, 3)]
 ⋮
 [(9, 2), (9, 3), (9, 4), (8, 3), (8, 4), (6, 3)]
 [(9, 2), (9, 3), (9, 4), (8, 3), (8, 4), (6, 4)]
 [(9, 2), (9, 3), (9, 4), (8, 3), (8, 4), (7, 1)]
 [(9, 2), (9, 3), (9, 4), (8, 3), (8, 4), (7, 2)]
 [(9, 2), (9, 3), (9, 4), (8, 3), (8, 4), (7, 3)]
 [(9, 2), (9, 3), (9, 4), (8, 3), (8, 4), (7, 4)]
 [(9, 2), (9, 3), (9, 4), (8, 3), (8, 4), (8, 1)]
 [(9, 2), (9, 3), (9, 4), (8, 3), (8, 4), (8, 2)]
 [(9, 2), (9, 3), (9, 4), (8, 3), (8, 4), (9, 1)]

72,354通りあります。コードの実行時間は0.5sほどです。

二つを組み合わせてチェックする

2つを組み合わせ，チェックしますが，これはちょっと時間がかかりました。下記のコードで13minほどかかっています。結局どのように「二つに分けるのがいいかな？」というときに，上記の二つの分け方が良さそうでした。（というよりも，他の分け方はクルクルして実行時間が長そうでした。）

function combine_solutions(big_sets, small_sets, target_size=36)
    results = []
    for big in big_sets, small in small_sets
        union_set = union(big, small)
        if length(union_set) == target_size
            push!(results, union_set)
        end
    end
    return results
end

V = combine_solutions(T, U)

10344-element Vector{Any}:
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 4), (7, 4), (8, 4), (9, 4), (7, 3), (8, 3), (9, 3), (8, 2), (9, 2), (9, 1)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 4), (7, 4), (8, 4), (9, 4), (7, 3), (8, 3), (9, 3), (9, 1), (9, 2), (8, 2)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 4), (7, 4), (8, 4), (9, 4), (9, 1), (9, 2), (9, 3), (7, 3), (8, 3), (8, 2)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (6, 4), (7, 4), (8, 4), (9, 4), (9, 1), (9, 2), (9, 3), (8, 2), (8, 3), (7, 3)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (9, 1), (9, 2), (9, 3), (9, 4), (6, 4), (7, 4), (8, 4), (7, 3), (8, 3), (8, 2)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (9, 1), (9, 2), (9, 3), (9, 4), (6, 4), (7, 4), (8, 4), (8, 2), (8, 3), (7, 3)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (9, 1), (9, 2), (9, 3), (9, 4), (8, 2), (8, 3), (8, 4), (6, 4), (7, 4), (7, 3)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (9, 1), (9, 2), (9, 3), (9, 4), (8, 2), (8, 3), (8, 4), (7, 3), (7, 4), (6, 4)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (9, 1), (9, 2), (9, 3), (9, 4), (8, 2), (8, 3), (8, 4), (7, 3), (7, 4), (1, 4)]
 [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (7, 1), (8, 1), (1, 2), (2, 2)  …  (9, 1), (9, 2), (9, 3), (9, 4), (8, 2), (8, 3), (8, 4), (1, 4), (2, 4), (7, 3)]
 ⋮
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (2, 2), (3, 2), (4, 2), (5, 2), (3, 1), (4, 1), (5, 1), (1, 1), (1, 2), (2, 1)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (1, 1), (2, 1), (1, 2), (2, 2), (3, 1), (4, 1), (5, 1), (3, 2), (4, 2), (5, 2)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (1, 1), (2, 1), (1, 2), (2, 2), (3, 1), (4, 1), (5, 1), (4, 2), (5, 2), (3, 2)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (1, 1), (2, 1), (1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (3, 1), (4, 1), (5, 1)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (1, 1), (2, 1), (1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (4, 1), (5, 1), (3, 1)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (4, 1), (5, 1), (4, 2), (5, 2), (1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (3, 2)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (4, 1), (5, 1), (4, 2), (5, 2), (1, 1), (2, 1), (3, 1), (2, 2), (3, 2), (1, 2)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (4, 1), (5, 1), (4, 2), (5, 2), (1, 2), (2, 2), (3, 2), (1, 1), (2, 1), (3, 1)]
 [(8, 1), (9, 1), (8, 2), (9, 2), (8, 3), (9, 3), (8, 4), (9, 4), (1, 4), (2, 4)  …  (4, 1), (5, 1), (4, 2), (5, 2), (1, 2), (2, 2), (3, 2), (2, 1), (3, 1), (1, 1)]

10,344通りとなりました。次はポイントです。

ポイントの計算

この後，図示もするのですが，y座標は下から上となります。なので，ポイントを計算するときに一度ひっくり返しました。そして，今回の計算はy座標の取りうる値を加えていけばいいことがわかります。

function calculate_score(values)
    score = 0
    for value in values
        if value == 1
            score += 4
        elseif value == 2
            score += 3
        elseif value == 3
            score += 2
        elseif value == 4
            score += 1
        end
    end
    return score
end

function compute_max_score(solutions)
    scores = []
    for solution in solutions
        score_a = calculate_score(union([coord[2] for coord in solution[1:8]]))
        score_b = calculate_score(union([coord[2] for coord in solution[9:15]]))
        score_c = calculate_score(union([coord[2] for coord in solution[16:21]]))
        score_d = calculate_score(union([coord[2] for coord in solution[22:26]]))
        score_e = calculate_score(union([coord[2] for coord in solution[27:30]]))
        score_f = calculate_score(union([coord[2] for coord in solution[31:33]]))
        score_g = calculate_score(union([coord[2] for coord in solution[34:35]]))
        score_h = calculate_score(union([coord[2] for coord in solution[36:36]]))
        push!(scores, score_a + score_b + score_c + score_d + score_e + score_f + score_g + score_h)
    end
    return scores
end

compute_max_score(V) |> findmax,compute_max_score(V) |> findmin


((46, 3783), (20, 1))

最大のポイントは46点，最小のポイントは20点であることがわかりました。

長方形の配置の図示

それでは長方形の配置を図示してみましょう。まず，図示する関数を作ります。


using Plots

function draw_rectangle(x, y, width, height)
    rectangle = Shape([x, x + width, x + width, x], [y, y, y + height, y + height])
    plot!(rectangle, color=:white, linecolor=:black, aspectratio=true, label=false)
    annotate!(x + width / 2, y + height / 2, text(string(width * height), :black, :center))
end

function draw_diagram(coordinates)
    plot(grid=false, axis=false)
    for i in 1:8
        index = 36 - (((9 - i + 1)^2 - (9 - i + 1)) // 2) + 1 |> Int
        index_2 = index + 8 - i
        width_2 = coordinates[index_2][1] - coordinates[index][1] +1
        height_2 = coordinates[index_2][2] - coordinates[index][2] +1
        draw_rectangle(coordinates[index][1], coordinates[index][2], width_2,height_2)
    end
    plot!()
end

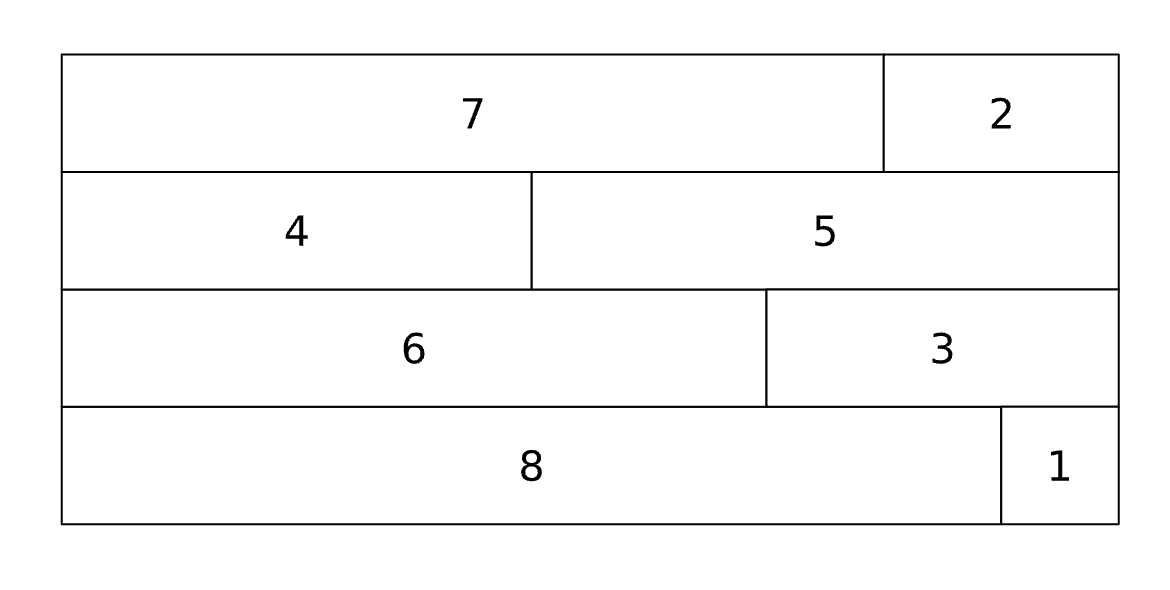
ポイント最大のポイント46点の場合を表示してみます。これは46点の場合の一例となります。

draw_diagram(V[3783])

次に，ポイント最小のポイント20点の場合を表示してみます。これも一例となります。

draw_diagram(V[1])

まとめ

全部調べると，いろいろ気になります。

せっかくなので，調べてみました。

ポイントと長方形の配置数について

for i =20:46
    k = findall(x -> x == i,compute_max_score(V)) |>length
    println("ポイントが$i 点となるのは$k 通り")
end

ポイントが20 点となるのは384 通り
ポイントが21 点となるのは96 通り
ポイントが22 点となるのは192 通り
ポイントが23 点となるのは280 通り
ポイントが24 点となるのは400 通り
ポイントが25 点となるのは416 通り
ポイントが26 点となるのは652 通り
ポイントが27 点となるのは786 通り
ポイントが28 点となるのは1010 通り
ポイントが29 点となるのは860 通り
ポイントが30 点となるのは640 通り
ポイントが31 点となるのは678 通り
ポイントが32 点となるのは668 通り
ポイントが33 点となるのは354 通り
ポイントが34 点となるのは378 通り
ポイントが35 点となるのは512 通り
ポイントが36 点となるのは468 通り
ポイントが37 点となるのは372 通り
ポイントが38 点となるのは298 通り
ポイントが39 点となるのは356 通り
ポイントが40 点となるのは64 通り
ポイントが41 点となるのは128 通り
ポイントが42 点となるのは4 通り
ポイントが43 点となるのは80 通り
ポイントが44 点となるのは108 通り
ポイントが45 点となるのは80 通り
ポイントが46 点となるのは80 通り

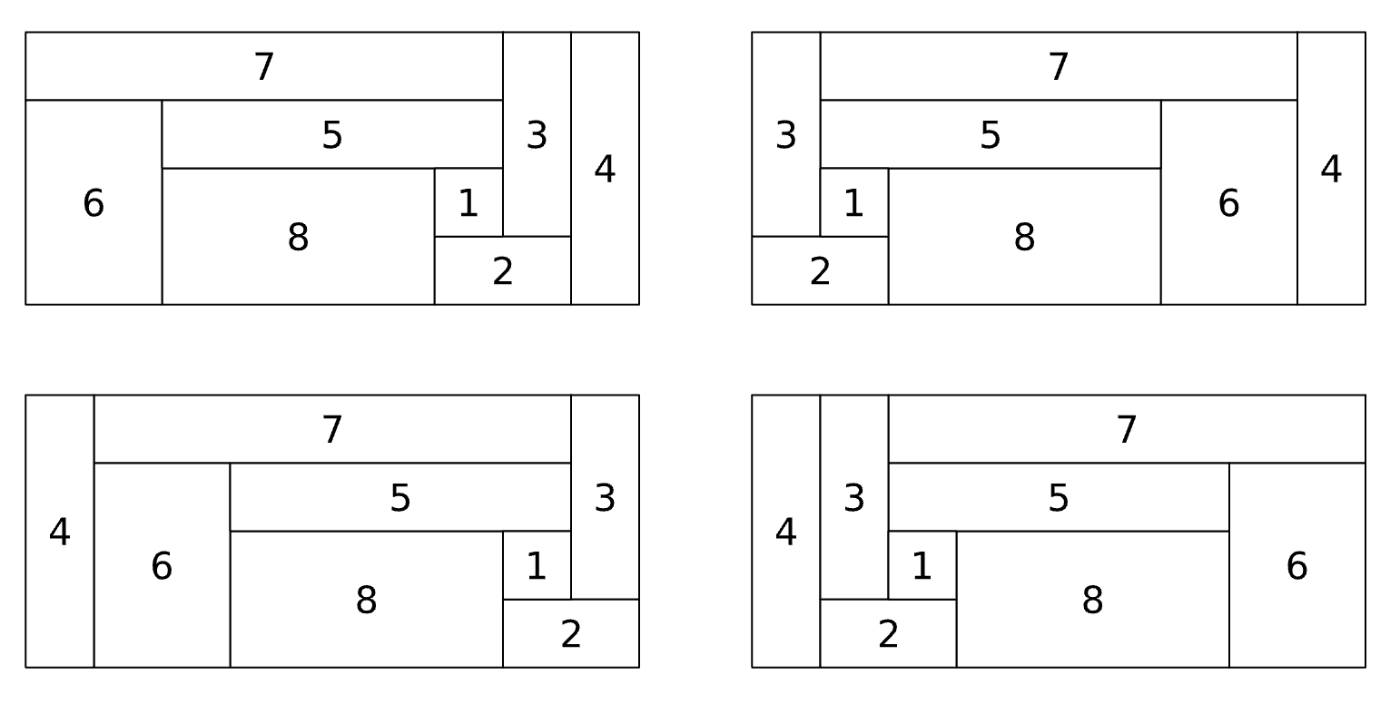
なるほど。ポイント42点が鬼門のように見えますね。

ポイント42点

list = findall(x -> x == 42, compute_max_score(V))
plots = []
for  i in list
    push!(plots,  draw_diagram(V[i]))
end
plot(plots...,size=(800,400))

ギャラリー

最後に，ポイント20〜46の一例をギャラリーにします。

function generate_plots(solutions, scores, score_range=20:46, grid_size=(6, 5), plot_size=(1500, 1500), filename="plot1.png")
    plots = []
    for score in score_range
        index = findfirst(x -> x == score, scores)
        draw_diagram(solutions[index])
        push!(plots, plot!(title=string(score)))
    end
    plot(plots..., size=plot_size, layout=grid_size)
    savefig(filename)
end

generate_plots(V,compute_max_score(V))

Discussion

さざんかぬふさざんかぬふ

おもしろいですね。全体の左上から順番に長方形をあてはめていく方針でpythonで全列挙してみたら、同じ答えが出ました。
手順にすると意外とステップ数が多くなり、中学受験の問題でも複雑なことをやっているのですね。
実行に数秒かかります。

from collections import defaultdict
# from pprint import pprint


width = 9
height = 4
board = [[0] * width for _ in range(height)]
used_rectangle = [0] * 9
rectangle_count = 0
score_count = defaultdict(int)


def search_empty_position():
    for i in range(height):
        for j in range(width):
            if board[i][j] == 0:
                return i, j


def is_paintable(top, left, rectangle_height, rectangle_width):
    for i in range(top, top + rectangle_height):
        for j in range(left, left + rectangle_width):
            if board[i][j]:
                return False
    return True


def paint(top, left, rectangle_height, rectangle_width, color):
    for i in range(top, top + rectangle_height):
        for j in range(left, left + rectangle_width):
            board[i][j] = color


def calculate_score():
    score = 0
    for i in range(height):
        score += (i + 1) * len(set(board[i]))
    return score


def calculate_all():
    global rectangle_count
    top, left = search_empty_position() or (-1, -1)
    if top == -1:
        score = calculate_score()
        # print('-' * 20)
        # print(score)
        # pprint(board)
        score_count[score] += 1
        return
    rectangle_count += 1
    for rectangle_height in range(1, height - top + 1):
        for rectangle_width in range(1, width - left + 1):
            rectangle_area = rectangle_height * rectangle_width
            if rectangle_area <= 8 and used_rectangle[rectangle_area] == 0 and is_paintable(
                    top, left, rectangle_height, rectangle_width):
                used_rectangle[rectangle_area] = rectangle_count
                paint(top, left, rectangle_height, rectangle_width, rectangle_count)
                calculate_all()
                # 後始末
                paint(top, left, rectangle_height, rectangle_width, 0)
                used_rectangle[rectangle_area] = 0
    rectangle_count -= 1


calculate_all()
# print({k: score_count[k] for k in sorted(score_count)})
for k in sorted(score_count):
    print(f'ポイントが{k} 点となるのは{score_count[k]} 通り')
清水団清水団

ありがとうございます！
こちらの方針の方が速そうですね。

清水団清水団

Python のコードをJuliaに移植しました。
実行時間0.4sでした。方針大事ですね。

using Base.Iterators

const width = 9
const height = 4
board = zeros(Int, height, width)
used_rectangle = zeros(Int, 9)
rectangle_count = Ref(0)
score_count = Dict{Int, Int}()

function search_empty_position()
    for i in 1:height, j in 1:width
        if board[i, j] == 0
            return i, j
        end
    end
    return -1, -1
end

function is_paintable(top, left, rectangle_height, rectangle_width)
    for i in top:(top + rectangle_height - 1), j in left:(left + rectangle_width - 1)
        if board[i, j] != 0
            return false
        end
    end
    return true
end

function paint(top, left, rectangle_height, rectangle_width, color)
    for i in top:(top + rectangle_height - 1), j in left:(left + rectangle_width - 1)
        board[i, j] = color
    end
end

function calculate_score()
    score = 0
    for i in 1:height
        score += i * length(unique(board[i, :]))
    end
    return score
end

function calculate_all()
    top, left = search_empty_position()
    if top == -1
        score = calculate_score()
        score_count[score] = get(score_count, score, 0) + 1
        return
    end
    
    rectangle_count[] += 1
    for rectangle_height in 1:(height - top + 1), rectangle_width in 1:(width - left + 1)
        rectangle_area = rectangle_height * rectangle_width
        if rectangle_area <= 8 && used_rectangle[rectangle_area] == 0 && is_paintable(top, left, rectangle_height, rectangle_width)
            used_rectangle[rectangle_area] = rectangle_count[]
            paint(top, left, rectangle_height, rectangle_width, rectangle_count[])
            calculate_all()
            # 後始末
            paint(top, left, rectangle_height, rectangle_width, 0)
            used_rectangle[rectangle_area] = 0
        end
    end
    rectangle_count[] -= 1
end

calculate_all()
for k in sort(collect(keys(score_count)))
    println("ポイントが ", k, " 点となるのは ", score_count[k], " 通り")
end


ポイントが 20 点となるのは 384 通り
ポイントが 21 点となるのは 96 通り
ポイントが 22 点となるのは 192 通り
ポイントが 23 点となるのは 280 通り
ポイントが 24 点となるのは 400 通り
ポイントが 25 点となるのは 416 通り
ポイントが 26 点となるのは 652 通り
ポイントが 27 点となるのは 786 通り
ポイントが 28 点となるのは 1010 通り
ポイントが 29 点となるのは 860 通り
ポイントが 30 点となるのは 640 通り
ポイントが 31 点となるのは 678 通り
ポイントが 32 点となるのは 668 通り
ポイントが 33 点となるのは 354 通り
ポイントが 34 点となるのは 378 通り
ポイントが 35 点となるのは 512 通り
ポイントが 36 点となるのは 468 通り
ポイントが 37 点となるのは 372 通り
ポイントが 38 点となるのは 298 通り
ポイントが 39 点となるのは 356 通り
ポイントが 40 点となるのは 64 通り
ポイントが 41 点となるのは 128 通り
ポイントが 42 点となるのは 4 通り
ポイントが 43 点となるのは 80 通り
ポイントが 44 点となるのは 108 通り
ポイントが 45 点となるのは 80 通り
ポイントが 46 点となるのは 80 通り