👋

高校数学の「データの分析」を JuliaとPluto.jlでWeb上に公開してみた

2023/01/01に公開

GitHub

Julia

math

idea

はじめに

現在，中学3年生の数学を担当して教えていますが，3学期から「データの分析」を学習します。この分野は比較的新しく，高校数学に入ってきた内容です。最新のカリキュラムでは「外れ値」「仮説検定の考え方」などが加わりました。

授業では，教科書を見ながら，教科書の「練習」という問題をみんなで解く形で進めています。まあ，せっかくなので，「手計算だけではなく，Juliaを使って計算してみたい！」と思いました。

＜使っている教科書＞

やってみると，色々な発見があったので，まとめることにしました。

Julia + Pluto.jl

実際，どうのようにまとめようか考えました。ポイントは

生徒が見ることができて，ちょっと変更したり実験できるようにする。
Pythonは使いたくない。。。（個人的な意見です）
Excelは使いたくない。。。（これも個人的な意見です）
Juliaを使いたい。。。（これも個人的な意見です）

とうことで，juliaを使うわけですが，「生徒が見ることができて，ちょっと変更したり実験できるようにする。」ことをどう実現するか考えました。

東京大学の松井さん（@utokyo_bunny）のところでもjuliaとcodespaceを使って線形代数のカリキュラムを作っているので，いいなあと年末に思っていたのですが，codespaceでvscode風なフロントエンドはちょっと敷居が高いかな。。。と思っていました。

ごまふあざらしさん（@MathSorcerer）の年末のjuliaのアドベントカレンダーを見ていたら，Plutoでwebサイトが作られていたので，こんな感じがいいなーと思ってました。また，Plutoでhtmlに書き出して作ると，binderと連携して，Juliaをローカルにインストールしなくても実行できることもわかりました。

サイトの左上のEdit or run this notobookをクリックして，binderにするか，ダウンロードして，julia+Plito.jlを使うか選びます。

binderはweb上で動かせますが，5分くらい読み込みに時間がかかり，実行も10分以上かかると再接続みたいです。でも，お手軽に体験できるのでよしとします。

これでやってみたいと思います。

作ったサイトの紹介

先に，作ったサイトを見てもらうのが早そうです。

作りながら思ったこと

ここからは項目に沿って，その時感じたことをメモします。

データの整理

最初は「データをインタラクティブに切り替えながらできると面白い！」と思って色々やっていたのですが，キリがないのでやめました。（別の機会に。。。）

データを階級に分けて，ヒストグラムにしました。

data1

data1=[
8.3
13.0
8.4
7.9
7.0
3.7
6.1
8.5
8.6
11.9
12.1
14.4
7.0
10.5
6.6
10.6
16.6
19.1
20.1
19.8
24.5
12.6
16.4
13.0
13.3
14.1
14.4
17.0
21.3
24.5]

階級

md"""
__度数分布表__


階級（℃） | 度数（日）
:------------ | :-------------:
3以上6未満 | $(count(i->(3<=i<6),data1))
6〜9 | $(count(i->(6<=i<9),data1))
9〜12 | $(count(i->(9<=i<12),data1))
12〜15 | $(count(i->(12<=i<15),data1))
15〜18 | $(count(i->(15<=i<18),data1))
18〜21 | $(count(i->(18<=i<21),data1))
21〜24 | $(count(i->(21<=i<24),data1))
24〜27 | $(count(i->(24<=i<27),data1))
27〜30 | $(count(i->(27<=i<30),data1))

"""

ヒストグラム


using StatsPlots　#グラフを作成
ENV["GKS_ENCODING"] = "utf8"　
	gr(fontfamily="IPAMincho") #グラフのタイトルを日本語化

histogram(data1,bin=3:3:30,title="最高気温（2018年4月）",label="札幌　",ygrid=true,xgrid=true,xticks=0:3:36,yticks=0:1:20)

データの代表値

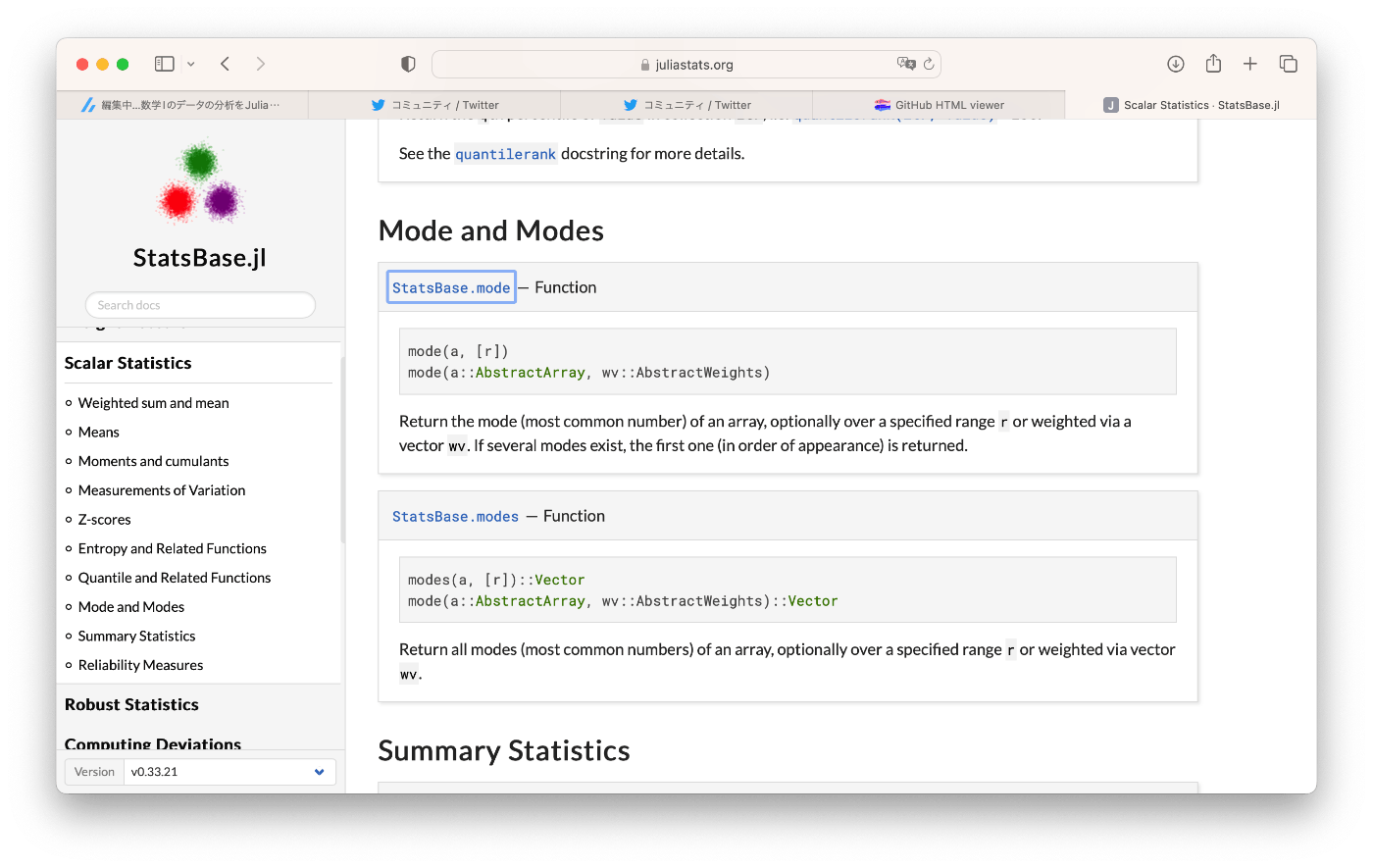
パッケージはStatsBase.jlを使いました。

平均値はmean，中央値はmedian，最頻値はStatsBase.modeです。

それぞれ関数を使っても良かったのですが，授業なのでcodeを書いてみました。

平均値

function heikin(x)
	S = 0
	for i=1:length(x)
		S +=x[i]
	end
	heikin = S/length(x)
end

中央値

function chuo(x)
	p = sort(x)
	n = length(p)
	if n % 2 == 0
		(p[n ÷ 2]  + p[n ÷ 2 +1] )/2
	else p[(n+1) ÷ 2] /1
	end
end

最頻値

function saihin(y,k)# kは階級の幅
	data = map(x->floor(x/k)*k+k/2, y)
	data2 = union(data)
	A = []
	for i in data2
	 	push!(A,count(a->(a==i),data))
	end
	data2[findmax(A)[2]]
end

最頻値は難しい

書いて分かったことは，最頻値難しいです。特に最頻値は「一意ではない」ということです。

説明を見ると，「最初に出てきた1つをにするよ。」と書いてあったので，「そんなものか。」と思いました。（どの階級にするか指定する方法もありました。）

データの散らばりと四分位範囲

まずは，木村さん（@kimu3_slime）のページを参考にさせてもらいました.

https://math-fun.net/20220228/22516/

箱ひげ図はboxplotで実現できるようですね。そして，四分位数もquantileを使えば良さそうだったのですが，これは大変でした。

四分位数の定義について

簡単に言うと，高校数学で用いる四分位数の定義とjuliaに実装されている定義が違います。「オプションで何かしてすればいいのか？」と軽く考えていたのですが，ちょっとわかりませんでした。

黒木さん（@genkuroki）が作成したものを利用しました。

四分位数

# 文部科学省による高校数学での四分位数の定義。
# 定義をこれだけに限定する問題はやめてほしい！
# https://twitter.com/genkuroki/status/1220149411818307584
function quantiles_monka(X) 
	X =  sort(X)
	n = length(X)
	k = iseven(n) ? 1 : 2
	Float64[
		X[1],
		median(@view X[1:(n ÷ 2)]),
		median(X),
		median(@view X[(n ÷ 2 + k):end]),
		X[end]
	]
end

奥村さん（@h_okumura）の四分位数の定義について詳しく説明していただいたHPも参考にしました。

箱ひげ図はboxplotを使ってい感じです。外れ値も表示されるみたいですね。

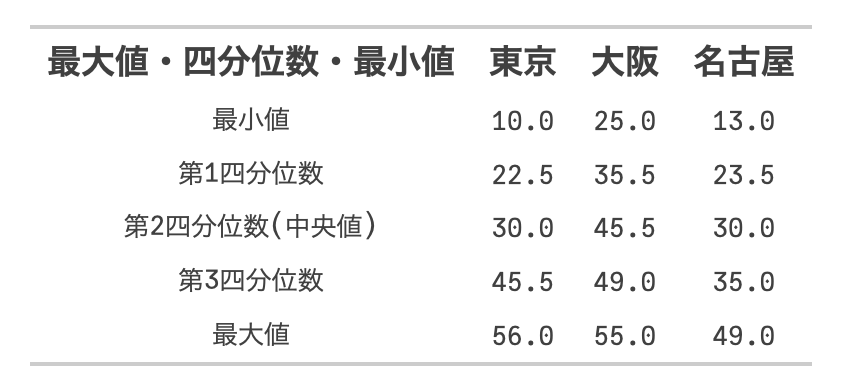
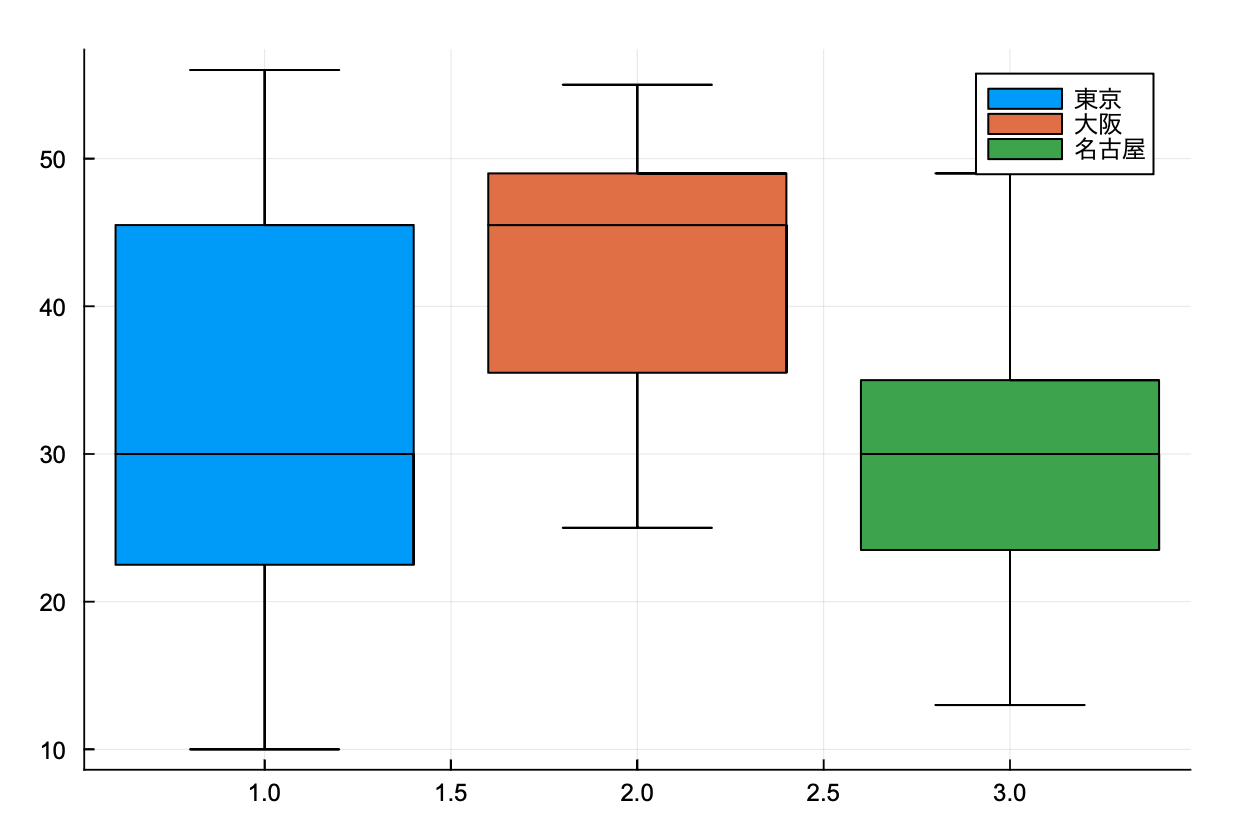
分散と標準偏差

まず，「不偏」出ないことを確認することはわかっていたので，そこは気をつけました。パッケージはStatistics.jlを利用しました。

分散はvar(data, corrected=false)
標準偏差はstd(data, corrected=false)

これも，codeを書いてみました。

分散

function bunsan(x)
	μ = mean(x)
	n = length(x)
	v = 0
	for i =1:n
		v += (x[i]-μ)^2/n
	end
	v
end

標準偏差はルート取るだけなので省略。教科書には変数の変換の問題もあった。

2つの変量の間の関係

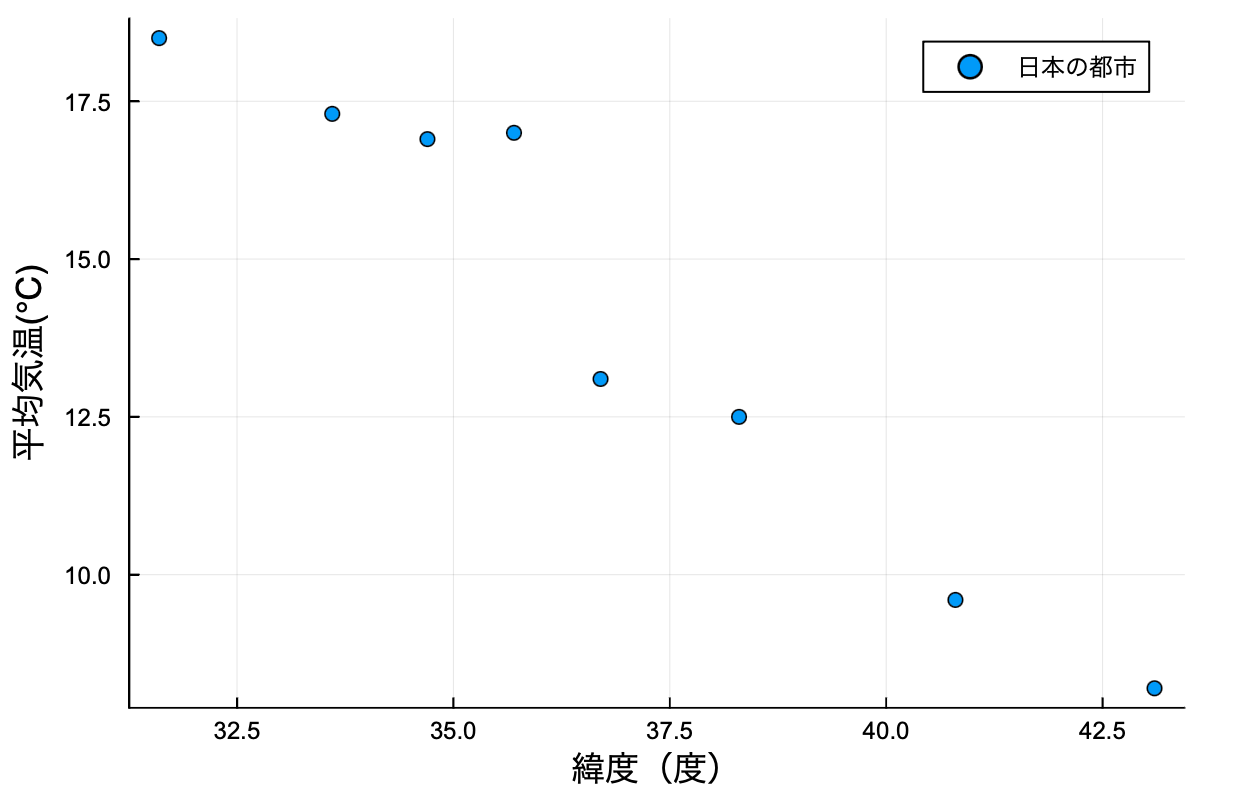
まずは散布図。scatterを使いました。

散布図

x = [43.1,40.8,38.3,35.7,36.7,34.7,33.6,31.6]

y = [8.2,9.6,12.5,17.0,13.1,16.9,17.3,18.5]

scatter(x,y,xlabel="緯度（度）",ylabel="平均気温(℃)",label="日本の都市　　　　")

共分散cov(testA,testB,corrected=false)
相関係数cor(testA,testB)

共分散

function kyobunsan(x,y)
	n = length(x)
	a = 0
	μ_x = mean(x)
	μ_y = mean(y)
	for i = 1:n
		a += (x[i]-μ_x)*(y[i]-μ_y)
	end
	a/n
end

相関係数

function soukan(x,y)
	kyobunsan(x,y)/(std(x,corrected=false)*std(x,corrected=false))
end

仮設検定の考え方

ここは新しい内容です。どのような問題か紹介します。

問題1つ目

仮説検定その1

function kentei(x,l,m)
	kakuritu = 0
	for i=l:m
		kakuritu += x[i]/200
	end
	println("確率は$(kakuritu) である")
	if kakuritu < 0.05
		println("水道水がおいしくなったと判断できる。")
	else println("水道水がおいしくなったと判断できない。")
	end
end

問題2つ目

仮説検定その2

function kentei2(k,n)
	kakuritu = 0
	for i=k:n
		kakuritu += binomial(n,i)*.5^i
	end
	println("確率は$(kakuritu) である")
	if kakuritu < 0.05
		println("このコインは出やすいと判断できる。")
	else println("このコインは出やすいと判断できない。")
	end
end

現在の高校数学のデータの分析における仮説検定の問題を解いて感じたことは，

片側検定である。（普通は両側検定ではないのか？）特にp値として0.05が出てきているが，これは両側検定でよく使われるp値ではないだろうか？だとすると，0.025くらいにしたほうがいいとも思える。
モデルとする分布を実験して具体的に与えられるが，どちら側を使えばいいのかわかりにくい。（どちらを使ってもいいと思われるが，具体的に実験で与えられた分布だと，答えが変化する可能性がある。）
二項分布をモデルとして与えられる場合がある。

まとめ

データの分析は，共通テストにも出題される分野で，多くの生徒が学習します。手計算で求めることも要求されますが，

多くのデータについて調べてみる。
データを変化させるとどうなるかを観察する。

このような実験を経験することは大切だと思います。「ちょっとこの数字を変えてみると...」と使ってもらえるといいです。