Juliaでブートストラップ法の推定を行う
Julia Advent Calendar 2024(シリーズ2)の16日目です。
はじめに
Xのポストで@HirokazuOHSAWAさんから次のような投稿がありました。
問題
問題をもう一度見てみます。
答え
正規分布の再生性の問題です。
-
X Y -
X\sim N(50,10^2) Y\sim N(50,10^2)
なので,A方式の方が合格の可能性が高いと言えます。
juliaのコード
Juliaのコードを見てみましょう。
using Distributions
X = Normal (50,10) ;
Y = Normal (50,10) ;
A = 2X
Normal{Float64} (μ=100.0, σ=20.0)
B = convolve(X,Y)
Normal{Float64} (μ=100.0, σ=14.142135623730951))
ccdf(A,120) , ccdf(B,120)
(0.15865525393145702, 0.07864960352514257)
確かに,Aの確率の方が大きいですね。
using StatsPlots , Distributions
plot(A,label="2X")
plot!(B,label="X+Y")
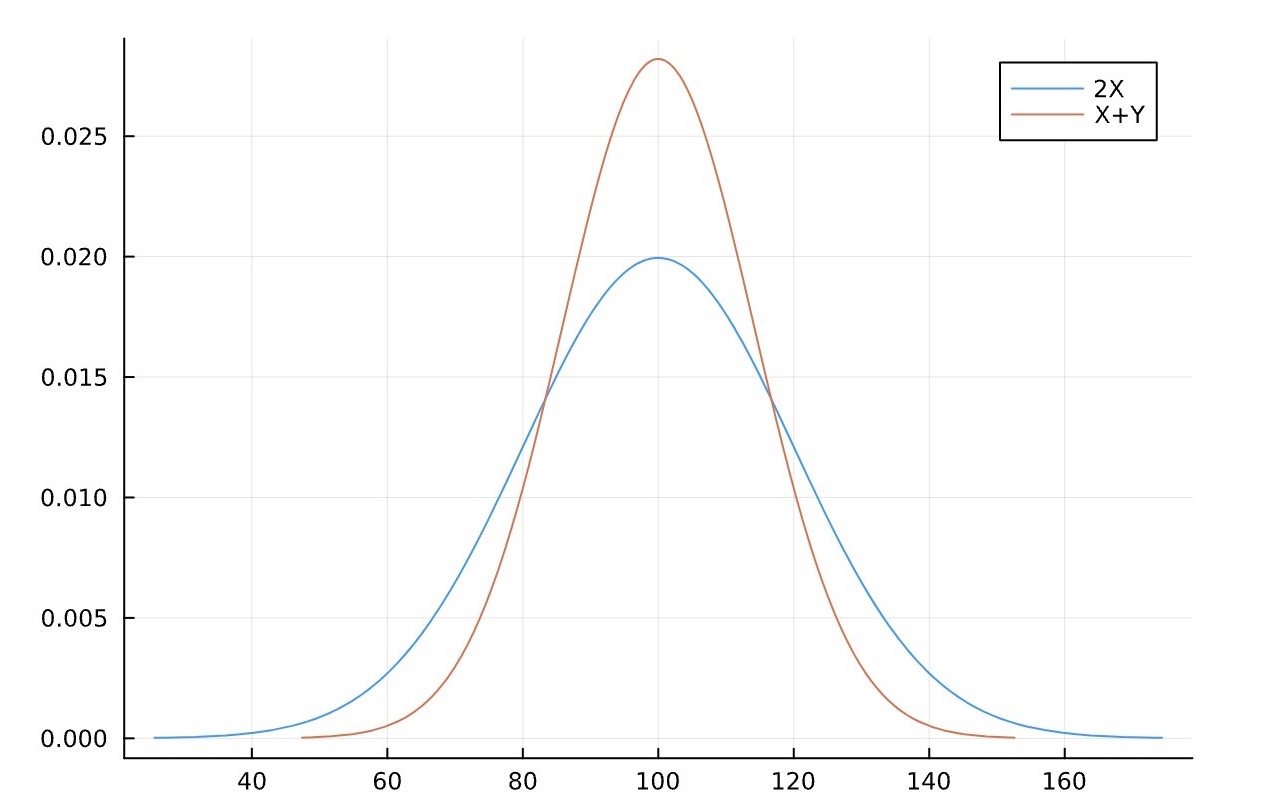
グラフで書いてみると明らかですね。
しかし,ここで,ちょっと疑問が湧きます。(このテストって英語100点,数学100点満点だよね...200点以上はどうするんだろう?)ということでした。
平均点の高いテスト
データの準備
生徒の平均点が高いと,担当者(教員)は嬉しいものです。ちょっと平均点が高いデータ(N=200)を準備しました。
data =[
80
80
53
74
58
46
86
79
81
100
85
94
95
67
71
84
89
100
84
62
74
89
100
80
82
94
100
95
100
82
63
95
72
62
95
99
87
95
100
100
82
40
97
72
100
81
90
90
60
87
75
81
96
80
100
80
73
82
58
87
94
91
85
90
66
90
88
62
100
88
32
95
100
85
87
62
82
71
89
65
100
83
40
98
99
75
82
100
93
81
100
55
100
66
98
99
100
65
99
95
58
90
90
93
99
82
86
94
99
85
58
73
85
90
53
84
54
84
68
88
96
63
67
84
91
95
75
70
58
100
80
80
95
96
92
89
81
100
60
98
89
60
78
58
97
97
100
85
97
92
95
100
95
89
97
94
97
97
97
91
92
96
99
87
97
97
93
87
97
97
98
93
97
97
88
97
92
100
95
100
97
100
97
97
100
97
96
97
92
80
87
95
97
90
80
97
100
93
89
100
]
200-element Vector{Int64}:
80
80
53
74
58
46
86
79
81
100
⋮
95
97
90
80
97
100
93
89
100
データの平均μと標準偏差σを求めてグラフを見てみてる。
まず,データの平均μと標準偏差σを求めて,正規分布
- 平均 μ = 85.805
- 標準偏差 σ = 14.25226210115433
using Distributions , StatsPlots
# data 0〜100点がつくテスト。N=length(data)=200
μ = mean(data) #平均 μ = 85.805
σ = std(data,corrected = false) #標準偏差 σ = 14.25226210115433
f(x) = count(t->(t==x),data)/length(data) #確率質量関数
bar([f(i) for i =0:100],label="PD") #確率分布(PD)
plot!(Normal(μ,σ),lw=2,label="N(μ,σ²)") #正規分布 N(μ , σ^2)
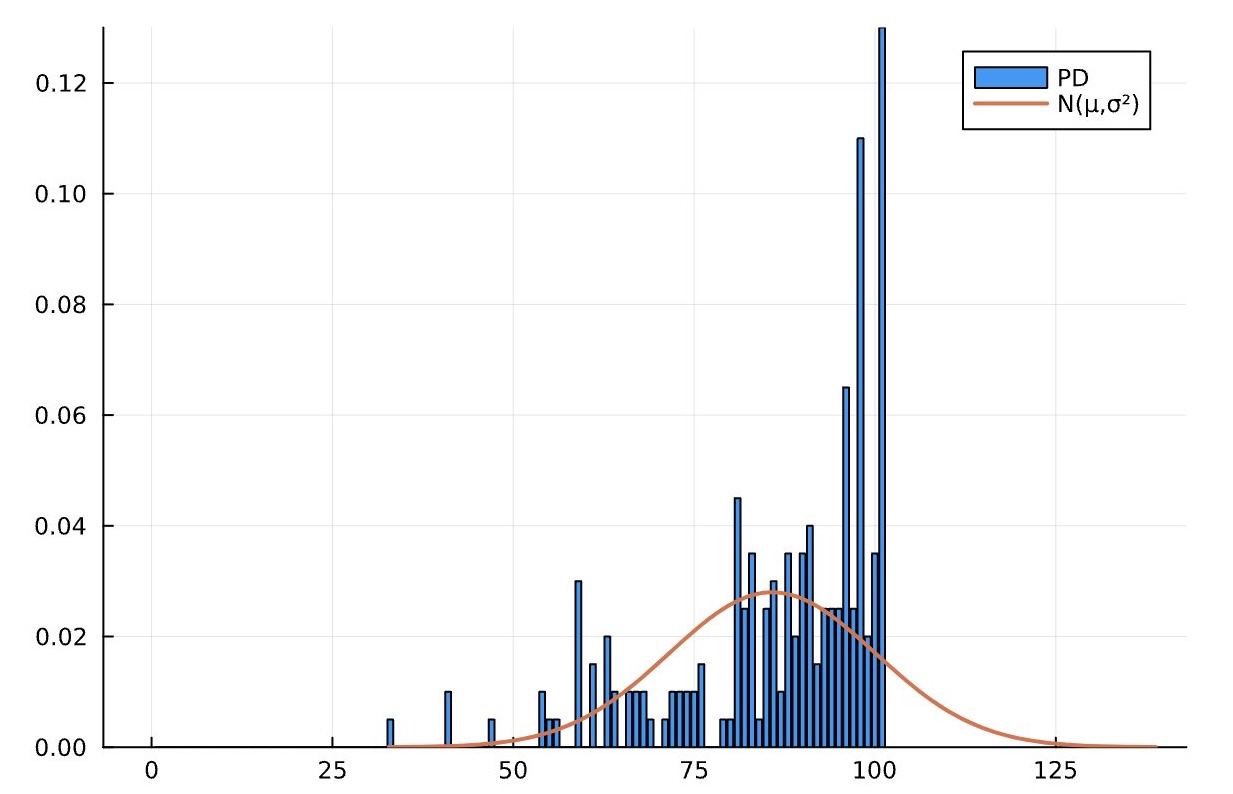
グラフを見た時に,「これは正規分布とみなすわけにはいけないな。」と思いました。また,「100点以上はないから,そこで,点数は途切れる。でも正規分布は100点以上の点数を想定しているようね...」と感じました。
Xにポストする
そこで,これらの疑問をXに投げてみました。
すると,@genkurokiさんから次のような指摘がありました。
改めてテストの得点の分布について考えてみる
@genkurokiさんのコメントを受けて,教科書を確認しました。
教科書の問題
数研出版の数学Bの教科書の「統計的な推測」に次のような問題があります。
生徒の得点を正規分布とみなして,条件の割合を求める問題です。(後で気づいたのですが,100点満点とは書いてありません。120点や-20点などあり得ます)
juliaによる解答
using Distributions
μ = 64
σ = 14
X = Normal(μ,σ)
n = 400/(1-cdf(X,36)-ccdf(X,92)) |> round |> Int
m = ccdf(X,50) * n |> round |> Int
println("(1) 受験者の総数は約$(n)人です。")
println("(2) 合格者は約$(m)人です。")
(1) 受験者の総数は約419人です。
(2) 合格者は約353人です。
新たな問題設定とjuliaでのチェック
そこで,次のような問題を作成してみました。
using Distributions
μ , σ = 85.6 , 14.3
X = Normal(μ,σ)
println("正規分布からの人数 $(ccdf(X,90)*200)")
println("データからの人数 $(count(i->(i≥90),data))")
正規分布からの人数 75.831647352629
データからの人数 103
この結果はかなり差があると思いました。
考察
私としては,今回の場合,「これらの得点の分布を正規分布とみなし,90点以上の人数を求めることはよくないのではないか?」 と考えたわけです。
「正規分布ではない別の分布のモデルが良いのでは?」 と思いました。
そうすると次の疑問があります。私たちが作問する時に,「得点の分布を正規分布とみなせるようなデータが本当にあるのか?」 ということが気になりました。正規乱数でサンプルを求めると,当然,0点以下や100点以上のデータもあるので,それならば,ある程度実現可能なのかなあと思います。
でも私たちが受けるテストは通常,0点以下や100点以上の得点はないので,例えば,今回のように平均点が100点に近いようなものは正規分布とみなし,条件を満たす人数を求めることは適さないのではないかと考えました。
ブートストラップ法
ということで,@genkurokiさんから教えてもらった,ブートストラップ法 となります。まあ,グラフを見て,「これは正規分とみなすのは難しいようね」となれば,こちらを試すのがいいのかなあと思いました。
問題作成とJuliaのコード
次のような問題にしてみました。
コードはChatGPT4oに手伝ってもらいました。
using Random, Statistics
# 200人の0~100点のデータ
# ブートストラップ法のパラメータ
n_bootstrap = 1000 # ブートストラップのサンプル数
n_data = length(data)
# ブートストラップで計算する割合を格納する配列
bootstrap_ratios = zeros(n_bootstrap)
# ブートストラップサンプリングと割合の計算
for i in 1:n_bootstrap
resample = data[rand(1:n_data, n_data)] # 元データからリサンプリング
bootstrap_ratios[i] = mean(resample .>= 90) # 90以上の割合を計算
end
# 信頼区間の計算 (例: 95%信頼区間)
ci_ratio = (quantile(bootstrap_ratios, 0.025), quantile(bootstrap_ratios, 0.975))
# 結果を表示
println("元データで90以上の割合: $(mean(data .>= 90))")
println("ブートストラップ推定の平均割合: $(mean(bootstrap_ratios))")
println("95%信頼区間: [$(ci_ratio[1]), $(ci_ratio[2])]")
元データで90以上の割合: 0.515
ブートストラップ推定の平均割合: 0.5145200000000001
95%信頼区間: [0.445, 0.58]
この結果はとてもいい感じです。
Discussion