Juliaで二項分布を正規分布・ポアソン分布で近似する

はじめに

高校の数学Bの教科書に『確率分布と統計的な推測』という分野があります。新課程ではいよいよこの分野も多くの生徒が共通テストで利用することになります。統計の分野は，高校の現場の先生もそれほど多く授業をやっていません。教科書を見ながら，疑問に思ったこと，その理由を確認しておく必要があります。

この統計の分野は書いてあることの理由が、よくわからないことが多いです。

今回取り上げるのは『二項分布を正規分布で近似する』というところです。

数研出版の数学Bの教科書の説明を見てみます。

『$n$を大きくすると，正規分布のグラフに似てきますね。』

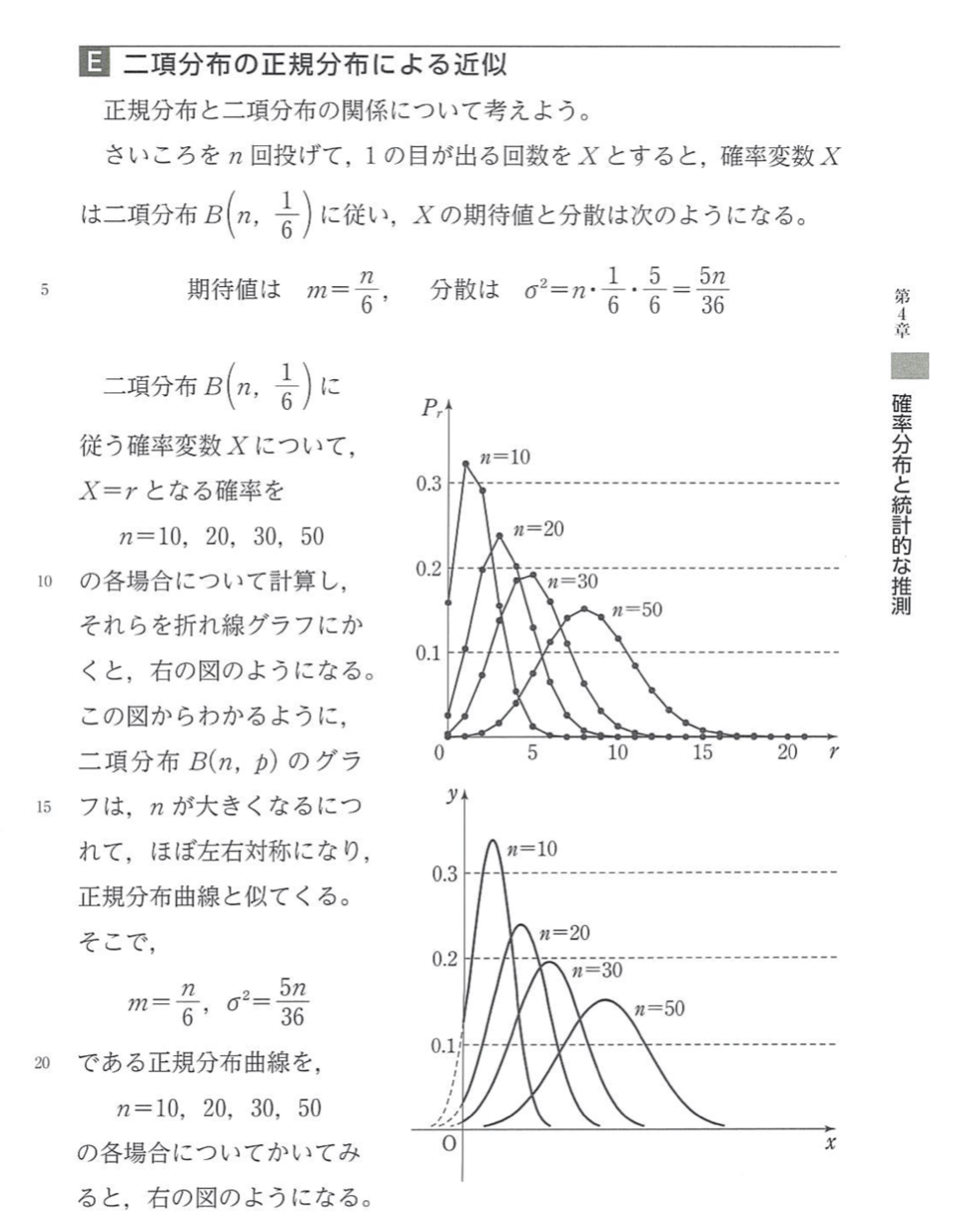
と書いてあります。そして，それを受けて，次のようにまとめてあります。

二項分布$B(n,p)$に従う確率変数$X$は，$n$が大きいとき近似的に正規分布$N(np,npq)$に従う。ただし，$q=1-p$である。

まず，ここで思うことは 『$n$がどのくらい大きいければ近似していいのだろうか？』 ということでした。「$n=8$くらいではダメなのかな？」とかその辺りのことは教科書から全くわかりません。

この後に例題となるわけですが，特に，近似の基準の説明もなく，正規分布を用います。（まあ，流れからするとそうするわけですが．．．）

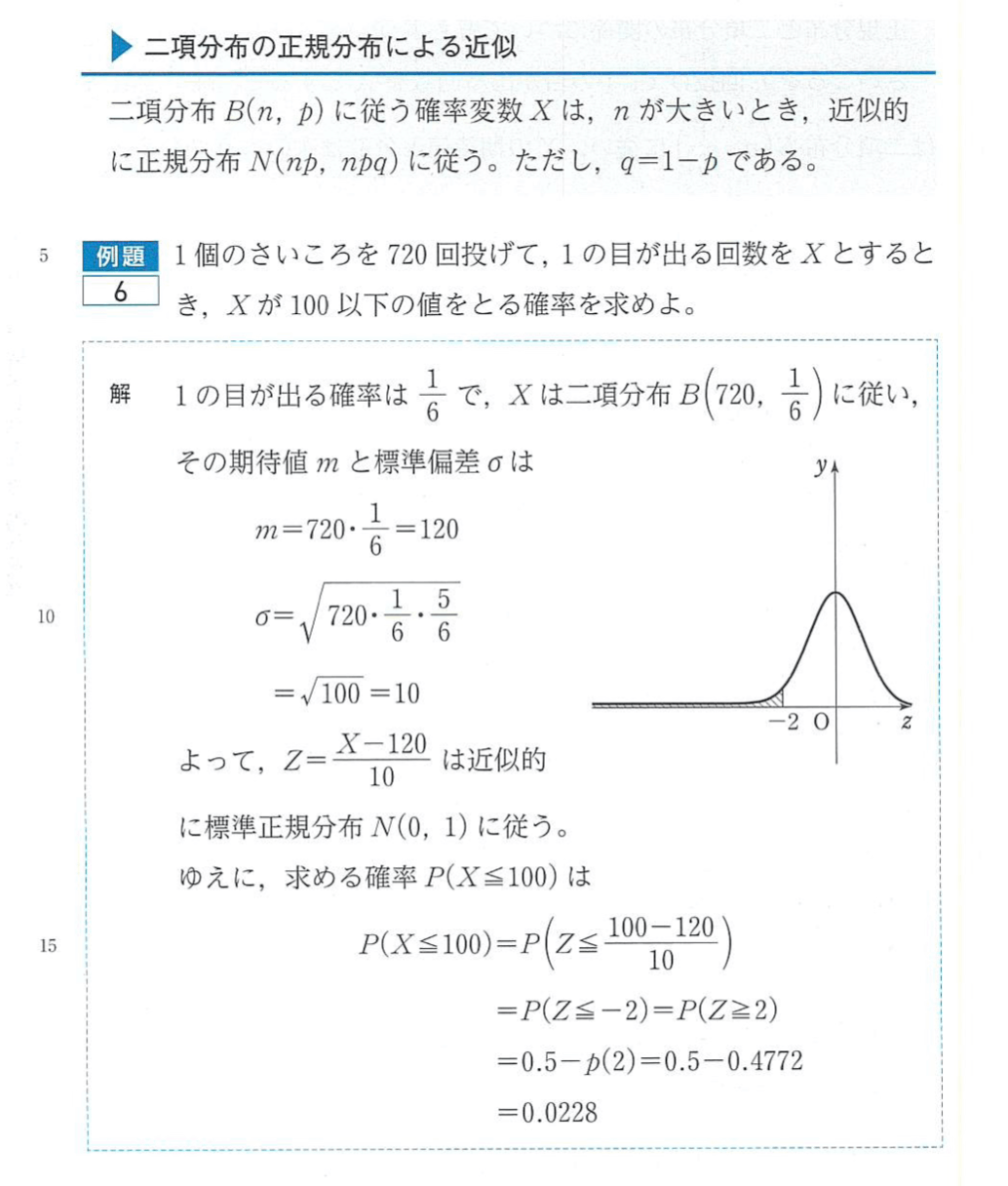
そこで，これらの疑問を解消するべく，調べることにしました。

正規分布・ポアソン分布

まず，二項分布をWikipediaで見てみると，

https://ja.wikipedia.org/wiki/二項分布

正規分布で近似できるのは

『$n$が十分大きくかつ，期待値$np$および分散$np(1−p)$も十分大きい場合』

との記載がありました。そしてその下に，ポアソン分布の説明があり，二項分布がポアソン分布で近似できる条件が書いてありました。

『$n$が十分大きく，$p$が十分小さい場合」

そして，『$\lambda =np$が適度な大きさになるため〜』とあったので「$n$と$p$の比率が関係するのかな？」と考えて，さらにポアソン分布をWikipediaで見てみると，

https://ja.wikipedia.org/wiki/ポアソン分布

$\lambda =np$が大きい値のときはポアソン分布は正規分布で近似できる。

とありました。

ということで，『二項分布を正規分布・ポアソン分布に近似するときの基準はあるのか？」 ということを調べることにしました。

二項分布を正規分布・ポアソン分布に近似するときの基準

ネットで色々探したのですが，どうも，『統計分布ハンドブック』という書籍に色々書いてあるのではないか？と行き着いたのですが，残念ながら読めていません。

https://www.asakura.co.jp/detail.php?book_code=12178

二項分布を正規分布で近似するときの条件

次のような記述を以下のサイトで見つけました。『統計分布ハンドブック』を参考にしたようです。

https://atarimae.biz/archives/7922

正規分布の近似基準は3つの条件のうち少なくとも1つを満たすことのようです。

1. $\min(np,nq)>10$
2. $0.1\leqq p\leqq 0.9$ かつ $npq>5$
3. $npq>25$

二項分布をポアソン分布で近似するときの条件

次のような記述を以下のサイトで見つけました。

https://navaclass.com/poisson/

ポアソン分布の一般的近似基準は次の条件を満たすことのようです。

$n>50$ かつ $np≦5$

まとめ

とりあえず，条件はわかったので，下の表の4パターンについて調べることにしました。

正規分布／ポアソン分布	◯	×
○	？	$n=720$，$p=1/6$
×	$n=400$，$p=0.01$	$n=8$，$p=0.5$

『正規分布，ポアソン分布のどちらで近似できる条件』考えるにあたり，$np≦5$という条件がかなり厳しくて，このサイトの一般的近似基準は 『正規分布ではなくポアソン分布を利用するときの基準ではないか？』 と推測しました。そこで，今回，ポアソン分布の近似基準を

$n>50$ かつ $p<0.1$

とすることにしました。調べる4パターンは次のようになります。

正規分布／ポアソン分布	◯	×
○	$n=10000$，$p=0.01$	$n=720$，$p=1/6$
×	$n=400$，$p=0.01$	$n=8$，$p=0.5$

Juliaを使って二項分布$B(n,p)$の確率$P(X\leqq k)$を求める

julia を使って二項分布$B(n,p)$で$P(X\leqq k)$の確率を近似的に求めます。分布もグラフで図示することにしました。黒木さん（@genkuroki）に教えてもらったコードを参考にしています。

https://twitter.com/genkuroki/status/1557367851735953409

approx.jl

using Distributions
using StatsPlots

function approx(n,p,k)
   dist = Binomial(n,p)
   λ = n*p
   dist2 = Poisson(λ)
   μ,σ = mean(dist),sqrt(var(dist))
   dist3 = Normal(μ,σ)
   
   ymax = map(x -> pdf(dist3,x), μ)
   
   @show mean(dist),var(dist)
   @show rationalize.((mean(dist),var(dist)))

   xs = support(dist)
   bar(xs,dist,title="",label="$dist",ylim=(0,ymax*1.3),xlim=(μ-5σ,μ+5σ),color="skyblue")
   println("二項分布よりP(X≦$k)=",cdf(dist,k))

   println("正規分布よりP(X≦$k)=",cdf(dist3,k))
   plot!(dist3,title="",label="$dist3",ylim=(0,ymax*1.3),xlim=(μ-3σ,μ+3σ),color="red")


   println("ポアソン分布よりP(X≦$k)=",cdf(dist2,k))
   scatter!(dist2,title="",label="$dist2",ylim=(0,ymax*1.3),xlim=(μ-5σ,μ+5σ),color="red")
end

（ケース1）$n=720$，$p=1/6$，$k=100$

これは先ほど紹介した教科書にあった例題です。

1個のさいころを720回投げて，1の目が出る回数を$X$とするとき，$X$が100以下の値を取る確率を求めよ。

$np=120$，$npq=100$となり，

• ○　正規分布
• ×　ポアソン分布

の場合です。

approx(720,1/6,100)

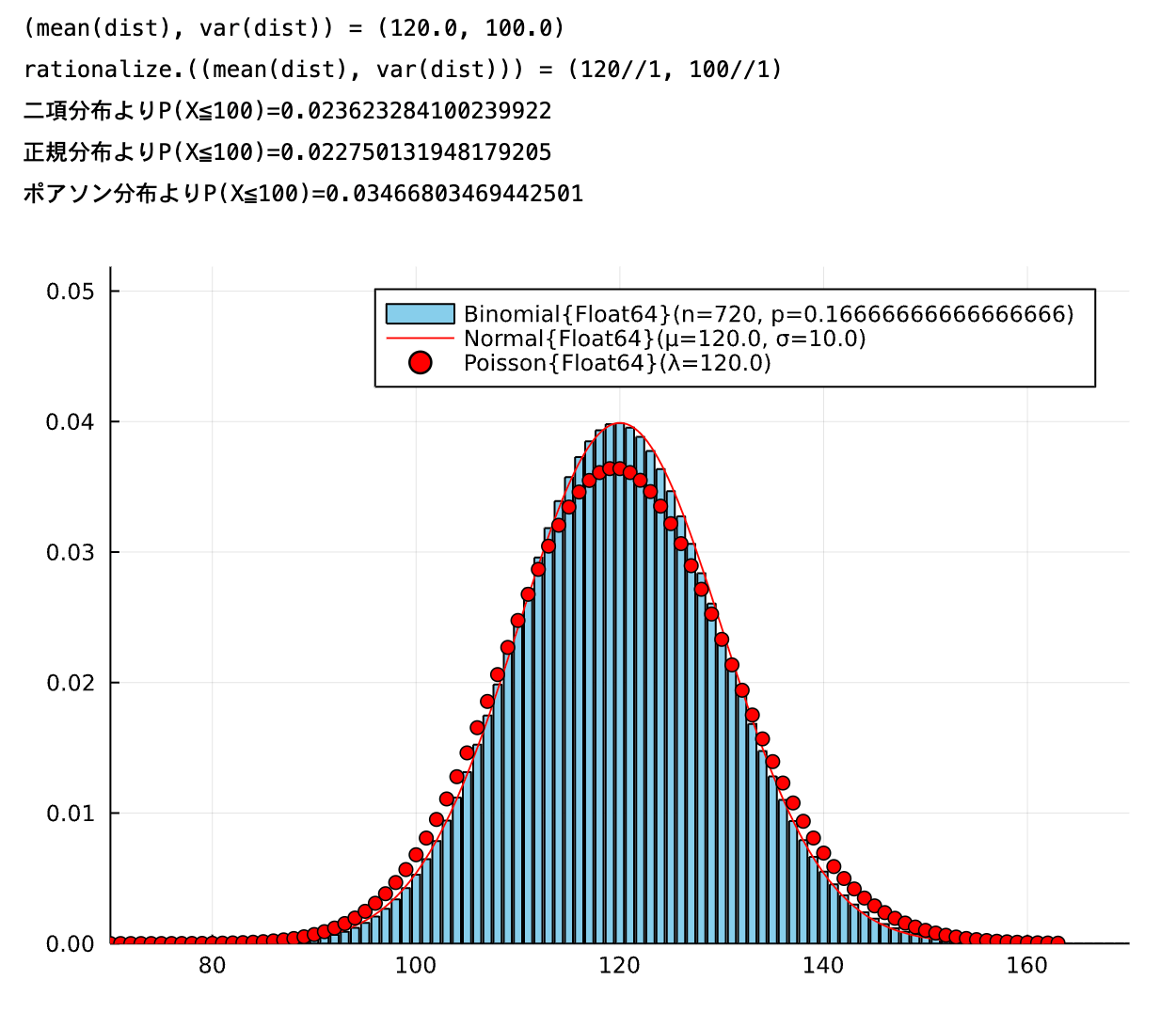
ポアソン分布はちょっとズレてますね。

（ケース2）$n=8$，$p=0.5$，$k=3$

$np=4$，$npq=2$となり，

• ×　正規分布
• ×　ポアソン分布

の場合です。

approx(8,0.5,3)

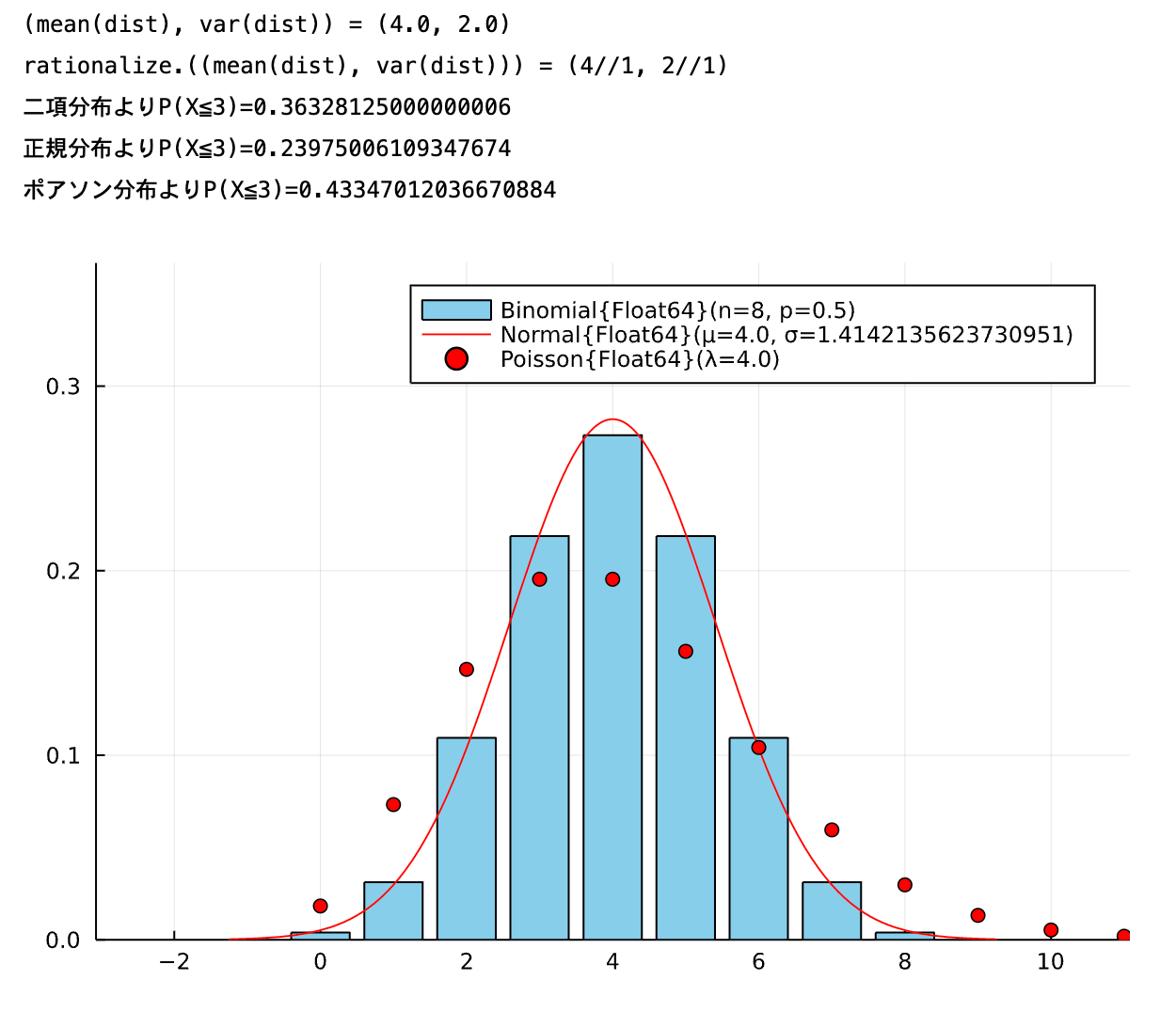
まあ，$n$があまり大きくないですね。こういうときは近似ではなく，二項分布より求めるということでしょうか。

（ケース3）$n=400$，$p=0.01$，$k=2$

$np=4$，$npq=3.96$となり，

• ×　正規分布
• ○　ポアソン分布

の場合です。

approx(400,0.01,2)

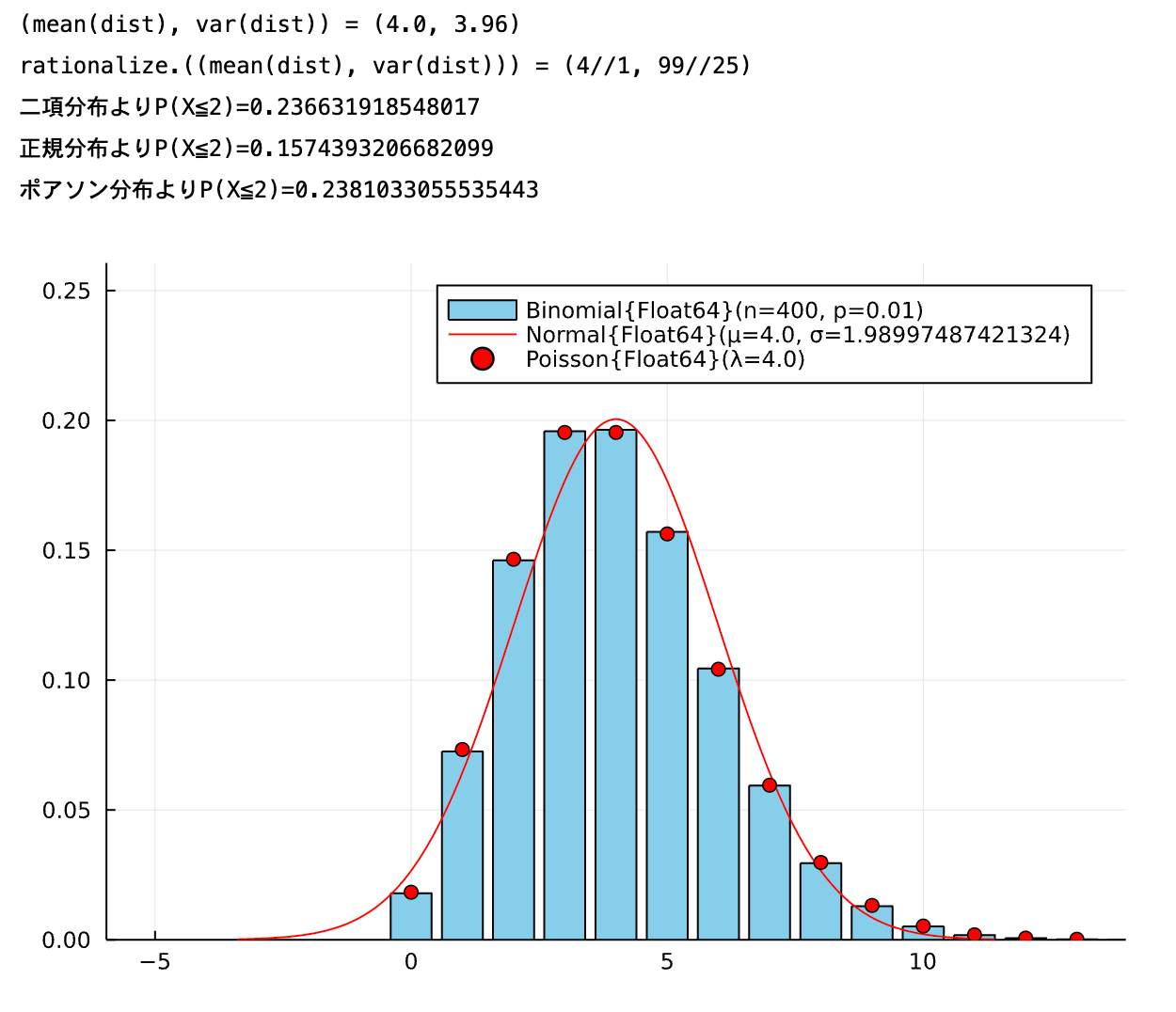
ポアソン分布は平均と分散が等しいので，$np$と$npq$がほぼ同じ値の時に近似できそうです。そのために，『$p$が十分小さい』という条件があるようですね。

（ケース4）$n=10000$，$p=0.01$，$k=80$

$np=100$，$npq=99$となり，

• ○　正規分布
• ○　ポアソン分布

の場合です。

approx(10000,0.01,80)

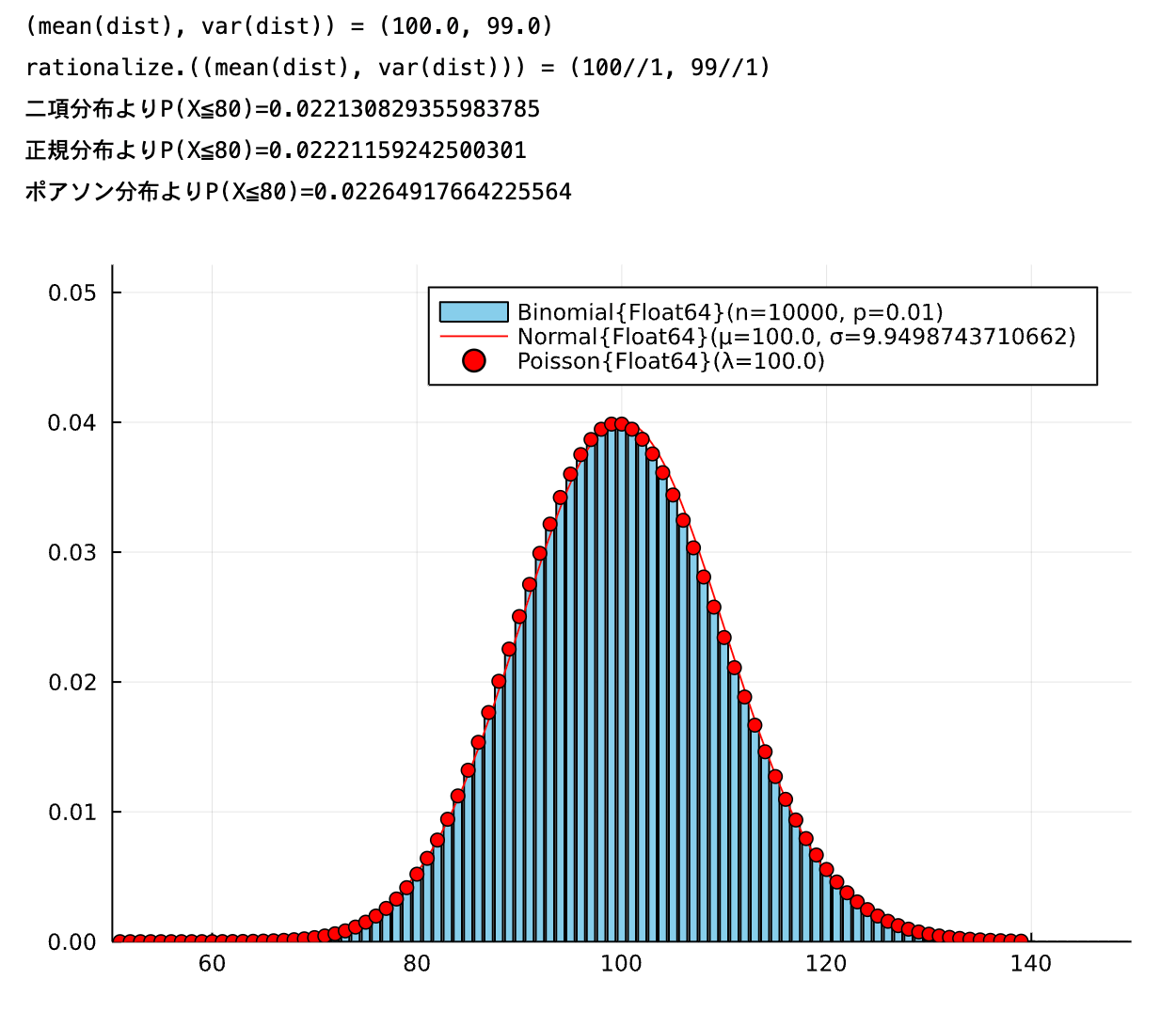
正規分布・ポアソン分布のどちらでもよさそうです。このようなときには正規分布を使うのでしょうね。

まとめ

調べてみてよかったと思います。教科書などでは$n$が大きいと考えて二項分布を正規分布へ近似する流れとなっているわけですが，（ケース3）からわかるように，$n$大きくても，$p$が小さいと，正規分布は近似とは言えません。二項分布$B(400,0.01)$の確率$P(X\leqq 2)$の確率をみてみます。

分布	確率
二項分布	0.2366
正規分布	0.1574
ポアソン分布	0.2381

私たちが，自分で問題を作成するときに知っておかないと，近似とは言えない確率を求めていることになります。

今回，近似するときの基準を探しましたが，そもそも，個々の近似が適切かどうか調べる指標があるはずです。（検定？適合度検定？）この辺りはもう少し調べてみたいと思います。