今日の数列（解説編）

$$\prod_{k=1}^{n-1}2\sin\frac{k\pi}n=n$$

はじめに

理系の高校2年生を対象にした実力テストで，複素数平面の問題を出題しました。生徒の解答を見ながら，まとめた内容になります。

問題

複素数平面上の単位円（$\text{O}$ を中心とする半径1の円）に正 $n$ 角形が内接している。

正 $n$ 角形の頂点 $\text{A}_k\,(k=0,1,2,\cdots,n-1)$ を表す複素数は$\displaystyle{z_k=\cos\frac{2k\pi}n+i\sin\frac{2k\pi}n}$ である。

今，$1\leqq k\leqq n-1$ として，線分 $\text{A}_0\text{A}_k$ の長さを $L_k$ とする。次の問いに答えよ。

1. $n=3$ （正三角形）のとき，2個の線分の長さの積 $L_1\times L_2$ を求めよ。
2. $n=4$（正方形）のとき，3個の線分の長さの積 $L_1\times L_2\times L_3$ を求めよ。
3. $n\geqq3$ として，$n-1$ 個の線分の長さの積 $L_1\times L_2 \times \cdots \times L_{n-1}$ を求めよ。

答え

1. $L_1\times L_2=3$
2. $L_1\times L_2\times L_3=4$
3. $L_1\times L_2 \times \cdots \times L_{n-1}=n$

解説

1. $L_1=L_2=\sqrt3$

   

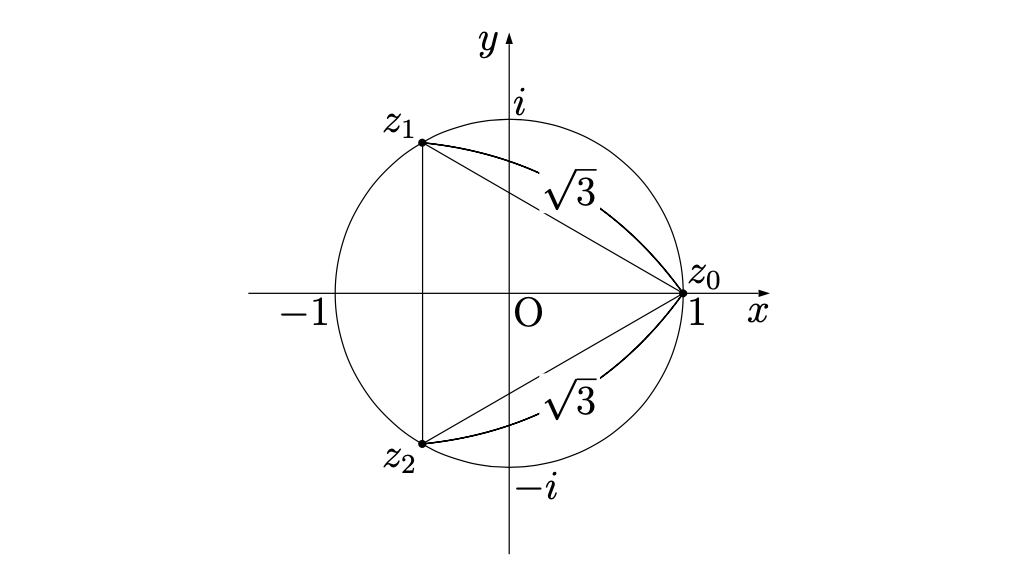
   $$\therefore L_1\times L_2=\bm{3}$$

2. $L_1=L_3=\sqrt2,\,L_2=2$

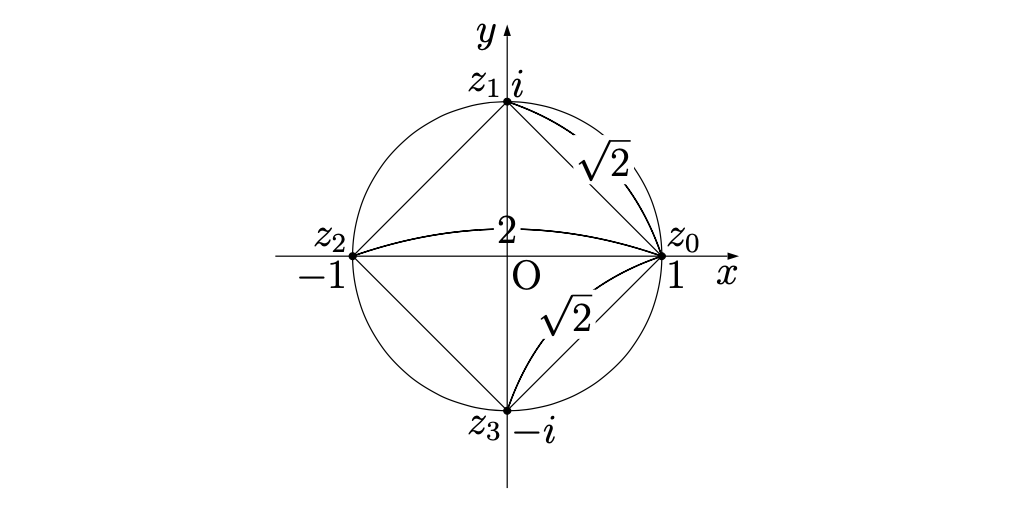
$$\therefore L_1\times L_2\times L_3=\sqrt2\times 2\times \sqrt2=\bm{4}$$

3. $L_k=|z_k-z_0|$

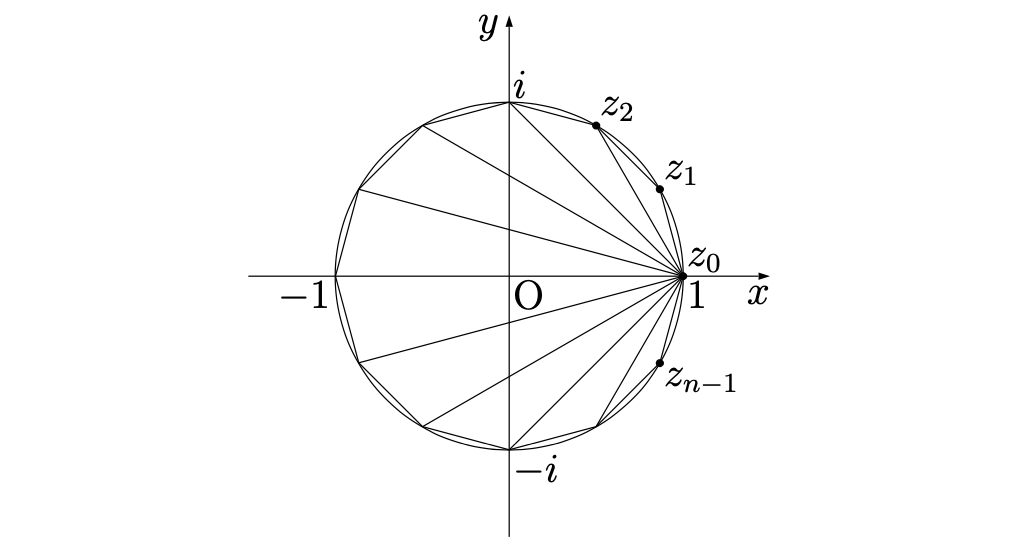
$$\begin{aligned} &L_1\times L_2 \times \cdots \times L_{n-1}\\ &=|z_1-z_0|\times |z_2-z_0|\times \cdots\times |z_{n-1}-z_0|\\ &=|(z_1-1)(z_2-1)\cdots(z_{n-1}-1)|=\bigstar\end{aligned}$$

ここで，方程式$z^n=1$の解は

$$z=z_0,z_1,z_2,\cdots,z_{n-1}$$

である。$z^n=1$は

$$(z-1)(z^{n-1}+z^{n-2}+\cdots+z+1)=0$$

と変形でき，$z_0=1$ であることから，方程式 $z^{n-1}+z^{n-2}+\cdots+z+1=0$ の $n-1$ 個の解は

$$z=z_1,z_2,\cdots,z_{n-1}$$

となるので，

$$(z-z_1)(z-z_2)\cdots(z-z_{n-1})=z^{n-1}+z^{n-2}+\cdots+z+1$$

である。$z=1$とすると，

$$(1-z_1)(1-z_2)\cdots(1-z_{n-1})=\underbrace{1+1+\cdots+1}_{n個}=n$$

$$\therefore \bigstar=|n|=\bm{n}$$

3.での生徒の解答

結論から言うと，次の答えも正解としました。

$$\begin{aligned} L_k&=|z_k-z_1|\\ &=\bigg|\cos\frac{2k\pi}n+i\sin\frac{2k\pi}n-1\bigg|\\ &=\sqrt{\left(\cos\frac{2k\pi}n-1\right)^2+\sin^2\frac{2k\pi}n}\\ &=\sqrt{\cos^2\frac{2k\pi}n-2\cos\frac{2k\pi}n+1+\sin^2\frac{2k\pi}n}\\ &=\sqrt{2-2\cos\frac{2k\pi}n}\\ &=\sqrt{4\cdot\frac{1-\cos\frac{2k\pi}n}2}\\ &=\sqrt{4\sin^2\frac{k\pi}n}\\ &=2\bigg|\sin\frac{k\pi}n\bigg|\\ &=2\sin\frac{k\pi}n\, \left(\therefore 0<\frac{k\pi}n<\pi\right) \end{aligned}$$

よって，

$$\begin{aligned} &L_1\times L_2 \times \cdots \times L_{n-1}\\ &=2\sin\frac{\pi}n\times2\sin\frac{2\pi}n\times\cdots\times2\sin\frac{(n-1)\pi}n\\ &=\bm{\prod_{k=1}^{n-1}2\sin\frac{k\pi}n} \end{aligned}$$

まとめ

このことから，次の等式が成り立ちます。

$$\bm{\prod_{k=1}^{n-1}2\sin\frac{k\pi}n=n}$$

この等式は $n\geqq3$ で議論しましたが，$n\geqq2$ でも成り立ちます。$n=1$ のときも強引に成り立つと考えてもいいのですが，それはやめておきます。

Juliaで数値計算！

やっぱり，Juliaで計算してみたいです！

function ff(n)
    a=1
    for k=1:n-1
        a=a*2*sin(k*π/n)
    end
   println(a)
end

ff (generic function with 1 method)

for n=2:10
    ff(n)
end

2.0
3.0
4.0
5.000000000000001
5.999999999999998
7.0000000000000036
8.000000000000002
9.000000000000004
10.000000000000004

バッチリです！