🔥

M1 macで Julia1.8.1+Wolfram Engine13.1.0

2022/09/11に公開

Julia

math

wolfram

idea

はじめに

juliaのv1.8.1が2022年9月6日に出ました！Wolfram Engineを確認してみるとv13.1.0だったので，こちらもインストールして確認してみようと思います。Julia v1.8.0からmacOS ARM (M-series Processor)に対応したものがでています。Wolfram Engineはv13.0.0を使っていたのですが，コチラも新しいものを使ってみたいと思います。

https://julialang.org/downloads/

julia v1.8.1のインストール

Macなのでダウンロードして，アプリケーションのフォルダにドラッグして完了です。（簡単！）

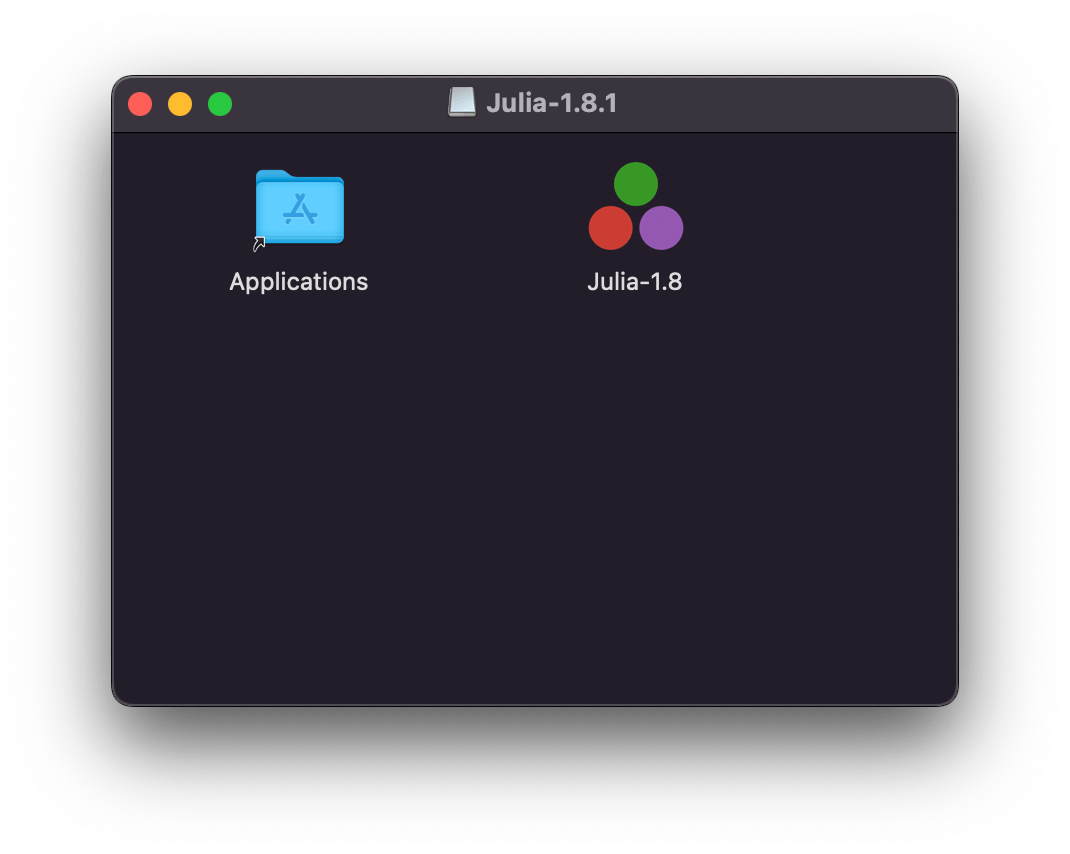
その後，REPLで立ち上げてpkgモードでadd IJuliaとしてJupyter notebookで利用できるようにします。私はVSCodeで利用しています。

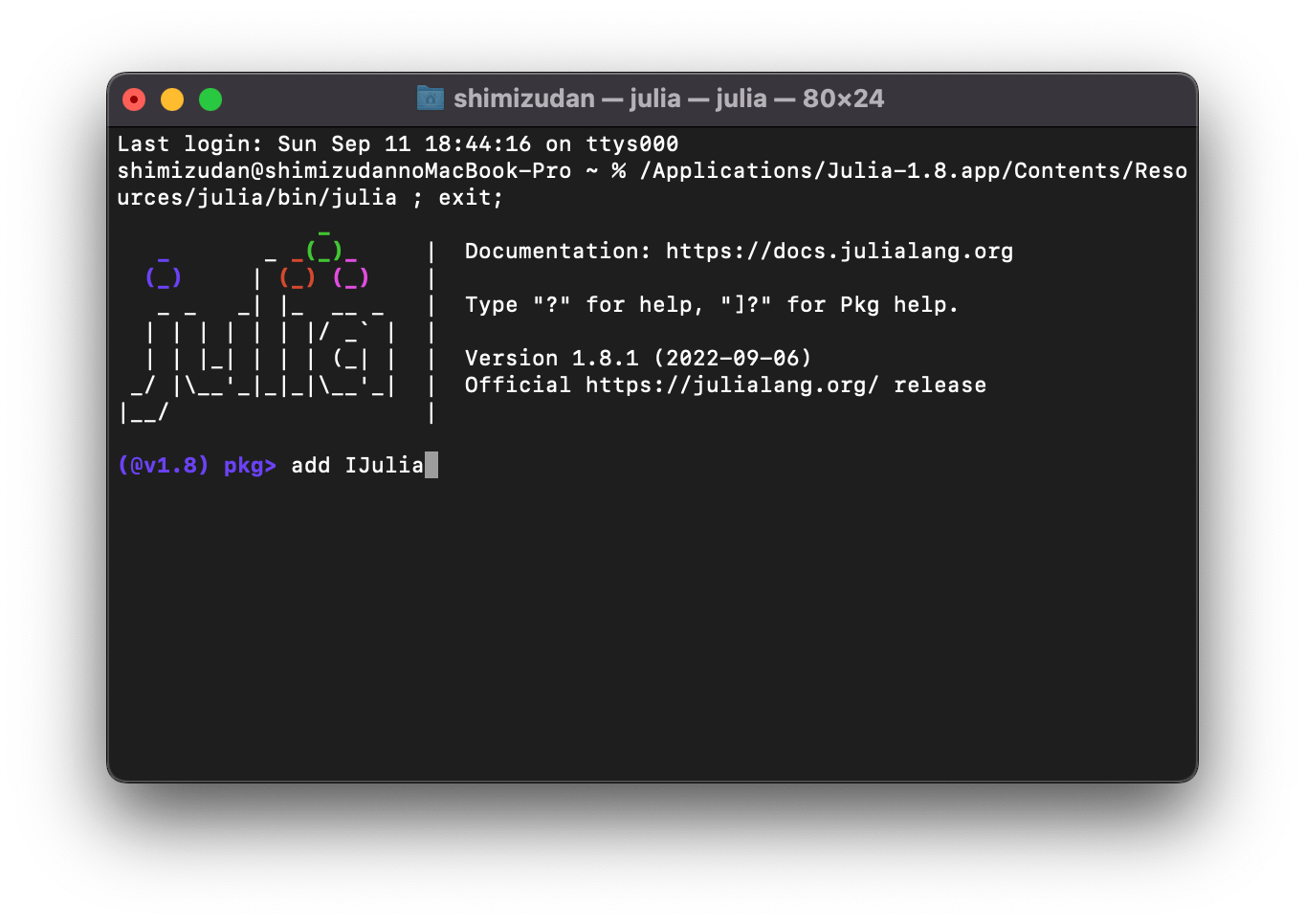
ちゃんとJulia 1.8.1が表示されました！

Wolfram Engine13.1.0のインストール

まず，先ほどのサイトからダウンロードします。

その後，インストールになります。インストールの感じが前と違うような気がします．．．

アプリケーションフォルダにドラッグすると，前のバージョンと置き換えていいか聞かれる。置き換えることにします。wolframScriptもインストールしました。

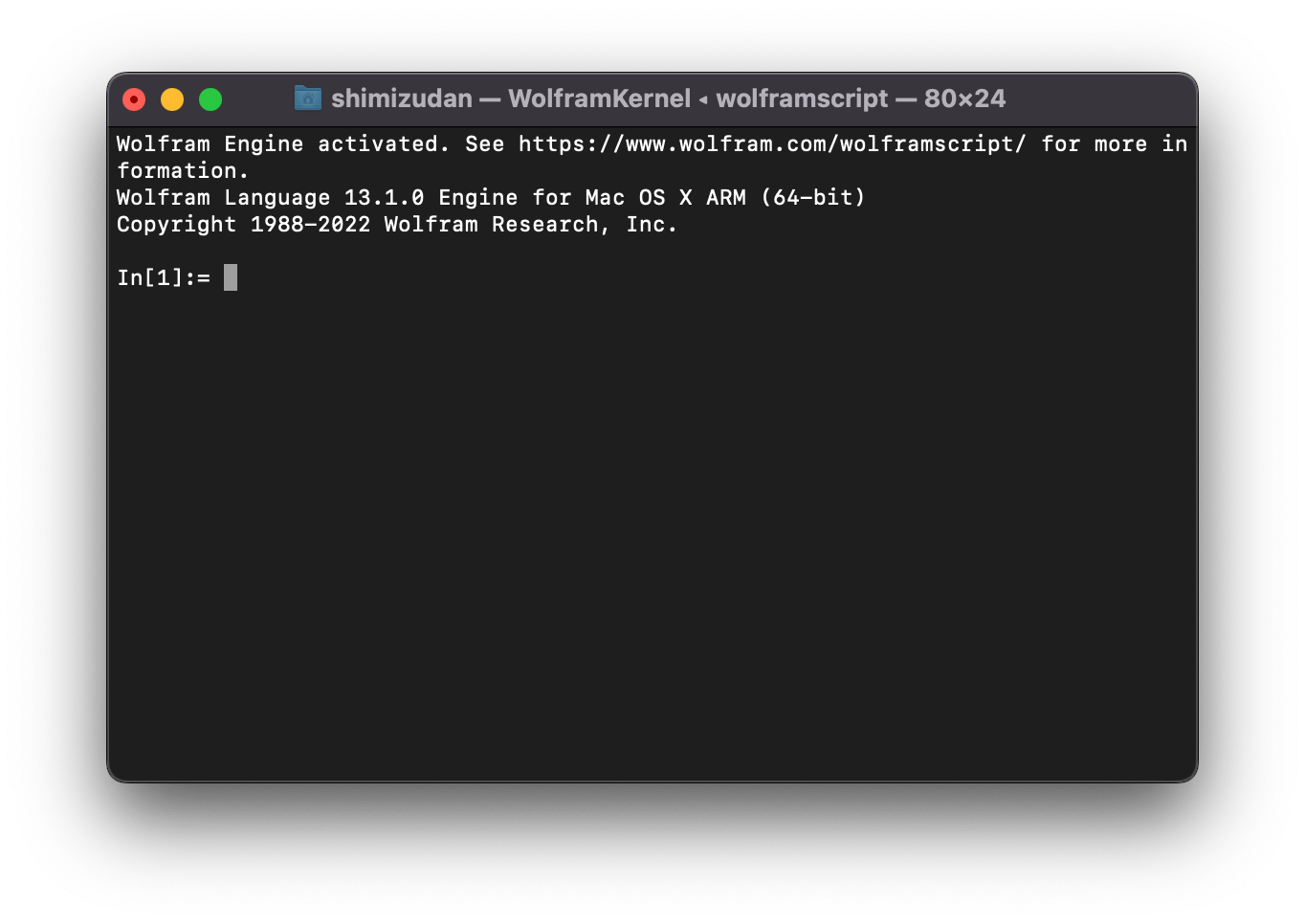
無事にWolfram Engine13.1.0は起動しました。
表示を見るとWolfram Language 13.1.0 Engine for Mac OS X ARM (64-bit)
となっています。M1 macに対応しているように思えます。

VSCode内の.ipynbファイルでJulia上でWolfram Engineを使う。

以前，Engine13.0.0を使っていたので，特に何か変更することはなさそうです。

初めてJupyter notebookでWolfram Engineを利用するときは次のサイトを参考にしました。
Method 2を利用して設定しました。

初めてJuliaでWolfram Engineを利用する方は，次のサイトが参考になると思います。

利用例

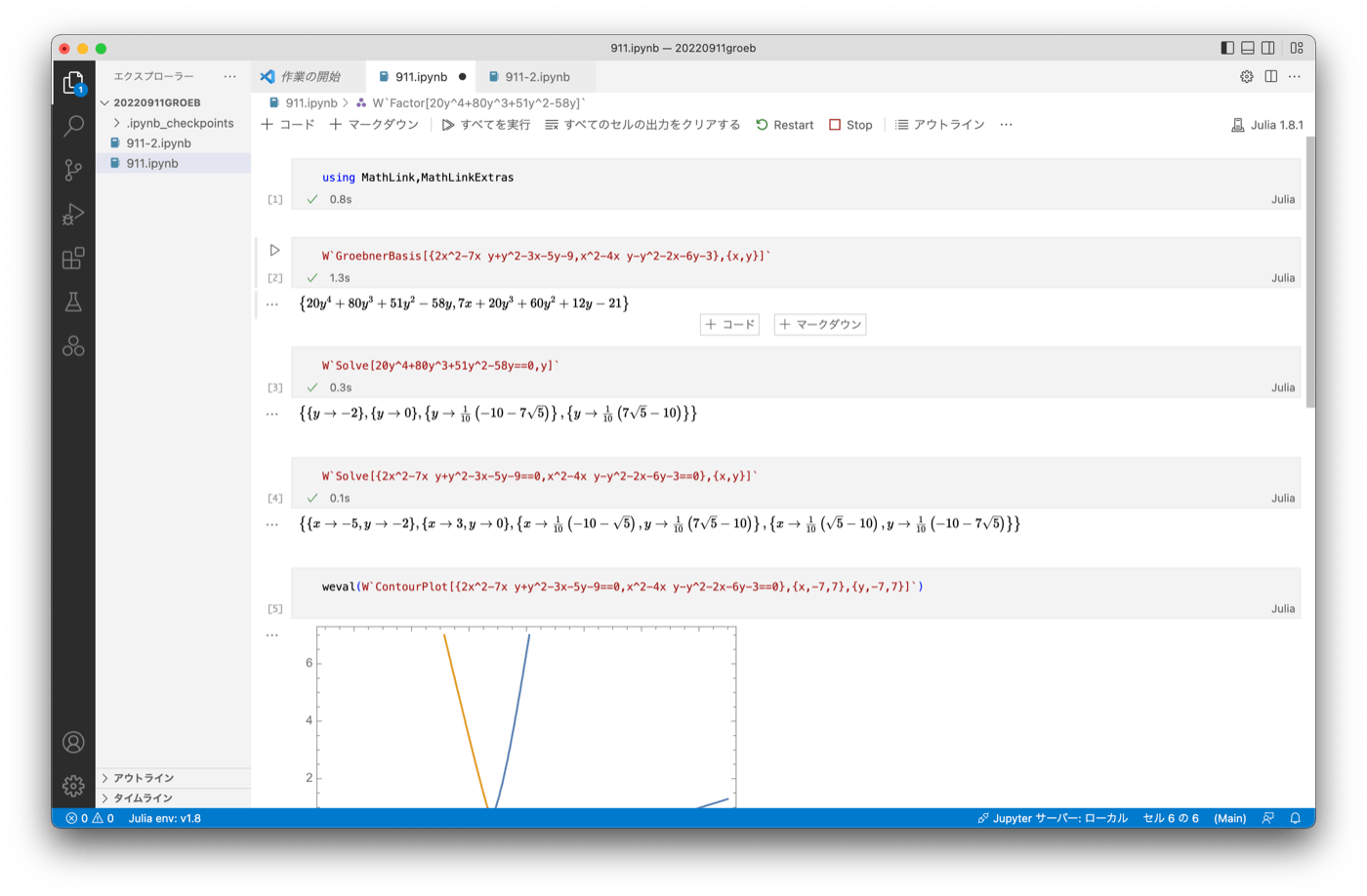
Twitterで面白そうな連立方程式があったので，解いてみました。

まずはjulia上での利用するパッケージを読み込む

2つのパッケージを読み込みます。

using MathLink,MathLinkExtras

グレブナー基底を調べてみる

W`GroebnerBasis[{2x^2-7x y+y^2-3x-5y-9,x^2-4x y-y^2-2x-6y-3},{x,y}]`

\left\{20 y^4+80 y^3+51 y^2-58 y,7 x+20 y^3+60 y^2+12 y-21\right\}

W`Solve[20y^4+80y^3+51y^2-58y==0,y]`

\left\{\{y\to -2\},\{y\to 0\},\left\{y\to \frac{1}{10} \left(-10-7\ \sqrt{5}\right)\right\},\left\{y\to \frac{1}{10} \left(7\ \sqrt{5}-10\right)\right\}\right\}

連立方程式として解いてみる

W`Solve[{2x^2-7x y+y^2-3x-5y-9==0,x^2-4x y-y^2-2x-6y-3==0},{x,y}]`

\left\{\{x\to -5,y\to -2\},\{x\to 3,y\to 0\},\left\{x\to \frac{1}{10}\ \left(-10-\sqrt{5}\right),y\to \frac{1}{10} \left(7\ \sqrt{5}-10\right)\right\},\left\{x\to \frac{1}{10} \left(\sqrt{5}-10\right),y\to\ \frac{1}{10} \left(-10-7 \sqrt{5}\right)\right\}\right\}

グラフを描いてみる

weval(W`ContourPlot[{2x^2-7x y+y^2-3x-5y-9==0,x^2-4x y-y^2-2x-6y-3==0},{x,-7,7},{y,-7,7}]`)

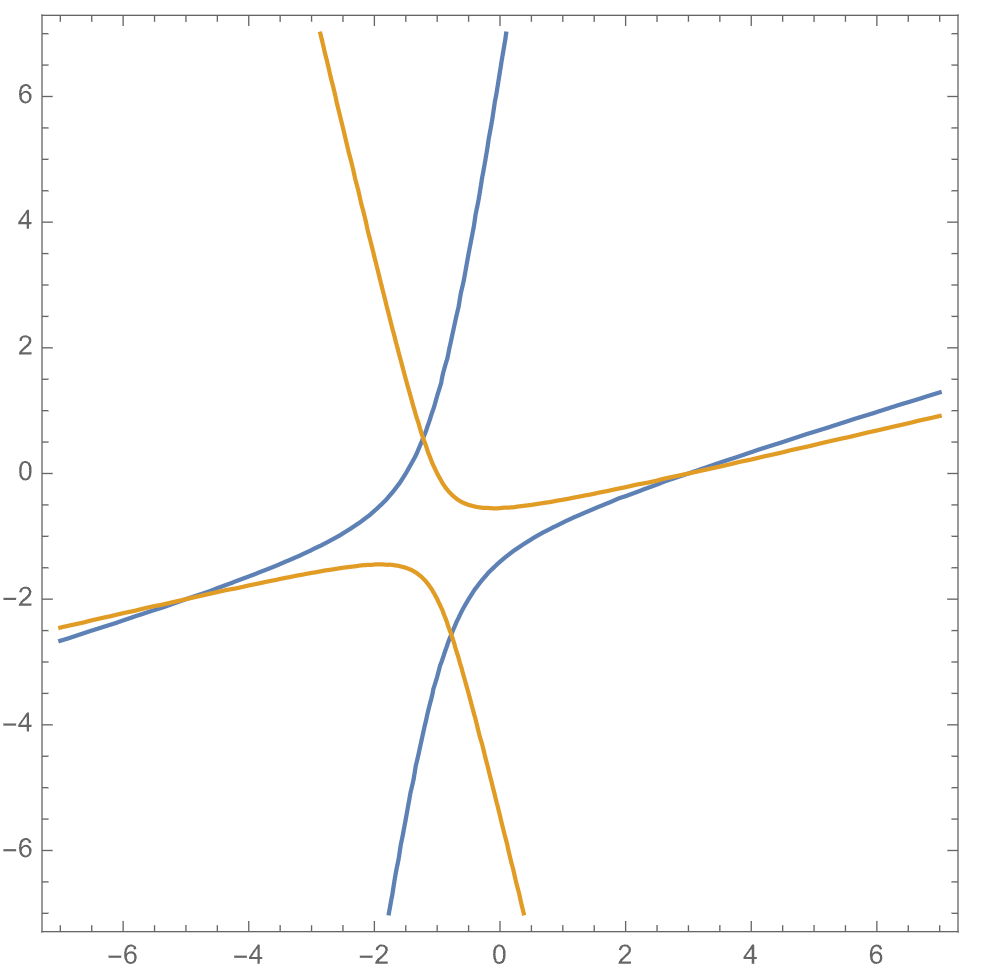
まとめ

jupyter notebook上でWolfram Engineを動かしても，Julia上でWolfram Engineを動かしても，どちらもいい感じです！