🦋

あみだくじの総数をJulia言語で求める。

2025/04/29に公開

 はじめにXのタイムラインであみだくじに関するトピックが流れてきました。
https://x.com/tsatie/status/1916177324254629954
@tsatieさんのポストです。気になったので私も考えてみることにしました。

 あみだくじの総数をどのように考えるのか？まず，思ったのが，「あみだくじの総数はどのように考えるのだろう？」ということでした。
https://x.com/dannchu/status/1916268837097668893
例えば，縦4本，横5本のあみだくじを上から順々に横の位置を決めていくのであれば，
左側は(12)(34)(23)(12)(23)
左側は(34)(12)(23)(12)(23)
となり，異なります。このように考えて，あみだくじの総数や確率を考える立場もいろいろあることがわかりました。こちらの数え方に基づく記事を紹介します。
https://manabitimes.jp/math/1157
私自身もこちらの立場で，以前記事を書いていました。
https://zenn.dev/dannchu/articles/7175d46869231b
今回，@tsatieさんに確認したところ，この立場ではなく，「このような2つは同一視する（1通りと数える）」とのことでした。
https://x.com/tsatie/status/1916315776098963955
これは面白そうです。

 あみだくじの総数の数え方@tsatieさんは数え方に関して，すでに知見があって，次のように対応させて考えていました。
!「縦m本, 横線n本の標準的なあみだくじの総数」を数えるのは,「1列に並んだm個の点を行きつ戻りつし, 2n+m−1回で端から端に辿り着く道行」を数えるのと同じである。
詳しくは下記のサイトをご覧ください。
https://amaryllis4u.wordpress.com
@tsatieさんからコードも紹介されたのですが，数が大きくなると遅くなってしまうようだったので，高速化も含めてJulia言語で取り組んでみることにしました。

 Julia言語によるコード化@tsatieさんのコードは以下のサイトです。
https://github.com/tsatie/SatieGitHubTest/blob/master/20250426AmidaCount.ipynb
これを元に，ChatGPT-4oと相談しながらコードを作成しました。

 コードまずは作成したコードです
using PrettyTables

function calculate_amidakuji_distribution(tn::Int, an::Int)
    ln = 2*an + tn

    dp = Dict{Tuple{Int, Vector{Int}}, BigInt}()
    dp[(0, collect(0:tn-1))] = 1

    for step in 1:ln-1
        new_dp = Dict{Tuple{Int, Vector{Int}}, BigInt}()
        for ((h, perm), c) in dp
            if h + 1 <= tn - 1
                key_up = (h + 1, perm)
                new_dp[key_up] = get(new_dp, key_up, 0) + c
            end
            if h >= 1
                newh = h - 1
                perm2 = copy(perm)
                perm2[h], perm2[h+1] = perm2[h+1], perm2[h]
                key_dn = (newh, perm2)
                new_dp[key_dn] = get(new_dp, key_dn, 0) + c
            end
        end
        dp = new_dp
    end

    stat = zeros(BigInt, tn, tn)
    total = 0

    for ((h, perm), c) in dp
        if h == tn - 1
            total += c
            for i in 1:tn
                stat[i, perm[i]+1] += c
            end
        end
    end

    println("\n🧮 あみだくじ統計 (n = $tn, k = $an)")
    println("=============================================")
    println("🔢 総パターン数: $total\n")

    println("📊 ゴール別マッピング (回数)")
    pretty_table(stat; 
        header=["Start $(i+1)" for i in 0:tn-1],
        row_labels=["Goal $(i+1)" for i in 0:tn-1],
        compact_printing=false
    )

    println("\n📈 ゴール別マッピング (確率 %)")
    percents = 100 .* stat ./ total
    percents_float = Float64.(percents)
    pretty_table(round.(percents_float; digits=3);
        header=["Start $(i+1)" for i in 0:tn-1],
        row_labels=["Goal $(i+1)" for i in 0:tn-1],
        compact_printing=false
    )

    println("=============================================\n")
end


 具体例# 縦線8本，横線10本
calculate_amidakuji_distribution(8,10)
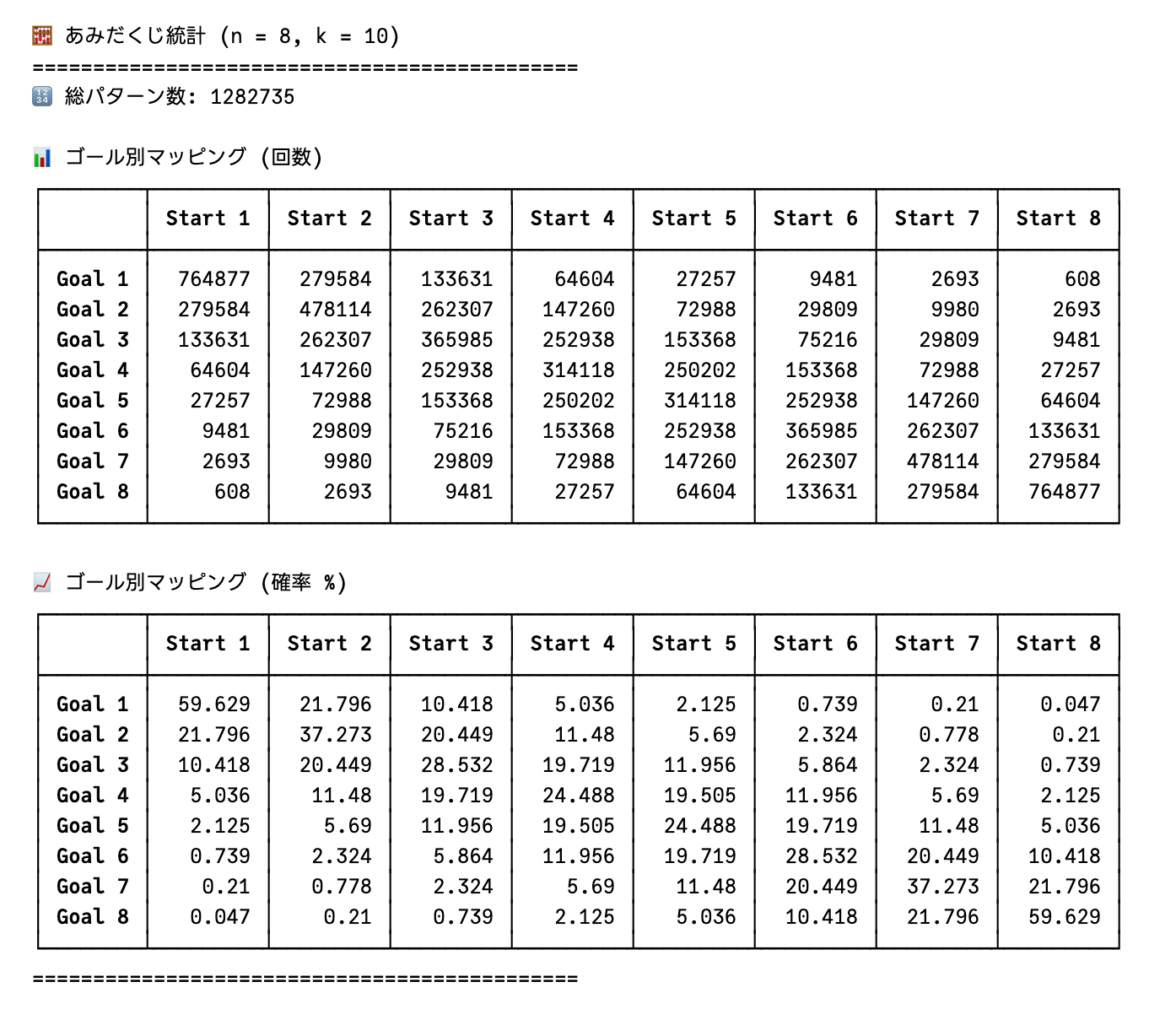
# 縦線8本，横線12本
calculate_amidakuji_distribution(8,12)
# 縦線10本，横線12本
calculate_amidakuji_distribution(10,12)

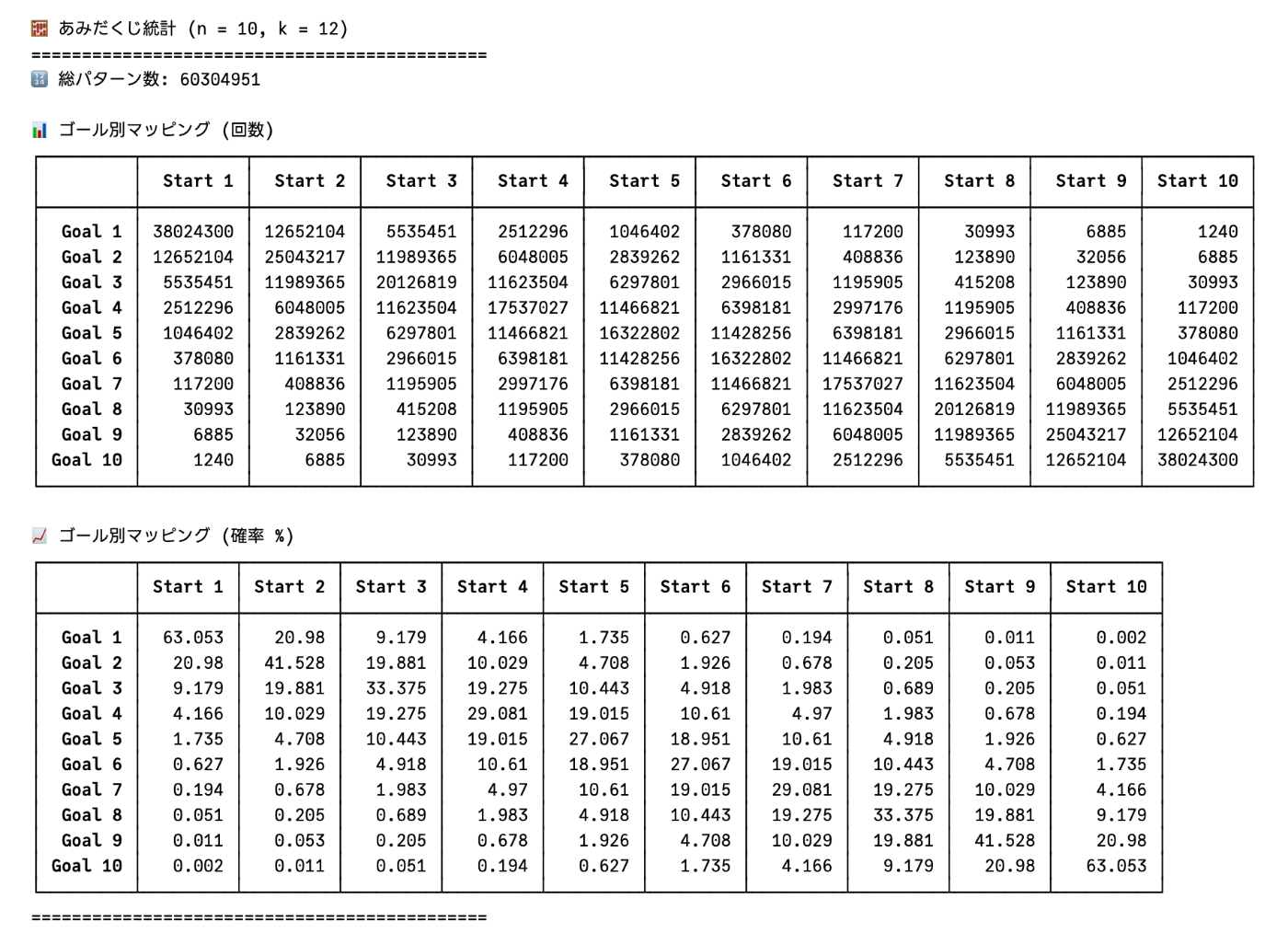
 コードの解説
 関数この関数calculate_amidakuji_distribution(tn, an)は，
✅ 縦の筋が tn本、

✅ 横線が an本ある、

あみだくじについて、

•	各スタート地点（1〜tn）が

•	最終的にどのゴール地点（1〜tn）にたどり着くか

•	その通り数（回数）と確率（%）
を計算し、表として表示するものです。

 計算の流れ次の順番で処理しています。

1.	DP（動的計画法）で、すべてのあみだくじパターンを数え上げる

2.	スタート地点→ゴール地点の移動結果を集計する

3.	結果を、回数と確率のテーブルにして出力する

 各ステップについて(1) 総ステップ数を決める
ln = 2*an + tn
•	あみだくじでは

•	「まっすぐ進む」ステップが tn

•	「戻る」動きは、横線1本で2ステップ（行きと戻り）必要

•	よって総ステップ数は\text{ln} = 2 \times an + tnで決まります。
(2) DPテーブル（状態管理用辞書）を初期化する
dp = Dict{Tuple{Int, Vector{Int}}, BigInt}()
dp[(0, collect(0:tn-1))] = 1
•	dpは、(現在の高さ, 現在の並び順) をキーにして

•	その状態に到達する通り数を記録する。

•	最初は

•	高さ=0

•	並び順=0,1,2,…,tn-1（つまり初期状態）

•	この初期状態は通り数1。
(3) ステップごとに動かす
for step in 1:ln-1
そのまま右に進む（+1）
if h + 1 <= tn - 1
    key_up = (h + 1, perm)
    new_dp[key_up] = get(new_dp, key_up, 0) + c
end
•	高さが1つ上がる

•	並び順（perm）は変わらない

•	通り数を引き継ぐ
横線で戻る（-1＋swap）
if h >= 1
    newh = h - 1
    perm2 = copy(perm)
    perm2[h], perm2[h+1] = perm2[h+1], perm2[h]
    key_dn = (newh, perm2)
    new_dp[key_dn] = get(new_dp, key_dn, 0) + c
end
•	高さが1つ下がる

•	隣の筋どうしをswapする

•	通り数を引き継ぐ
※ swapは「横線を引いて筋を入れ替えた」ことを意味する！
(4) 最後に結果をまとめる
for ((h, perm), c) in dp
    if h == tn - 1
•	最後のステップで高さが tn-1 にいるものだけ採用

•	ここから「最後の+1」をするとゴールに到達できる
ゴール別にカウント
for i in 1:tn
    stat[i, perm[i]+1] += c
end
•	stat[i, j]に、スタート位置j（1始まり）がゴール位置i（1始まり）に到達する通り数を足していく
(5) 出力する
総パターン数
println("🔢 総パターン数: $total")
回数テーブル
pretty_table(stat; header=..., row_labels=..., compact_printing=false)
•	スタート（横）、ゴール（縦） のきれいなテーブル
確率テーブル
percents = 100 .* stat ./ total
percents_float = Float64.(percents)
pretty_table(round.(percents_float; digits=3); header=..., row_labels=..., compact_printing=false)
•	パーセント表記

•	小数第3位まで丸める

 まとめ今回はDPを使って，高速化ができました。考えているテーブルも短時間で作成できました。

ただ，数学的なアプローチ，例えば，漸化式や母関数などが考慮できれば，違ったコードもできるのではないかと思います。@tsatieさん，楽しい題材をありがとうございました。

 1つの数式で求まるようですね下記のサイトで今回の話が議論されていることがわかりました。
http://shochandas.xsrv.jp/amida/amida.htm
このサイト見ていると，いわゆる「縦m本, 横線n本の標準的なあみだくじの総数の一般項」が行列を用いて表されていることに気がつきました。（DD＋＋さんのコメントです）
!
AmidakujiCountMatrix(m, n)= \mathbf{1}^\top \cdot A^{n-1} \cdot \mathbf{1}

\mathbf{1} は、長さ m-1 のすべての成分が1の列ベクトル

A は (m-1) \times (m-1) 行列で、その成分 A_{i,j} は次のように定義される：A_{i,j}=\begin{cases} 1 & \text{if} \quad i \ge j \quad \text{or} \quad i = j-1 \\ 0 & \text{otherwise} \end{cases}


 m=3のとき\left(\begin{matrix}
1 & 1
\end{matrix}\right)
\left(\begin{matrix}
1 & 1 \\
1 & 1 \\
\end{matrix}\right)^{n-1}
\left(\begin{matrix}
1 \\
1 \\
\end{matrix}\right)
 m=4のとき\left(\begin{matrix}
1 & 1 &1
\end{matrix}\right)
\left(\begin{matrix}
1 & 1 & 0\\
1 & 1 & 1 \\
1 & 1 & 1
\end{matrix}\right)^{n-1}
\left(\begin{matrix}
1 \\
1 \\
1
\end{matrix}\right)
 m=5のとき\left(\begin{matrix}
1 & 1 &1 &1
\end{matrix}\right)
\left(\begin{matrix}
1 & 1 & 0 & 0\\
1 & 1 & 1 & 0\\
1 & 1 & 1 & 1\\
1 & 1 & 1 & 1\\
\end{matrix}\right)^{n-1}
\left(\begin{matrix}
1 \\
1 \\
1 \\
1
\end{matrix}\right)
 m=6のとき\left(\begin{matrix}
1 & 1 &1 &1 &1
\end{matrix}\right)
\left(\begin{matrix}
1 & 1 & 0 & 0 &0\\
1 & 1 & 1 & 0&0\\
1 & 1 & 1 & 1&0\\
1 & 1 & 1 & 1&1\\
1 & 1 & 1 & 1&1\\
\end{matrix}\right)^{n-1}
\left(\begin{matrix}
1 \\
1 \\
1 \\
1 \\
1
\end{matrix}\right)
 Juliaのコードjulia言語への実装はこんな感じです。
amidakuji_count_matrix(m, n) = 
    ones(Int,m-1)' *
    [ (i >= j || i == j-1) ? 1 : 0 for i in 1:m-1, j in 1:m-1 ]^(n-1) *
    ones(Int,m-1)
せっかくなのでDataFrames.jlで綺麗に書いてみます。
using DataFrames
# 表を作る
m_range = 3:8   #縦棒の数
n_range = 1:20  #横棒の数

# 中身をためる
table = DataFrame(n = n_range)

for m in m_range
    values = [amidakuji_count_matrix(m, n) for n in n_range]
    table[!, "m=$m"] = values
end

# 表示
println(table)
これで，あみだくじはバッチリですね！

あみだくじの総数をJulia言語で求める。

はじめに

あみだくじの総数をどのように考えるのか？

あみだくじの総数の数え方

Julia言語によるコード化

コード

具体例

コードの解説

関数

計算の流れ

各ステップについて

まとめ

1つの数式で求まるようですね

$m=3$ のとき

$m=4$ のとき

$m=5$ のとき

$m=6$ のとき

Juliaのコード

Discussion