高校生が学習する仮説検定について,Juliaで調べてみる。
はじめに
高校1年生の数学Iの「データの分析」という単元の中で仮説検定について学習します。確率については数学Aで平行して学習するので,分布については具体的に与えることが多いです。数学Bの「統計的な推測」まで学習すると,二項分布など確率分布を与えることもできるようになります。数研出版の数学Ⅰの教科書には次のように書かれています。


仮説検定についてのTweet
まずは@Mathworld4さんのツイートからです。
今まで,正解率が70%で,今回は
「今回は頑張ったね。正答率上がったね!」
と,言ってあげたいのですが,このことを仮説検定に基づいて考えるということです。
仮説検定の流れ
対立仮説
この対立仮説が証明したい事柄になります。今回は「花子さんの学力が上がった」ということです。
帰無仮説
対立仮説に反対する仮説となります。すなわち,今回も「普段通りの正答率70%だった」ということとです。
有意水準
平たく言うと,今回起こった事柄「8問中7問題正解だった」は帰無仮説のもと考えると 「まあ,よくあること」なのか「レアケース」なのか を判断していきます。そのための判断基準が 有意水準5% となります。
今回,8問中7問題以上正解 であることが「まあ,よくあること」なのか「レアケース」なのかを確認していきますが,
- 8問中7問題以上正解する確率が0.05以上であれば,「まあ,よくあること」
- 8問中7問題以上正解する確率が0.05未満であれば,「レアケース」
と判断します。
仮説検定の結論
「まあ,よくあること」と判断した場合
この場合は,帰無仮説が否定されなかったので,「花子さんの学力が上がったどうかわからない」 と言う結論になります。注意点としては「花子さんの学力は上がっていない」と決めつけることはできないという点です。
「レアケース」と判断した場合
この場合は,帰無仮説が否定され,「花子さんの学力は上がった」 と判断します。
計算してみます。
実際に8問中7問題以上正解する確率を計算してみます。いつものようにjuliaで計算します。Distributions.jlのパッケージを使いました。
using Distributions
binomial(8,7)*(.7)^7*(.3)+(.7)^8
0.2552983299999999
よって,「まあ,よくあること」となり,「花子さんの学力が上がったどうかわからない」という結論になりました。
考察
@Mathworld4さんの解答のツイートをみると,8問中7問題正解するだけで,確率が0.05を超えてしまうことがわかりました。正解の割合ではないことには気がついていたので,どのくらい回数をこなせば,「学力が上がった」と判断できるのかが気になったので,調べてみることにしました。
実験
100問中80問正解した場合
まず,100問中80問正解した場合は「学力が上がった」と判断できるか調べてみました。有意水準は5%です。
100問中80問 以上 正解する確率は
p=0
n=100
k = 80
for i=k:n
p += binomial(BigInt(n),i)*(.7)^i*(.3)^(n-i)
end
println(p)
0.0164628532418693788358036977549403397060313662430586333319713050812319582425242
これは
ちなみに,100問中80問正解する確率は次の通りです。
p=0;n=100;k=80;i=k
binomial(BigInt(n),i)*(.7)^i*(.3)^(n-i)
0.007575644925726609797452082516340891794159647965788391922169648551623356549866915
100問中何問正解すると学力は上がるのか?
その境界を探ってみます!
function kentei(n)
p=0
for i=0:n
p += binomial(BigInt(n),i)*(.7)^(n-i)*(.3)^i
if p >= 0.05 && i==0
println("$(n)問中$(n-i)問正解しても学力は上がらない")
break
elseif p >= 0.05
println("$(n)問中$(n-i+1)問正解のとき学力は上がった。")
#println("学力は上がった。")
println("$(n)問中$(n-i)問正解のとき学力は上がったとはいえない。")
break
end
end
end
kentei(100)
100問中78問正解のとき学力は上がった。
100問中77問正解のとき学力は上がったとはいえない。
他の回数ではどうなるのか?
8問
kentei(8)
8問中8問正解しても学力は上がらない
9問
全問正解でも学力が上がったと判断できません。悲しい結果です。。。
kentei(9)
9問中9問正解のとき学力は上がった。
9問中8問正解のとき学力は上がったとはいえない。
20問
kentei(20)
20問中18問正解のとき学力は上がった。
20問中17問正解のとき学力は上がったとはいえない。
まとめて調べてみる
for i=10:10:100
kentei(i)
end
10問中10問正解のとき学力は上がった。
10問中9問正解のとき学力は上がったとはいえない。
20問中18問正解のとき学力は上がった。
20問中17問正解のとき学力は上がったとはいえない。
30問中26問正解のとき学力は上がった。
30問中25問正解のとき学力は上がったとはいえない。
40問中34問正解のとき学力は上がった。
40問中33問正解のとき学力は上がったとはいえない。
50問中41問正解のとき学力は上がった。
50問中40問正解のとき学力は上がったとはいえない。
60問中49問正解のとき学力は上がった。
60問中48問正解のとき学力は上がったとはいえない。
70問中56問正解のとき学力は上がった。
70問中55問正解のとき学力は上がったとはいえない。
80問中64問正解のとき学力は上がった。
80問中63問正解のとき学力は上がったとはいえない。
90問中71問正解のとき学力は上がった。
90問中70問正解のとき学力は上がったとはいえない。
100問中78問正解のとき学力は上がった。
100問中77問正解のとき学力は上がったとはいえない。
グラフ化
最後に
まず,データを準備します。
using DataFrames, GLM
# データを準備
y=[0];x=[0]
for n=9:50
push!(x,n::Int64)
push!(y,kentei2(n)::Int64)
end
deleteat!(x, 1)
deleteat!(y, 1);
data = DataFrame(X=x,Y=y)
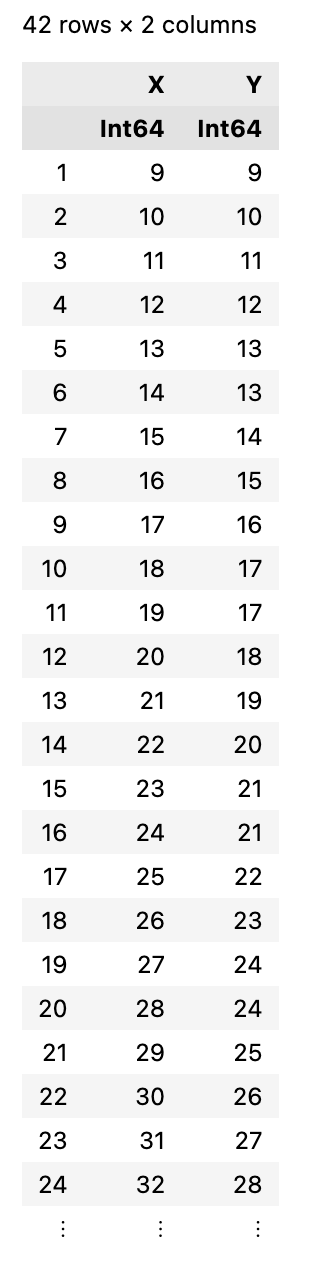
ols = lm(@formula(Y ~ X), data)

線形回帰は
グラフを見てみましょう!
using Plots
plot(x->2.63825+0.774167*x,xlim=(8,50),label=false)
scatter!(x,y,label=false)
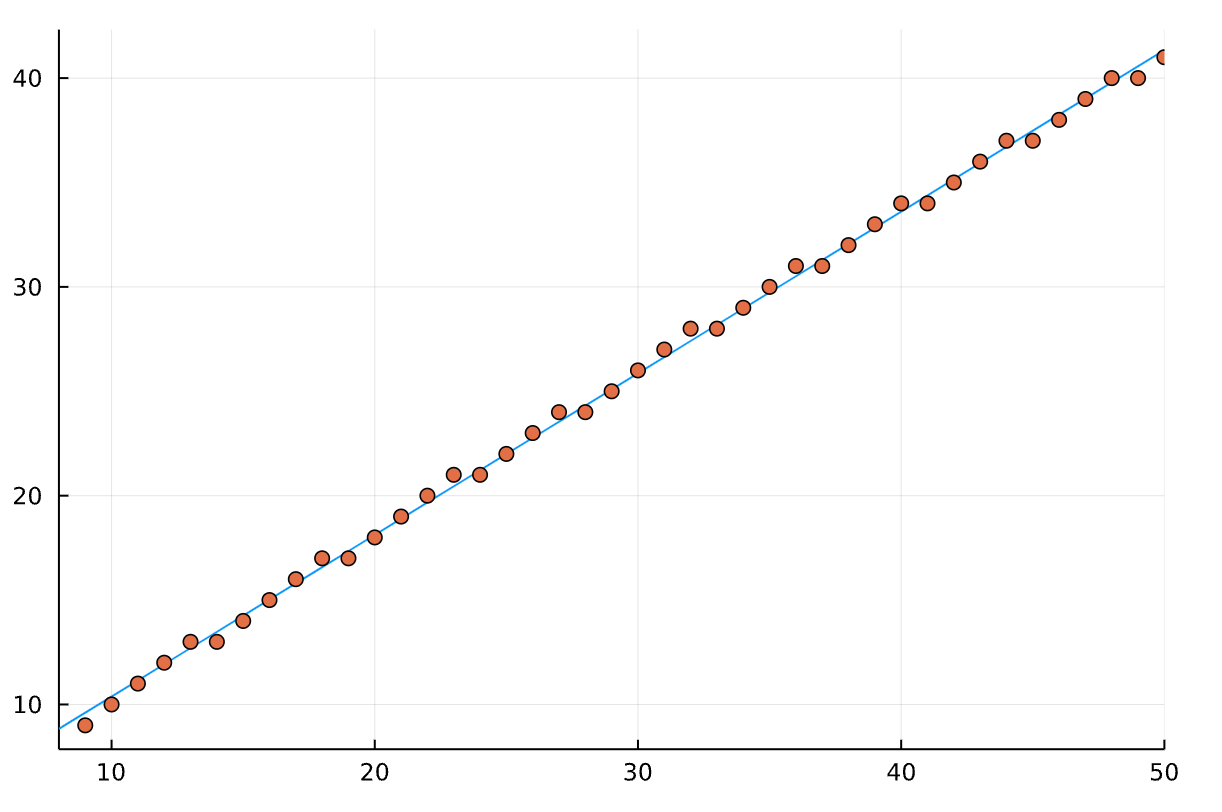
Discussion