正規分布X，Yの和X+Yについてjulia言語で考えてみた。

はじめに

Twitterから$\mathbb X$ に変わりました。$\mathbb X$での@TubeSolingさんのポストで，共通テストのような太郎くんと花子さんの会話文の統計の問題がありました。

https://twitter.com/TubeSoling/status/1698034594879250436

この，会話文の中で，

• 太郎：確かだけど、ある集団Aが2つの集団B，Cに分かれているとして，BとCが正規分布に従うんだったら A も正規分布に従うんじゃなかった？
• 花子：え？ そうなの？
• 太郎：あれ，違ったっけ？じゃあどうやって計算しよう？

とありました。「まあ，違うよな．．．」と思いながら，「どんな分布になるんだろう？」と思ったので，julia言語 を使って分布を書いてみることにしました。

日本人の身長の分布について

問題文で，太郎さんと花子さんの身長と，日本人の男女別の身長の平均と標準偏差が与えられています。そして，身長の分布は正規分布に従うそうです。

• 太郎くんの身長　168.6cm
• 花子さんの身長　185.4cm

太郎くんは私と同じくらいです。花子さんは高いですね。

	平均	標準偏差
日本人の男子	171.2cm	5.8cm
日本人の女子	158.2cm	5.2cm

まずは問題を解いてみます。

julia言語を用いて，問題を解いてみます。

第１問

1. 太郎さんより背が高い日本人女子と花子さんより背が高い日本人男子はどちらの方が多いか答えよ。

ポストでは正規分布表も与えられているのですが，ここはコマンドで求めてみます。Distributions.jlのパッケージを利用します。コマンドccdf(f,x)は分布fでx以上の確率を返します。

using Distributions # 分布パッケージ

ccdf(Normal(158.2,5.2),168.6)　 #　ccdf(f,x) f の分布で x 以上の確率を返す。

0.02275013194817915

太郎さんより身長が高い日本人女子は2.27%。100人中2人くらいしかいませんね。

ccdf(Normal(171.2,5.8),185.4) 

0.007177085392942717

花子さんより身長が高い日本人男子は0.71%。100人中1人もいません。

次のような結論になります。

日本人女子と日本人男子が同数とすると，太郎さんより身長の高い日本人女子の方が，花子さんより身長の高い日本人男子よりも多い。

第２問

2. 太郎さんの発言「ある集団Aが2つの集団B, Cに分かれているとして，BとCが正規分布に従うんだったらAも正規分布に従う」は一般に正しいか。理由も込みで述べよ。

このことを考える前に，正規分布について成り立つ性質があります。

$X$，$Y$を独立な正規分布で，$X\sim N(\mu_x,\sigma_x^2)$，$Y\sim N(\mu_y,\sigma_y^2)$とする。

$Z=X+Y$とすると，$Z\sim N(\mu_x+\mu_y,\sigma_x^2+\sigma_y^2)$である。

この性質は正規分布の再生性と呼ばれ，多くのサイトで説明があります。

https://bellcurve.jp/statistics/course/7799.html

「今回はこの性質なのかな？」と考えてみると，ちょっと違うことがわかります。まず，集団Aの平均は集団BとCの平均をそれぞれ加えたものではありません。おそらく男女同数であれば，Aの平均は2で割る必要があると思われます。

今回の分布は2つの正規分布を1:1で混ぜた混合ガウス分布（GMM） となります。確率密度関数それぞれ，0.5倍して加えます。

https://mathwords.net/gmm

これらのグラフをStatsPlots.jlパッケージを使って書いてみます。

plot.jl

using StatsPlots

X = Normal(171.2,5.8) # 日本人男子の分布（正規分布）
Y = Normal(158.2,5.2) # 日本人女子の分布（正規分布）
Z = Normal(158.2+171.2,√(5.8^2+5.2^2)) # X+Yの分布
G = MixtureModel([X,Y],[.5,.5])# 混合ガウス分布 X:Y = 1:1

plot(X,label="JPN men")
plot!(Y,label="JPN women")
plot!(Z,label="X+Y")
plot!(x->pdf(G,x),label="GMM")

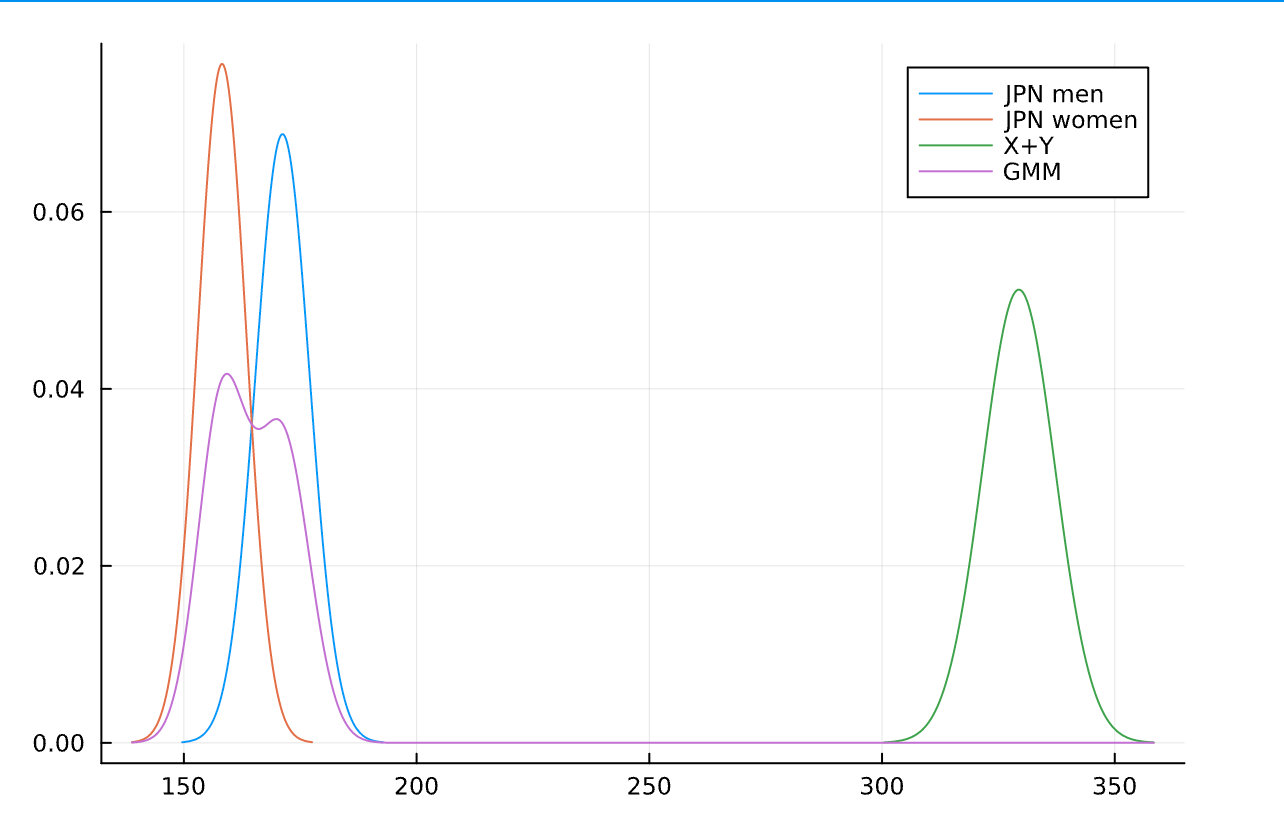
第3問

3. 花子さんは日本人全体で見れば上位何パーセントの身長か、小数第3位まで計算せよ。

混合ガウス分布を利用して，求めてみます。

ccdf(G,185.4)*100

0.3588584898003955

花子さんは上位0.358%であることがわかります。

これは男女別に調べてもわかります。

a = ccdf(X,185.4)*100

0.7177085392942717

b = ccdf(Y,185.4)*100

8.440306529671548e-6

(a+b)/2

0.3588584898004007

同じ結果ですね。

正規分布表を用いて手計算で解いてみる。

第１問

$Z_y=\dfrac{Y-158.2}{5.2}$とおくと，$Z\sim N(0,1)$となる。

$Y\geqq 168.6$とすると，

$Z_y\geqq {168.6-158.2}{5.2}=\dfrac{10.4}{5.2}=2$

$P(Z_y\geqq 2)=1-P(Z_y\leqq 2)=0.5-0.4772=0.0228$

太郎さんより身長が高い日本人女子は2.28%。

$Z_x=\dfrac{X-171.2}{5.8}$とおくと，$Z\sim N(0,1)$となる。

$X\geqq 185.4$とすると，

$Z_x\geqq {185.4-171.2}{5.8}=\dfrac{14.2}{5.8}=2.448\approx2.45$

$P(Z_x\geqq 2.45)=1-P(Z_x\leqq 2)=0.5-0.4929=0.0071$

花子さんより身長が高い日本人男子は0.71%。

第2問

一般的に正しくない。分布は一般に混合ガウス分布となり，正規分布とは異なる。

第３問

$Z_y=\dfrac{Y-158.2}{5.2}$とおくと，$Z\sim N(0,1)$となる。

$Y\geqq 185.4$とすると，

$Z_y\geqq {185.4-158.2}{5.2}=\dfrac{27.2}{5.2}=5.230\approx5.23$

正規分布表は3.09までしかないですね。$P(Z_y\geqq 5.23)=0$とします。

よって，$\dfrac{0.0071+0}{2}\times 100=0.355（％）$

花子さんは上位0.355%であることがわかります。

データで確認してみる。

• 男子1,000,000人，女子1,000,000人を正規乱数を用いてヒストグラムを作成。
• 正規乱数で作成した男子1,000,000人，女子1,000,000人を混ぜて，GMMのヒストグラムを作成。
• 正規乱数で作成した男子1000人(X)，女子1000人(Y)より，X+Y（データ数1,000,000）のヒストグラムを作成。

using StatsPlots,Distributions

function graph(n)
    p = map(x->(5.8*x+171.2),randn(10^(2*n))) # 日本男子10^n人
    q = map(x->(5.2*x+158.2),randn(10^(2*n))) # 日本女子10^n人

    l=[] # GMM
    for i=1:Int(10^(2*n))
        append!(l,p[i])
        append!(l,q[i]) 
    end

    k=[] # X+Y
    for i=1:10^n,j=1:10^n
        append!(k,p[i]+q[j])
    end
    
    # ヒストグラム
    histogram(p,alpha=0.1,label="mem")
    histogram!(q,alpha=0.1,label="womem")
    histogram!(l,alpha=1,label="GMM")
    histogram!(k,alpha=0.1,label="X+Y")
end

graph(3)

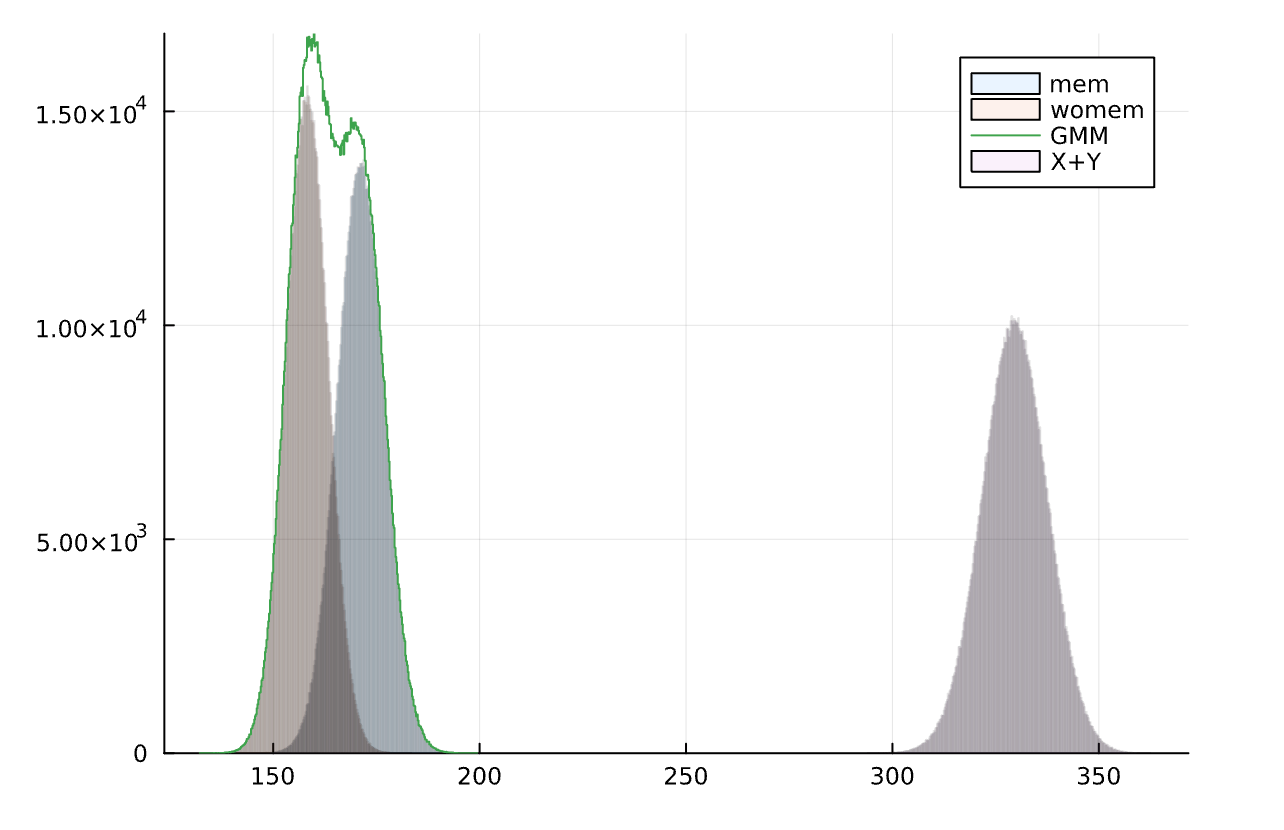
X+Yの分布を除いてみてみます。

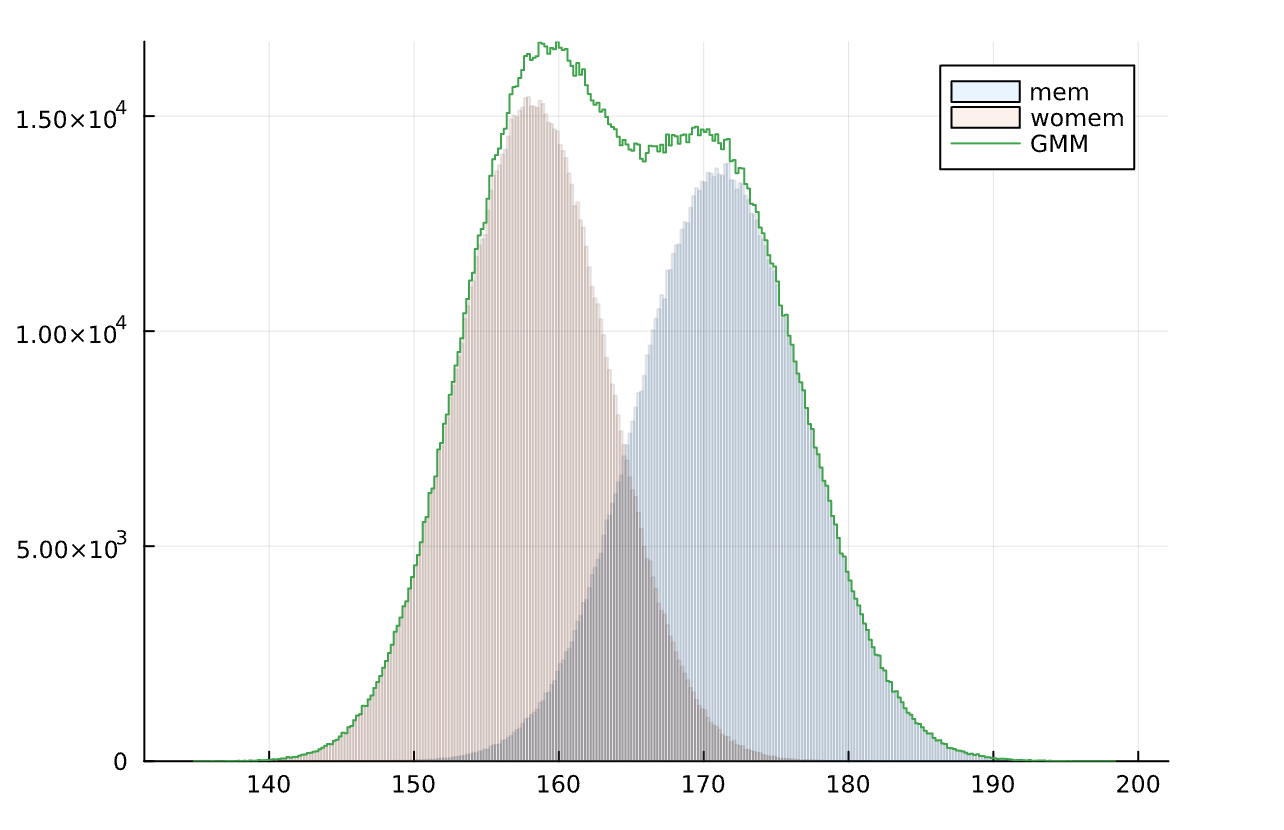
やはり，正規分布ではないですね。