ゼロから始める勾配ブースティング決定木の理論

はじめに

はじめまして。データアナリティクスラボの力岡です。
私は日頃、テーブルデータの分析業務において、LightGBMをはじめとする勾配ブースティング系アルゴリズムを活用しています。ただし、その仕組みを十分に理解したうえで使いこなせているかというと、まだ自信が持てない部分もあります。そこで本記事では、自分自身の理解を深めるとともに、これから学ぶ方々にも役立つよう、勾配ブースティング決定木（GBDT）について体系的に解説していきます。

1. 勾配ブースティング決定木

勾配ブースティング決定木（Gradient Boosting Decision Trees、GBDT） は、複数の決定木（弱学習器）を組み合わせて高い予測精度を実現する、アンサンブル学習の一手法です。その名の通り、「勾配降下法」「ブースティング」「決定木」という3つの要素を組み合わせて構成されており、実務やKaggleなどのデータ分析コンペでも非常に人気があります。

本章ではまずGBDTの全体像を紹介し、次章以降でその各構成要素について詳しく解説していきます。

1.1 GBDTを構成する3つの要素

• 勾配降下法（Gradient Descent）
  モデルの誤差（損失関数）を最小化するために、パラメータや予測関数を少しずつ調整していく最適化手法です。GBDTでは、現在の予測と正解との差（残差）を勾配とみなし、次の決定木がその残差を学習することで、モデル全体を改善していきます。ここでは、明示的なパラメータ更新ではなく、「予測関数そのもの」を勾配方向に改善していくという形で、関数空間における勾配降下法が用いられます。

• ブースティング（Boosting）
  性能の低い複数の弱学習器を順番に学習させ、それぞれの誤りを次の学習器が補うことで、全体として高性能なモデルを構築するアンサンブル手法です。GBDTでは、新しい決定木を逐次追加し、前の木が取りこぼした残差を段階的に補正していきます。

• 決定木（Decision Tree）
  特徴量に基づいてデータを条件分岐し、最終的に予測値を出力するツリー構造のモデルです。GBDTでは、一般的に浅い決定木を多数組み合わせることで、過学習を抑えつつ高い予測性能を実現します。

1.2 GBDTの長所と短所

GBDTはさまざまなタスクに適用可能な汎用性の高い手法ですが、他のアルゴリズムと同様にメリットとデメリットがあります。

メリット

• 高い予測精度を実現し、実務においても信頼性が高い。
• 特徴量のスケーリングや外れ値処理が不要で、前処理が比較的容易。
• 回帰・分類の両タスクに対応可能。
• 欠損値を自動で扱える実装も多い（例：XGBoost、LightGBM）。

デメリット

• モデルの構築に時間がかかりやすく、大規模データでは計算コストが高い。
• 弱学習器を順番に学習させるため、並列処理が困難。
• ハイパーパラメータの調整が多く、チューニングが煩雑。
• モデル構造が複雑で、単一の決定木と比べて可視化・解釈が難しい。

1.3 GBDTの歴史と発展

GBDTの原型となるアイデアは1990年代に登場し、以降、アルゴリズムの改良や実装の最適化が進められてきました。近年では、処理速度の向上、メモリ使用量の削減、カテゴリ変数への対応強化など、実務的なニーズに応える形での発展が続いています。

以下は、GBDTに関連する主要な技術的進展をまとめた年表です。

年	アルゴリズム	概要
1995	AdaBoost (Freund & Schapire)	誤分類サンプルへの重み付けを用いたブースティングを提案。​
1999	Gradient Boosting (Friedman)	関数空間における勾配降下法を用いた逐次最適化アルゴリズムを提案。
2014	XGBoost (Chen)	ヒストグラム分割、並列学習、欠損値処理などによる高速かつ精度の高い実装を公開。
2016	LightGBM (Microsoft)	Leaf-wise成長戦略、GOSS、EFBなどにより高速化と省メモリ化を実現。
2017	CatBoost (Yandex)	Ordered Boostingおよび順序保存型ターゲットエンコーディングにより、カテゴリ変数への強力な対応を実現。

2. 決定木

決定木（Decision Tree） は、特徴量に基づいてデータを条件分岐させ、分類や回帰を行う機械学習モデルです。構造は「木」のような形をしており、各分岐点（ノード）で条件判断を繰り返しながら、最終的な予測値にたどり着きます。

視覚的にわかりやすく、特徴量の重要性や規則性も直感的に理解できるため、解釈性の高いモデルとして広く利用されています。

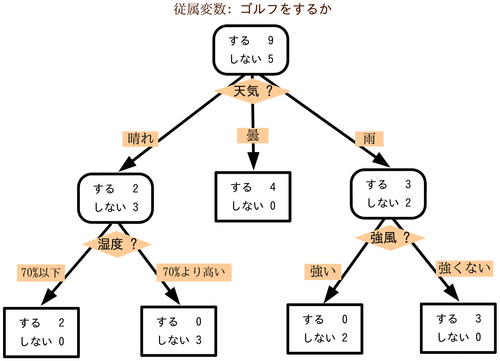
決定木のイメージ　出典：https://ja.wikipedia.org/wiki/決定木

決定木に関する詳しい解説は以下の記事でも紹介していますので、興味がある方はぜひご覧ください。
https://dalab.jp/mag/methods/decision-tree-analysis/

2.1 決定木の構造と用語

決定木を理解するには、まずその基本構造と用語を押さえることが重要です。

• 根ノード（root node）：すべてのデータを保持し、最初の分岐が行われるノード
• 親ノード（parent node）：子ノードを持つノード
• 子ノード（child node）：親ノードの条件分岐によって生成されるノード
• 葉ノード（leaf node）：それ以上分岐せず、最終的な予測や分類結果を出力するノード

データは根ノードから出発して、各ノードの条件に応じて再帰的に分岐され、最終的に葉ノードへ到達します。葉ノードでは、分類であれば最も多いクラス、回帰であれば平均値などが予測結果として出力されます。

決定木の構造　出典：https://zero2one.jp/ai-word/decision-tree/

2.2 CART

決定木にはさまざまなアルゴリズムがありますが、最も一般的かつ広く使われているのが、CART（Classification And Regression Tree） です。CARTは、分類・回帰の両方に対応でき、scikit-learnなど多くの機械学習ライブラリで標準的に実装されています。

【CARTの主な特徴】

• 二分木構造：常に2つの子ノードに分割する二分木を生成する。​
• 分割基準：各分割では、ノード内のデータができるだけ同じクラスや値で構成されるように、最も整った（＝不純度が小さくなる）分割条件を選ぶ。
• 再帰的分割：各ノードで最適な特徴量と分割点を選び、データを再帰的に分割して木を構築する。​
• 剪定（Pruning）：生成された木はそのままでは過学習を起こしやすいため、後処理として剪定を行い、汎化性能を高める。

CARTのイメージ　出典：https://dalab.jp/mag/methods/decision-tree-analysis/

項目	説明
petal length (cm) <= 2.45	​分岐の条件（特徴量と閾値）
gini = 0.667	​ジニ不純度
samples = 120	​ノード内のサンプル数
value = [40, 41, 39]	​各クラスのサンプル数
class = versicolor	​最も多いクラス（分類結果）

不純度

不純度 とは、ノード内のデータがどれだけ混ざっているかを数値で表す指標です。不純度が低いほど、データが特定のクラスや値に偏っている（＝純粋である）とみなされます。

分類と回帰では、それぞれ異なる指標が使われます。

• 分類の不純度指標
  代表的な指標として、ジニ不純度（Gini impurity） やエントロピー（Entropy） が用いられます。これらはノード内のクラスの混在度合いを測る指標で、値が0に近いほど特定のクラスに偏っていることを意味します。
• 回帰の不純度指標
  代表的な指標として、平均二乗誤差（MSE） や平均絶対誤差（MAE） が用いられます。これらはノード内の目的変数の値がどれだけ散らばっているか（＝予測と実際の値とのズレ）を示します。

CARTでは、ノードの不純度が最も小さくなるように分割を繰り返していきます。

ジニ不純度について

ジニ不純度（Gini impurity） は、あるノードに含まれるデータが複数クラスにどれだけ混在しているかを示す指標です。

$$Gini(D) = 1 - \sum_{i=1}^K p_i^2$$

• $D$: ノードに含まれるデータ集合
• $K$: クラス数
• $p_i$: $D$ におけるクラス $i$ の出現確率

すべてのデータが同一クラスであれば $Gini = 0$ となり、最も純粋な状態を表しています。

剪定

決定木は柔軟なモデルである一方、すべての訓練データに対応しようとすると、木が必要以上に深くなり、過学習（overfitting） を引き起こすリスクがあります。これは、訓練データに対しては高い精度を示す一方で、新しいデータ（未知データ）に対する予測精度が低下し、汎化性能が低くなる状態です。

この問題を防ぐために、剪定（Pruning） という手法が用いられます。剪定とは、予測に貢献しない枝を削除して、モデルをよりシンプルにすることです。これにより、モデルの過剰な複雑さを抑え、汎化性能の向上が期待できます。

CARTでは、剪定方法としてコスト複雑度剪定（Cost-Complexity Pruning） が標準的に採用されています。まず、可能な限り成長させた大きな木を構築し、その後、コスト複雑度剪定を通じて不要な枝を削除することで、適度な複雑さと精度のバランスが取れた決定木に調整します。

コスト複雑度剪定について

コスト複雑度剪定（Cost-Complexity Pruning） 、誤差とモデルの複雑さのバランスを取ることで、過学習を防ぐ剪定手法です。以下の目的関数を最小化します。

$$R_\alpha(T) = R(T) + \alpha \cdot |T|$$

• $R(T)$: 決定木 $T$ の誤差（例：分類誤差、MSEなど）
• $|T|$: 葉ノードの数（木の複雑さ）
• $\alpha$: 複雑さに対するペナルティを調整する正則化パラメータ

$\alpha$ の値を調整することで、より複雑な木（誤差は小さいが過学習しやすい）と、よりシンプルな木（誤差は多少大きくても汎化しやすい）のバランスを取ることができます。

3. アンサンブル学習

アンサンブル学習（Ensemble Learning） とは、複数の機械学習モデルを組み合わせることで、単一モデルよりも高い予測精度や汎化性能を実現する手法です。モデル同士が互いの弱点を補完し合うことで、過学習を抑えつつ、安定した性能を得られるのが大きな特長です。

3.1 アンサンブル学習の代表的な手法

アンサンブル学習には、主に以下の3つのアプローチがあります。それぞれ異なる仕組みで精度向上を目指します。

手法	代表モデル	アプローチの特徴	主な改善対象
バギング（Bagging）	ランダムフォレスト	複数のモデルを並列に学習し、予測を平均または多数決で統合	分散（Variance）
ブースティング（Boosting）	AdaBoost、Gradient Boosting	モデルを逐次的に学習し、前の誤りを後のモデルで補正	バイアス（Bias）
スタッキング（Stacking）	Stacked Generalization	異なるモデルの出力をメタモデルで再学習して統合	バイアス&分散

それぞれの手法の詳細について、以下で解説します。

3.2 バギング

バギング（Bagging：Bootstrap Aggregating） は、同じアルゴリズムを用いて複数のモデルを並列に学習させ、その予測結果を平均（回帰）または多数決（分類）で統合する手法です。

特徴は、訓練データから復元抽出（ブートストラップ） によって複数のサブデータセットを作成する点です。各モデルは異なるサブセットで独立に学習されるため、過学習を抑えながら精度と安定性を向上させられます。

ランダムフォレスト

ランダムフォレストは、バギングを決定木に適用した代表的な手法で、さらに特徴量のランダム選択を取り入れることで、モデル同士の相関を減らし、多様性を高めています。

【ランダムフォレストの基本フロー】

1. データのサンプリング（ブートストラップ）
   元の訓練データからランダムにレコード（行）を抽出し、複数のサブデータセットを生成。
2. 特徴量のランダム選択
   各決定木の分岐時に、使用する特徴量（列）をランダムに選択して多様性を確保。
3. 複数モデルの統合
   学習済みの決定木の予測を、分類では多数決、回帰では平均で統合。

このように、「データの多様性」と「モデルの多様性」を活かすことで、高い汎化性能を実現できるのがランダムフォレストの強みです。

ランダムフォレストの学習　出典：https://note.com/shuwasystem/n/n0241f8ed81c2

3.3 ブースティング

ブースティング（Boosting） は、弱学習器を直列に学習させていくことで、全体として高精度な予測モデルを構築する手法です。

この手法のポイントは、「前のモデルが苦手としたデータを、次のモデルが重点的に学習する」という点にあります。モデルを1つずつ積み重ねることで、段階的に誤差を修正し、予測性能を向上させていきます。

バギングとの違い

バギングは並列学習であり、主にモデルの分散を抑えるのが目的でしたが、ブースティングは逐次学習によってバイアス（予測のずれ）を削っていく手法です。

項目	バギング	ブースティング
学習方式	並列	逐次（直列）
主な目的	分散の低減	バイアスの低減
データの使い方	各モデルに異なるサブセット	同じデータを使って誤差を順に修正
精度の改善手段	予測の平均・多数決	残差の加算的修正

ブースティングは、データが少ない場合や複雑な関係がある場合に特に有効で、高い精度が得られることが多い手法です。

勾配ブースティング

勾配ブースティング（Gradient Boosting） は、ブースティング手法の一種で、損失関数の勾配情報を用いて残差を削減していくのが特徴です。現在の残差を、新しいモデルが予測することで、段階的に性能を高めていきます。

【勾配ブースティングの基本フロー】

1. 初期モデルで平均などのシンプルな予測を行う。
2. 残差を新たな目的変数として、次のモデルを学習。
3. 学習したモデルの出力を加算し、全体の予測を更新。
4. このプロセスを繰り返し、段階的に精度を向上。

この手法に基づいた代表的なアルゴリズムには、XGBoost、LightGBM、CatBoostなどがあります（詳細は後述）。

勾配ブースティングの学習　出典：https://note.com/shuwasystem/n/n0241f8ed81c2

3.4 スタッキング

スタッキング（Stacking） は、複数の異なるモデルの予測結果を組み合わせ、それらを新たな入力としてメタモデル で最終予測を行う手法です。

ブースティングやバギングが同一アルゴリズムを用いるのに対し、スタッキングは異なるアルゴリズム（例：ロジスティック回帰、ランダムフォレスト、SVMなど）を組み合わせることが多い点が特徴です。

【スタッキングの構成】

• 第1層（ベースモデル）
  複数の異なるモデルを訓練データで学習し、それぞれが出した予測結果を新たな特徴量として扱う。
• 第2層（メタモデル）
  第1層のモデルの出力を入力とし、それを元に最終的な予測を行う。

このように、複数のモデルの強みをうまく融合することで、個々のモデルを超える性能を実現することが期待されます。ただし、構成が複雑になりやすく、クロスバリデーションやハイパーパラメータ調整などの慎重な設計が求められます。

スタッキングの学習　出典：https://datawokagaku.com/ensemble/

4. 勾配降下法

勾配降下法（Gradient Descent） は、機械学習において最も基本かつ重要な最適化アルゴリズムのひとつです。モデルの損失関数を最小化するために、その勾配（偏微分）に沿ってパラメータを少しずつ更新していきます。

GBDTでは、この勾配降下法を関数空間上に拡張することで、複雑な関数を段階的に近似していきます。

4.1 勾配降下法の基本

勾配降下法は、損失関数を最小化するために、パラメータを少しずつ更新する手法です。現在の予測結果に対する誤差の傾きを計算し、その逆方向にパラメータを移動させることで、徐々に最適な値に近づいていきます。

勾配とは
勾配とは、損失関数を各パラメータで偏微分した値であり、「損失が最も急激に増加する向き」を示します。勾配の逆向きに進むことで、効率的に損失を減らすことができます。

損失関数 $\mathcal{L}(\boldsymbol{\theta})$ に対する勾配ベクトル $\nabla \mathcal{L}(\boldsymbol{\theta})$ は、次のように定義されます。

$$\nabla \mathcal{L}(\boldsymbol{\theta}) = \left( \frac{\partial \mathcal{L}}{\partial \theta_1},\ \frac{\partial \mathcal{L}}{\partial \theta_2},\ \dots,\ \frac{\partial \mathcal{L}}{\partial \theta_n} \right)$$

ここで $\boldsymbol{\theta} = (\theta_1, \theta_2, \dots, \theta_n)$ はモデルのパラメータのベクトルです。各偏微分項は、対応するパラメータが損失関数に与える影響を示しています。

【勾配降下法の基本フロー】

1. パラメータの初期値を設定する。
2. 現在のパラメータにおける損失関数の勾配を計算する。
3. 勾配の逆方向にパラメータを更新する。
4. 損失関数の変化が小さくなるまで、2〜3を繰り返す。

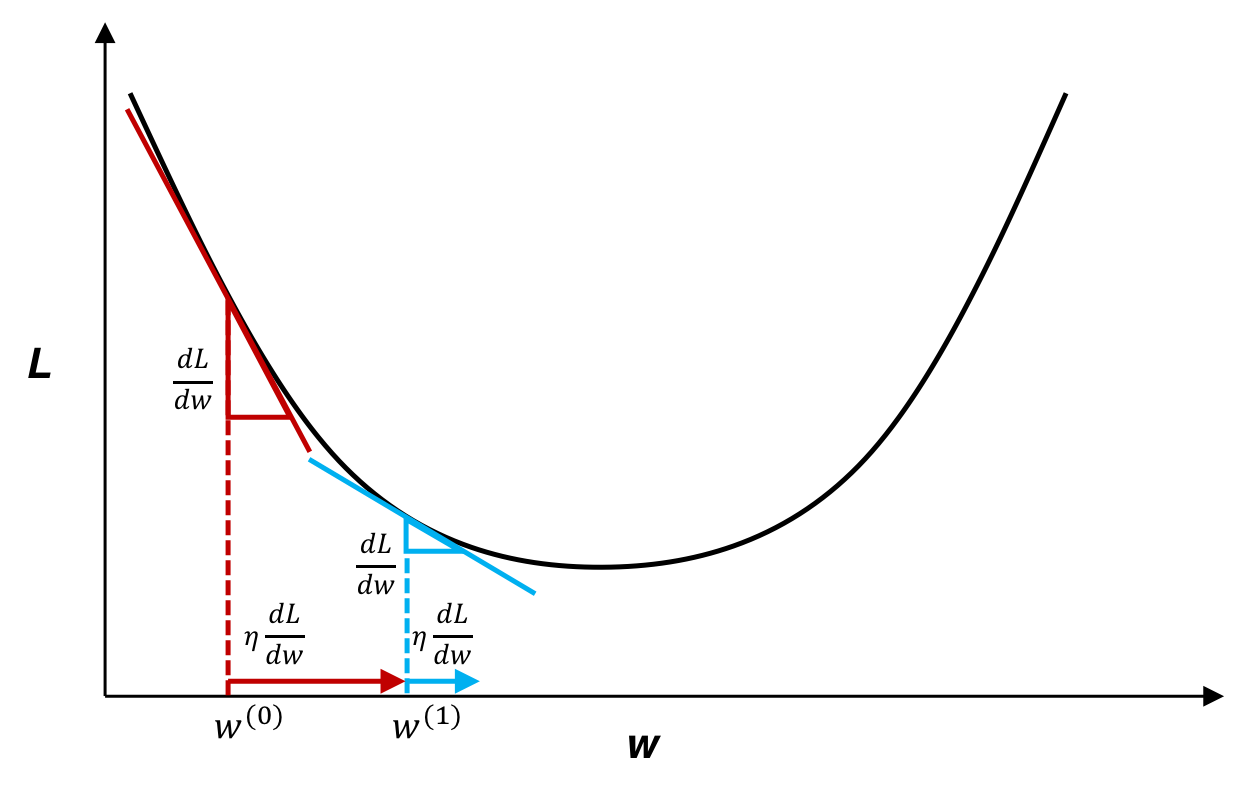
勾配降下法　出典：https://axa.biopapyrus.jp/deep-learning/gradient_descent_method.html

勾配降下法は、回帰分析やニューラルネットワークを含む多くの機械学習アルゴリズムの核となっています。そして、この考え方を 「関数そのもの」に適用したのがGBDTの発想です。

4.2 関数空間での勾配降下法

GBDTでは、通常のようにパラメータを直接最適化するのではなく、予測関数そのものを改善していくアプローチを取ります。これは「関数空間における勾配降下法」と呼ばれ、各ステップでモデルを少しずつ更新していきます。

【弱学習器による関数の更新】

$m$ 本目の弱学習器を追加する際には、1つ前のモデル $F_{m-1}(x)$ に対して、損失関数の負の勾配を以下のように計算します。
 

$$g_{im} = -\left. \frac{\partial \mathcal{L}(y_i, F(x_i))}{\partial F(x_i)} \right|_{F(x) = F_{m-1}(x)}$$

 
この勾配 $g_{im}$ は、現在の予測が正解からどれだけズレているか、そしてどの方向に補正すべきかを示します。これを新たな目的変数として扱い、弱学習器 $h_m(x)$（一般に浅い決定木）を学習させます。

【モデルの更新式】

学習した弱学習器 $h_m(x)$ の出力を、予測に加算してモデルを更新します。
 

$$F_m(x) = F_{m-1}(x) + \nu \cdot h_m(x)$$

• $F_m(x)$：$m$本目までの累積予測関数
• $\nu$：学習率（learning rate）
• $h_m(x)$：負の勾配を近似する弱学習器

このようにして、モデルを段階的に改善していくのがGBDTの基本的な仕組みです。

4.3 アディティブモデルとステージワイズ最適化

GBDTのモデル全体は、次のようなアディティブモデル（加法モデル） で表現されます。
 

$$F_M(x) = \sum_{m=1}^M \nu \cdot h_m(x)$$

 
ここで重要なのは、「すべてのモデルを一度に学習するのではなく、1本ずつ弱学習器を追加していく」という点です。これをステージワイズ最適化と呼びます。この逐次的な学習戦略により、柔軟に誤差を修正しながら、全体の損失を段階的に減らしていくことが可能になります。

🔧 学習率 $\nu$ の役割

学習率 $\nu \in (0, 1]$ は、1回の更新でどれだけモデルを修正するかを決める重要なパラメータです。

学習率 $\nu$	特徴
小さい（例：0.01〜0.3）	学習はゆっくりだが過学習しにくく、汎化性能が高い。
大きい（例：0.5〜1.0）	収束が速いが過学習しやすく、不安定になることもある。

学習率が小さいほど、より多くの弱学習器を積み重ねる必要がありますが、予測精度の向上と過学習の抑制が期待できます。

5. GBDTアルゴリズムの詳細

ここでは、これまで解説してきたGBDTの基本概念をもとに、実際のアルゴリズムの流れや重要なパラメータについて掘り下げていきます。

5.1 学習ステップ

GBDTの学習は、以下のようなステップで構成されます。

【GBDTの基本的な反復手順】

1. 初期予測の設定
   まず初期予測関数 $F_0(x)$ を定義します。
   • 回帰の場合：目的変数 $y$ の平均値を使用
   • 分類の場合：クラスの事前確率（例：logit関数）を使用
2. 負の勾配（残差）の計算
   各サンプル $i$ に対して、現在のモデル $F_{m-1}(x)$ における損失関数の勾配を計算します。

$$g_{im} = -\left. \frac{\partial \mathcal{L}(y_i, F(x_i))}{\partial F(x_i)} \right|_{F(x) = F_{m-1}(x)}$$

4. 弱学習器の学習
   残差 $g_{im}$ を目的変数として、決定木 $h_m(x)$ を学習します。
   ここで得られる $h_m(x)$ は、誤差を補正する方向を表す関数です。
5. モデルの更新
   学習した弱学習器を使って、予測関数を更新します。

$$F_m(x) = F_{m-1}(x) + \nu \cdot h_m(x)$$

5. 次のステップへ進む
   上記ステップを $m = 1$ から $M$ まで繰り返し、最終モデル $F_M(x)$ を得ます。

5.2 パラメータの役割

GBDTでは多くのハイパーパラメータがあり、モデル性能に大きく影響します。代表的なものを以下に整理します。

パラメータ	説明
learning_rate	各木の寄与を抑える係数。小さいほど安定だが学習に時間がかかる（=より多くの木が必要）
n_estimators	使用する決定木の本数。多いほど精度向上しやすいが過学習にも注意
max_depth / num_leaves	決定木の深さ／葉の数の上限。高くすると複雑なルールが学習できるが過学習しやすくなる
subsample	各学習ステップで使用するデータの割合（例：0.8 → 80%使用）。過学習の抑制に有効
colsample_bytree	決定木1本あたりに使う特徴量の割合。特徴量の多いデータで有効
min_child_weight / min_data_in_leaf	葉ノードに含める最小の重みまたはサンプル数。小さいと木が複雑になりやすい
lambda_l1 / lambda_l2	L1/L2正則化項。モデルの複雑さにペナルティを加えることで過学習を抑制

6. 主要ライブラリ比較

GBDTにはさまざまな実装ライブラリが存在し、それぞれが独自の工夫により、性能・精度・使い勝手を高めています。本章では、代表的な3つのライブラリ XGBoost, LightGBM, CatBoost を比較し、それぞれの構造・最適化技術・欠損値処理などを解説します。

ライブラリ比較表

比較観点	XGBoost	LightGBM	CatBoost
木構造戦略	Level-wise（層ごとに分割）	Leaf-wise（利得が最大の葉を優先的に分割）	Oblivious Tree（各レベルで同一分割）
カテゴリ変数処理	One-hot / target encoding	One-hot / 自動的に分割点を最適化	順序付きターゲットエンコーディング
欠損値処理	分割方向を最適化して自動処理	分割探索中に欠損の最適方向を同時に学習	欠損値をカテゴリとして扱い自動処理
対応タスク	回帰・分類・ランキング	回帰・分類・ランキング・多クラス	回帰・分類・ランキング
スケーラビリティ	◯（中〜大規模）	◎（億レコード級）	◯（中規模向け）

ライブラリ選択早見表

こんな時は…	おすすめライブラリ	理由
億レコード級を高速に学習	LightGBM	Leaf‑wise+GOSSによる学習高速化、GPU&分散が強力
カテゴリ変数が多く前処理を減らしたい	CatBoost	順序付きターゲットエンコーディングでデータリークを防ぎつつ自動前処理
オプションが豊富で王道を選びたい	XGBoost	正則化・DART など多彩な設定で幅広いケースに対応
推論レイテンシ重視 (オンライン)	CatBoost	対称木で高速推論・モデルサイズも比較的コンパクト
CPU 環境・中規模データで堅実に	XGBoost	GPUなしでも安定した精度と速度

各ライブラリにおける木構造の比較図　出典：https://medium.com/riskified-technology/xgboost-lightgbm-or-catboost-which-boosting-algorithm-should-i-use-e7fda7bb36bc

また、主要なGBDT系ライブラリは、欠損値を自動で処理できる機能を備えています。これは、欠損値を事前に補完しなくても学習・推論ができるという点で非常に便利です。

6.1 XGBoost

XGBoostは、2016年にTianqi Chenらによって発表されたGBDTの高性能実装であり、Kaggleや実務で非常に広く使われています。

https://arxiv.org/abs/1603.02754

主な特徴

• ヒストグラムベースの分割
  連続値特徴量をあらかじめビン（例：256）に分割して高速な分割候補評価を実現。
• 正則化項を含む目的関数
  L1/L2正則化を導入し、モデルの複雑さを抑えて汎化性能を向上。
• DART（Dropout Additive Regression Trees）
  一部の木を無視して学習することで、過学習を抑制するDropout風手法。
• 豊富な並列処理対応
  OpenMPによるマルチスレッド、GPU（CUDA）、Rabit/daskによる分散学習に対応。

欠損値の扱い

• 学習時に「欠損値を左に送るか右に送るか」を両方試し、情報利得が最大の方向を選ぶ。
• この分岐はモデルに記録され、推論時にも同様に自動で処理される。

6.2 LightGBM

LightGBMは、Microsoftが開発した高速・軽量なGBDT実装です。2016年に公開され、XGBoostに比べて学習速度・メモリ効率に優れた性能を持ちます。

https://www.microsoft.com/en-us/research/publication/lightgbm-a-highly-efficient-gradient-boosting-decision-tree/

主な特徴

• Leaf-wise成長戦略
  情報利得が最大の葉ノードを優先的に分割。精度は高いが、木が深く非対称になる傾向がある。
• GOSS（Gradient-based One-Side Sampling）
  勾配の大きいサンプルを優先的に使用し、小さいサンプルを部分的に除外することで高速化と精度の両立を実現。
• EFB（Exclusive Feature Bundling）
  排他的な特徴量をバンドルし、次元削減と計算効率を改善。
• GPU・分散対応が強力
  ヒストグラムベースの分割アルゴリズムとGPU実装の相性が良く、大規模分散学習にも対応。

欠損値の扱い

• 各分割候補において、欠損値を左右どちらに送るかも同時に最適化。
• 欠損値の有無が分岐条件として扱われ、明示的な補完は不要。

6.3 CatBoost

CatBoostは、ロシアの検索エンジンYandexによって開発されたGBDT実装で、特にカテゴリ変数の処理に優れています。

https://arxiv.org/abs/1706.09516

主な特徴

• 順序付きターゲットエンコーディング
  通常のターゲットエンコーディングが持つデータリークの問題を回避するため、学習データの順序に基づいた「逐次エンコード」を採用。
• Oblivious Tree（対称木構造）
  各レベルで全ノードが同一条件で分割されるため、GPUによる高速並列計算が可能。推論速度も高速。
• 自動前処理と安定性
  カテゴリ変数や欠損値の前処理が不要であり、モデルの精度がデータの前処理手法に依存しにくい。
• CPU最適化にも優れる
  リソース制限のある環境下でも安定したパフォーマンスを発揮。

欠損値の扱い

• 欠損値は特別なカテゴリとして扱われ、自動的に処理。
• 分割条件として「欠損あり/なし」も判断材料に含まれ、推論時も自動的に適用。

7. まとめ

本記事では、勾配ブースティング決定木（GBDT）の仕組みや、代表的な実装（XGBoost、LightGBM、CatBoost）の特徴、それぞれの最適化手法や応用可能性について体系的に解説しました。最後にポイントを整理し、GBDTを活用する際の着眼点を振り返ります。

GBDTの強み

• 高い予測精度：単体モデルに比べて高精度であり、実務での信頼性も高い。
• 前処理が比較的容易：スケーリング、正規化、欠損値補完といった前処理がほとんど不要。
• カテゴリ変数・欠損値への対応：特にCatBoostはエンコーディング不要でこれらを処理可能。
• 汎用性が高い：回帰・分類の両タスクに対応可能。

GBDTの限界と課題

• 推論の並列化が困難：弱学習器を逐次的に構築する特性上、学習・推論ともに直列的な処理になりやすい。
• 小バッチ推論に不向き：大量データのバッチ処理には適しているが、1件ずつのリアルタイム推論では遅くなることがある。
• 非構造データへの弱さ：画像、音声、自然言語といった高次元連続データには深層学習が優位。

不均衡データに対する適正

GBDTは、クラスの不均衡がある分類タスクに対しても、以下の理由から比較的高い性能を発揮します。

• 残差に基づく逐次学習：誤差の大きいサンプル（しばしば少数クラスに該当）が強調されやすい。
• サンプルの重み付けが可能：XGBoostのcale_pos_weightなどを用いて、少数クラスの重要度を調整できる。
• 評価指標に合わせた最適化が容易：精度だけでなく、AUC、F1、Loglossなど適切な指標でモデルをチューニング可能。

そのため、不正検知や異常検知などでも、「別途リサンプリングせずにまず試す」 手法として有効です。

おわりに

勾配ブースティングについてまとめてみましたが、想像以上に奥が深く、学ぶことの多いテーマでした。
今後も、利用するアルゴリズムについては仕組みを理解しながら、丁寧に活用していきたいと思います。勉強しながらの執筆なので、もし内容に誤りや分かりづらい点がありましたら、ご指摘いただけると嬉しいです。最後までお読みいただき、ありがとうございました。

参考資料

• https://explained.ai/gradient-boosting/descent.html
• https://randomrealizations.com/posts/how-gradient-boosting-does-gradient-descent/
• https://medium.com/riskified-technology/xgboost-lightgbm-or-catboost-which-boosting-algorithm-should-i-use-e7fda7bb36bc