トポロジカルデータ解析で見る株式市場のトレンド転換点
トポロジカルデータ解析で見るS&P500のトレンド転換点:数学的アプローチによる市場変動の検出
はじめに
昨今のトランプ関税の煽りを受けた株価の暴落を受けて、過去の株価に大きく影響を与えた要素をトレンド転換点の検出によって探し出せないかと考えました。本記事では、従来の技術的分析とは異なるアプローチとして、トポロジカルデータ解析(TDA)を用いた新しい手法を提案します。
前半部分はトポロジカルデータ解析の概要について、後半部分では実装した箇所をコードとともに解説していきます。
1.トポロジカルデータ解析とは
トポロジカルデータ解析とはデータの形状的・位相的特徴を解析する手法の総称であり、特に高次元データやノイズを含むデータに対して有用です。
TDAでは、データの形状や構造を解析するために、
①:点群データをグラフやネットワークのような「単体的複体」に変換
②:スケールに応じて発展させる「フィルトレーション」を行う
トポロジカルデータ解析には、一般的にパーシステントホモロジー法とマッパー法の二つが存在します。今回はパーシステントホモロジー法について解説します
1.1パーシステントホモロジー法

イメージとしては、点を中心に半径rの円を作成します。パラメータrを徐々に大きくしていき、円と円がつながると点線を結びます。その様子を観察します。
- 初期状態:点群のみ(r=0)が存在します。
- パラメータrを大きくしていき、距離がr以下の点同士を結んで線にします。
- さらにrを大きくしていき、3点全てが結ばれた場合、点同士を結んで三角形にします。

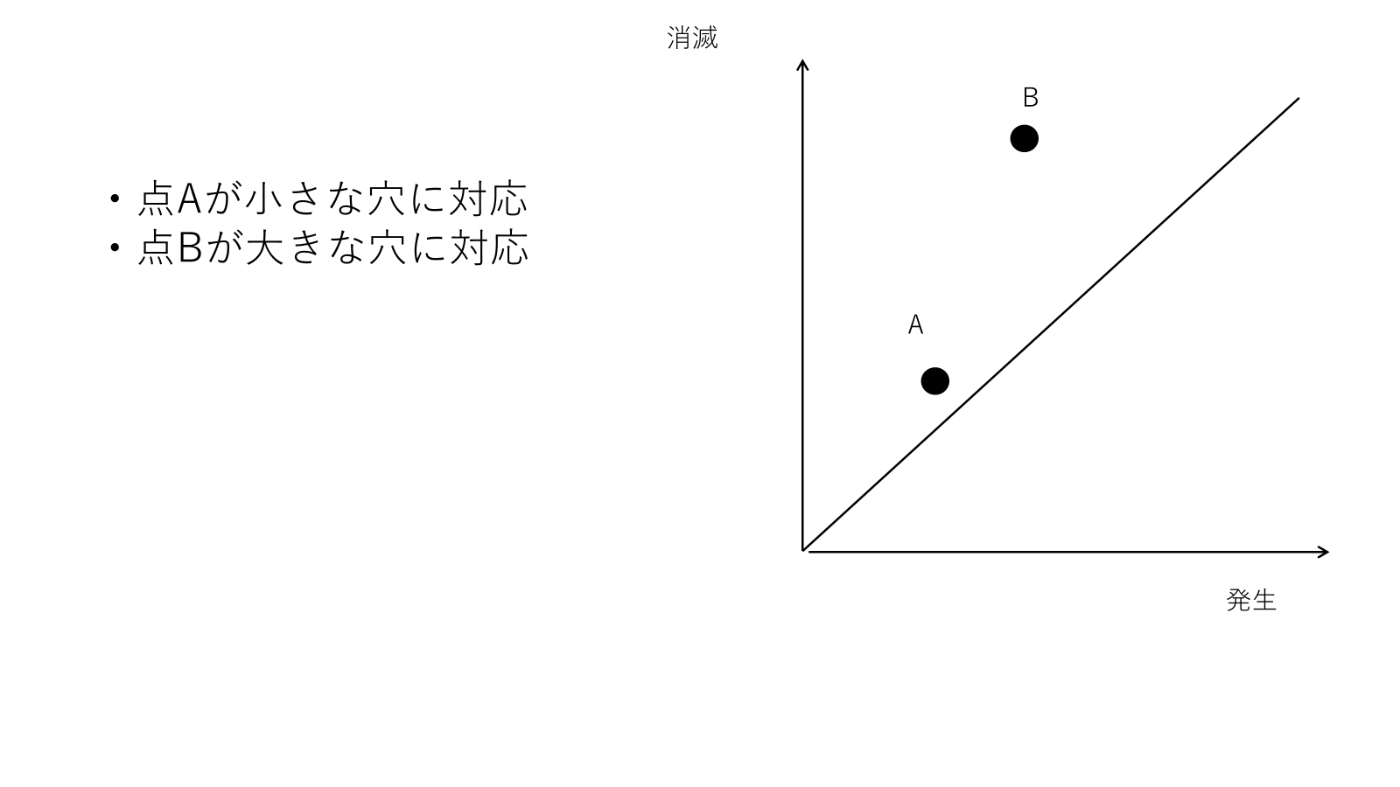
パーシステントホモロジー図
パーシステントホモロジー図は、各トポロジカル特徴の「誕生時のスケール r」と「消滅時のスケール r」を2次元プロットしたものです。対角線に遠い点はノイズ、対角線から近い点は重要なトポロジカル特徴となります。

2.S&P500のトレンド転換点検出
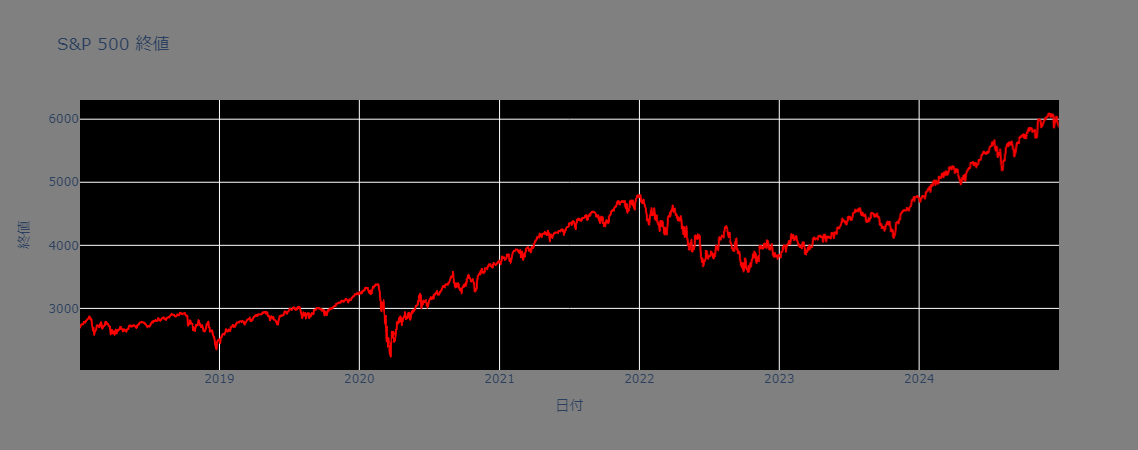
今回検証対象となるのは2018-01-01~2024-12-31の7年間のS&P500のデータになります。
2.1実装環境と必要なライブラリ
本分析で使用するライブラリとバージョンは以下の通りです:
import numpy as np # >= 1.20.0
import pandas as pd # >= 1.3.0
from gtda.time_series import SlidingWindow # >= 0.5.0
from gtda.homology import VietorisRipsPersistence
from sklearn.decomposition import PCA # >= 0.24.0
from sklearn.cluster import KMeans
2.2パラメータ設定の根拠
本分析では以下のパラメータを採用しています:
2.2.1スライディングウィンドウのパラメータ
-
window_size = 50(50営業日)- 約2.5ヶ月分のデータを1つのウィンドウとして扱います
- 一般的な技術分析で使用される移動平均(20日、50日)との整合性を考慮
- より長期(100日)では局所的な変化の検出が困難に
- より短期(20日)ではノイズの影響が大きくなる傾向
-
n_stride = 5(5営業日)- 週単位での変化を捉えるために設定
- より小さい値(1-2日)では計算コストが増大
- より大きい値(10日以上)では重要な変化点を見逃す可能性
2.2.2Vietoris-Rips複体のパラメータ
-
homology_dimensions=[0, 1]- 0次元:連結成分の数(データ点のクラスター)
- 1次元:ループ構造(周期性や循環的パターン)
- 2次元以上は計算コストが高く、解釈が困難なため除外
2.3パーシステントホモロジー図の作成
from gtda.time_series import SlidingWindow
from gtda.homology import VietorisRipsPersistence
from gtda.plotting import plot_diagram
# 数値データのみ抽出(終値のみ使用)
X = df_sp500["Close"].values
# スライディングウィンドウで時系列を埋め込む
window_size = 50 # 50日間の移動窓
n_stride = 5 # 5日ごとに1点を取得
embedder = SlidingWindow(size=window_size, stride=n_stride)
embedded_data = embedder.fit_transform(X.reshape(-1, 1))
- スライドウィンドウ法は、時系列データを一定のサイズ(
window_size)に区切って並べる方法です。-
size=50:各ウィンドウは50個のデータ点を含む(50日分のデータ)
-
stride=5:5日ごとに1つの新しいウィンドウを作成(オーバーラップあり)
-
イメージ(X = [x1, x2, ...,]の場合)
[x1, x2, x3,..., x49, x50] [x6, x7, x8, x9, x10, ..., x54, x55] ... -
Embedded data shape: (343, 50, 1)
-
# Vietoris-Rips 複体を用いた持続ホモロジー
VR = VietorisRipsPersistence(homology_dimensions=[0, 1]) # 0次元と1次元の特徴を抽出
diagrams = VR.fit_transform(embedded_data)
# 位相的特徴の可視化
plot_diagram(diagrams[0])
パーシステントホモロジー図

パーシステントホモロジー図の特徴について詳しく説明します:
2.4パーシステントホモロジーを用いた市場の状態のクラスタリング
2.4.1クラスタリング手法の選択理由
PCAによる次元削減
- パーシステントホモロジー図から得られる特徴量は高次元
- 2次元に圧縮することで、以下の利点:
- 可視化が容易
- クラスタリングの精度向上
- 計算効率の改善
- 累積寄与率:約85%(上位2主成分で情報の大部分を保持)
KMeansクラスタリング(k=2)
- クラスタ数を2に設定した理由:
- 市場状態を「通常期」と「転換期」に分類
- シルエット分析でk=2が最適と判断
- より多くのクラスタでは解釈が複雑化
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
# パーシステンスホモロジー図の特徴を次元削減
persistence_features = VR.fit_transform(embedded_data)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(persistence_features.reshape(len(persistence_features), -1))
# クラスタリング(市場状態を2つに分類)
kmeans = KMeans(n_clusters=2, random_state=42)
labels = kmeans.fit_predict(X_pca)
# クラスタリング結果をデータフレームに格納
df_plot = pd.DataFrame({
"PCA Component 1": X_pca[:, 0],
"PCA Component 2": X_pca[:, 1],
"Cluster": labels
})
# Plotlyで散布図を作成
fig = px.scatter(
df_plot,
x="PCA Component 1",
y="PCA Component 2",
color=df_plot["Cluster"].astype(str),
title="Market Regimes Clustering via TDA",
labels={"Cluster": "Market Regime"},
color_discrete_sequence=px.colors.qualitative.Set1
)
fig.update_layout(plot_bgcolor="black",
paper_bgcolor="grey")
fig.show()

2.4.2クラスタリング結果の解釈
2.5トレンド転換点の可視化と分析
import plotly.graph_objects as go
import pandas as pd
# 日付インデックスをリセットして適切にスライス
df_sp500 = df_sp500.reset_index()
dates = df_sp500["Date"].iloc[window_size:].values
prices = df_sp500["Close"].iloc[window_size:].values
# クラスタリングのラベルに対応するインデックスを取得
trend_change_dates = dates[::n_stride][:len(labels)][labels == 1]
trend_change_prices = prices[::n_stride][:len(labels)][labels == 1]
# Plotlyで可視化
fig = go.Figure()
# 元の株価推移をプロット
fig.add_trace(go.Scatter(
x=dates,
y=prices,
mode="lines",
name="S&P 500",
line=dict(color="blue")
))
# クラスタリング結果に基づく転換点をプロット
fig.add_trace(go.Scatter(
x=trend_change_dates,
y=trend_change_prices,
mode="markers",
name="トレンド転換点",
marker=dict(color="red", size=8, symbol="cross")
))
# グラフのデザイン設定
fig.update_layout(
title="トレンド転換点検出",
xaxis_title="日付",
yaxis_title="終値",
legend_title="Legend",
plot_bgcolor="black",
paper_bgcolor="grey"
)
fig.show()
# fig.write_image("トレンド転換点.svg")
fig.write_html("トレンド転換点.html")

2.6結果の分析と考察
結果を確認してみると、2020年前半、2022年、2024の始め、2024年の終わりにトレンド転換点が凝集していることがわかりました。背景には、いくつかの重要な経済・政治的イベントが起きていることがわかりました。
📅 2020年(大統領選挙年)
- S&P500のトレンド転換:急落(2〜3月)→ 急上昇(4月以降)
-
主な要因:
- 新型コロナウイルスの世界的パンデミックによる市場暴落。
- FRBのゼロ金利政策、量的緩和、米政府による巨額の財政出動(CARES法)。
- 11月:バイデン vs. トランプの大統領選挙。政権交代期待と不透明感が交錯。
-
関連トピック:
- 米中関係の緊張(関税戦争の延長線)。
- テック株の爆発的成長(在宅需要)。
📅 2022年(中間選挙年)
- S&P500のトレンド転換:年初から大きく下落 → 年末にかけて反発傾向
-
主な要因:
- 高インフレ(40年ぶりの水準)とそれに対するFRBの急激な利上げ(0.75%連発)。
- 景気後退懸念、企業業績の悪化。
- 11月:中間選挙(バイデン政権2年目)。議会の勢力バランス変化が政策見通しに影響。
-
関連トピック:
- ロシアによるウクライナ侵攻(2022年2月)→ 原油・エネルギー価格高騰。
- 世界的なサプライチェーンの混乱。
📅 2024年(大統領選挙年)
- S&P500のトレンド転換:年始に上昇→途中調整→年末に再び動意(想定)
-
主な要因:
- 金融政策の転換点(FRBが利下げに転じる可能性)。
- インフレ収束傾向と景気回復の兆し。
- 11月:大統領選挙(バイデン再選か、共和党候補による政権交代か)。
-
関連トピック:
- AI・半導体関連銘柄のバリュエーション拡大。
- 米中テクノロジー戦争の新展開。
- 中東や台湾情勢など、地政学リスクの高まり。
🔁 まとめ:トレンド転換要因

- 選挙サイクル:大統領選挙年と中間選挙年は、政策の不確実性・期待感の増減により市場が転換しやすい。
- 金融政策:FRBの金利の方向性が市場のトレンドに大きく影響。
- 地政学リスク・エネルギー価格:特にロシア、台湾、中東関連の出来事は大きな市場インパクト。
- イノベーションの波:パンデミック時のテック株、2024年のAIブームなどが局所的なラリーや下落を引き起こす。
2.7手法の限界と注意点
2.7.1検出精度に影響する要因
-
ウィンドウサイズの選択
- 大きすぎる:微細な変化を見逃す
- 小さすぎる:ノイズを拾いすぎる
-
データの質
- 取引量の少ない期間での信頼性低下
- 異常値の影響を受けやすい
-
計算上の制約
- リアルタイム処理には不向き
- 大規模データセットでの計算コスト増大
2.7.2改善の可能性
- アダプティブウィンドウサイズの導入
- マルチスケール解析の適用
- 並列計算による処理速度の向上
Discussion